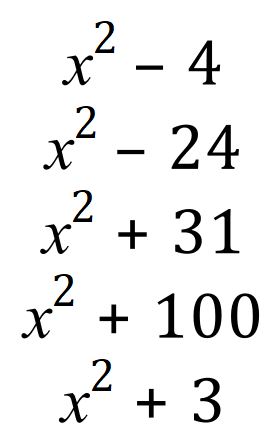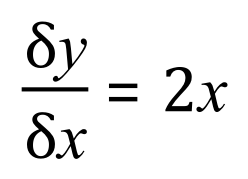[A] The Power Rule
As we have discussed above, the reverse of differentiation is integration, or producing the anti-derivative from the derivative, in which case the anti-derivative of 2x is x2 . Well, this is all well and good, but how do we get there? What rule do we apply to the derivative to get its anti-derivative, or integral?
The answer is quite simple:
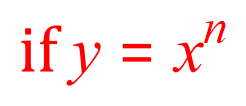
Then the antiderivative is .....
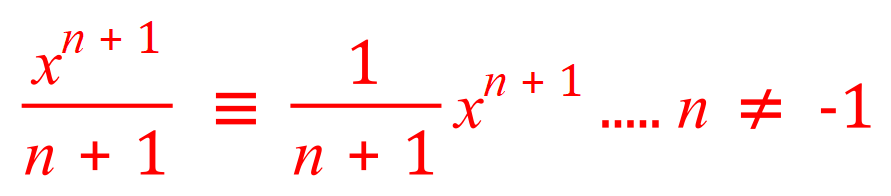
This is known as the "Power Rule".
I’ve written the result in two different ways, because depending the text you read you may see it expressed in either way, and indeed in some texts interchangeably.
There is a special symbol to represent the integral, or anti-derivative which looks like a stretched S (it is said that this comes from the word sum, because integration deals with calculating the area underneath the curve and one of the simplest ways to approximate this is to divide the area into long strips and total their individual areas, that is to take the “sum” of the individual areas of the strips that make up the whole).
In which case:
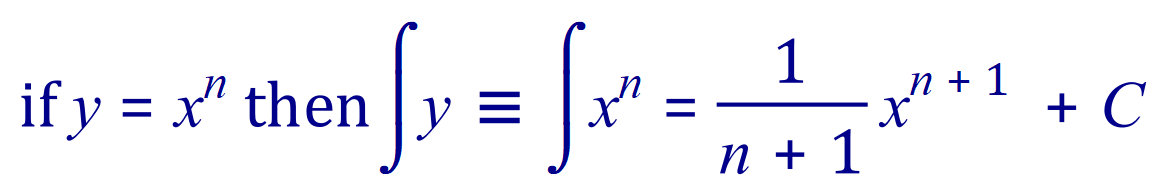
You will probably have noticed that I’ve introduced another object, C, which is known as the “constant of integration”. Let me explain it by taking an actual example:
|
|
If we differentiate all five of these functions of ‘x’ we arrive at the same answer every time…….
Look back at the section on differentiation if you can’t see why this is the case, but if you differentiate a constant it disappears so in each of the five cases above the derivative will be the same. Can you see the problem here? The problem is, if we choose to integrate back to one of our functions, we simply can’t do it and hope that we arrive back at the exact expression that we differentiated to start with. The anti-derivative of 2x can be any one of them, and an infinite number of others beside. The truth is the constant was differentiated out but when we integrate it has to come back but we don’t know what value it was to start with! To take this into account we use the arbitrary constant ‘C’ to represent the constant value irrespective of what it was. |
You will find when you become practised in indefinite integration (that is integration of a function where no limits of integration have been applied) that you will automatically quote your answer inclusive of the constant of integration.
Go To >> Table Of Standard Derivatives And Integrals <<