Newton's Second Law
We now come to Newton's second law. Newton's second law states that an object's acceleration is directly proportional to the resultant force acting on it and inversely proportional to its mass. There is a simple and straightforward mathematical relationship which exemplifies this:
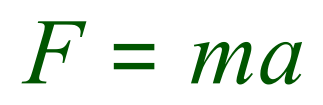
Where:
- F is the resultant force and measured in Newtons (N)
- m is the mass of the object measured in kilograms (Kg)
- a is the acceleration measured in metres per second per second (m/s2)
Note that we are talking about the resultant forces, and not necessarily the applied forces. What this means is if a force of a certain magnitude is being applied, but an opposing force of a slightly lower magnitude is resisting, then it will be the difference (the resultant) that would be used in any calculation involving the above formula. Let's take a look at a quick example just to make that clear.
Q. A car with a mass of 1250 kg has an engine that provides a driving force of 5200 N. At 70 miles an hour the drag force acting on the card is 5100 N. Find the acceleration of the car at 70 miles an hour.
This is a very interesting question because we are given a speed/velocity of 70 miles an hour which you would automatically be inclined to try to convert to m/s. As this particular piece of information is redundant (something which you will really find in question) there is no need to convert it because it is not going to be used anywhere. As I said it is the "resultant" force which needs to be considered which is the difference between the applied force and the opposing/resisting force.
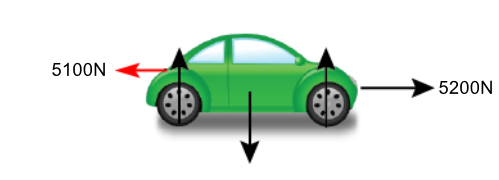
Let's take a look at our little green car once more. The driving force (which pushes the car forward) is 5200 N and the drag force which is trying to hold the car back (friction/air resistance and so forth) is 5100 N, so the resultant force is the difference between the two which is 100 N.
However, we still are not ready to make the calculation because the formula/equation needs to be rearranged in terms of the quantity which we wish to calculate, that is acceleration:
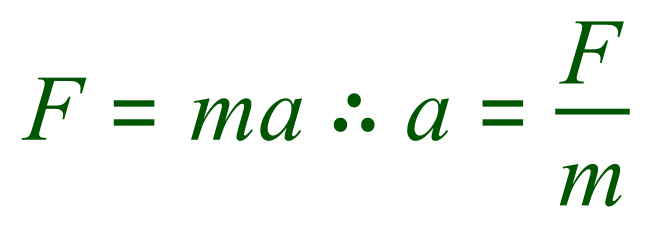
Substituting our values into the equation now:
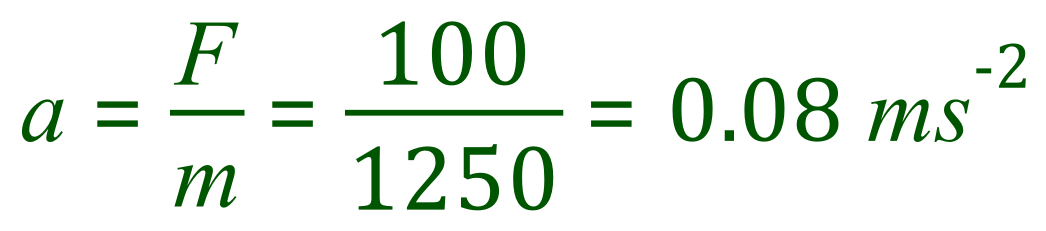
Back To >> Changes In Momentum <<
>> Questions <<