Percentages

When we see the word "percentage" or "percent" we understand that there will be a number followed by the % sign. For example 33%, 25%, 10% and so on. What does this mean though?

Break the word down into two pieces:

Percent = "Per" + "cent" which simply means "Per" 100, or a number out of, or "from" every 100.

Starting off simply, if we have 100 items, this could be anything, bananas, marbles, cars, bottles, what ever you wish, and we remove, say, 10 percent, what we are actually doing is removing 10 items for every 100 that we have. So removing 10 out of every 100 is removing 10 percent, written 10%.

Q. What happens if we remove 10% of 200 items?

A. First of all, ask yourself how many 100's we have. You should be able to see that we have 2 (100's) so if we remove 10 items from every 100, we end up removing 20 items from the whole 200, that means that 20 is 10% of 200.

Q. What about if we have 400 items, and we remove 15 percent of them ?

A. Well, how many 100's do we have ? - answer is that we have 4 (100's) and from each 100 we take away 15. So, if we do this for every 100, we end up removing 4 x 15 = 60. We can say that 60 is 15% of 400.

To really get to grips with percentages, we need to push this idea just a little bit further, and look at changing the percentage number itself into a fractional form. Think again about 10% and that we said it was "10 out of every 100", can you see that another way of saying "10 out of every 100" would be "ten hundredths" or 10/100 ?

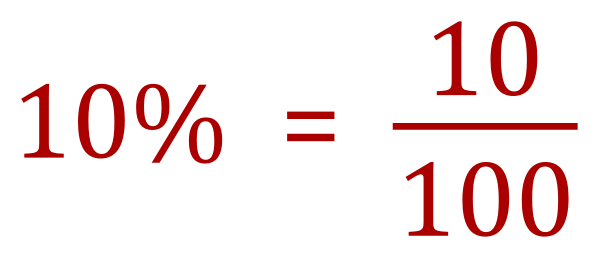
So we can also say that 15% would be 15/100:

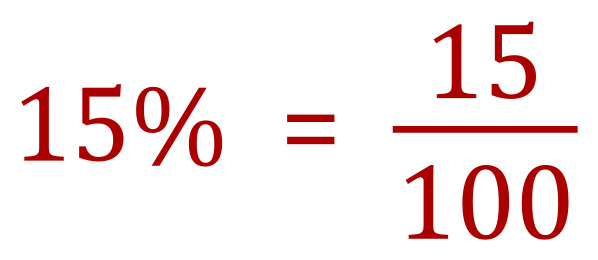
Also 40% would be 40/100:

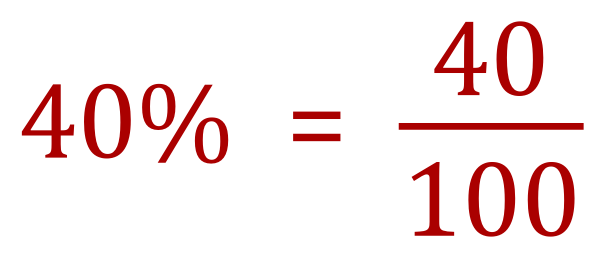
Now, sometimes it is easier to use a letter to represent the number that is being changed. We call this "algebra" and although it appears a bit weird to start with, you will find that in maths it is done quite a lot. Numbers that keep changing in value are called "variables" and because of this it is much easier to give them a letter rather than trying to give them fixed number every time, it just doesn't work.

With this in mind, let us call our percentage 'x', so for each instance of 10, 15 and 40 that we have used previously, let us simply replace this number with 'x'

This is a completely different representation, but it is quite simple, we can now restate our little equation above like this:

Stop and think about this for a while, look at the previous 3 equations where we used 10, 15 and 40 and notice that they have been replaced by the single letter 'x'. Much simpler, wouldn't you agree?

Okay, we now understand that 'x' percent is "'x' hundredths" but we need to know what it is a percentage of. We said that 15% would be 15 out of every 100 and that if we had more than 1 x (100's) we would multiply 15 by the number of hundreds that we actually had, so restating the example above where we actually had 4 x (100's) we simply multiply 15 x 4 and arrive at 60 as you saw before.

Now we need to look at the expression "so many percent of" and find out exactly what the word "of" represents in mathematics. When we use the word "of" in this context we are using "times" so if I was to say "15 of 3" what I would be saying is that I have 15 lots of 3 items, which is 15×3 or 45 in total.

Taking this one step further we say that 15% is therefore "15 hundredths of"

In one of our fractions above we actually saw that 15% was the same as 15 hundredths, but let's now put it into context by using it and let us work out what 15 hundredths of 100 is:

If you're quite sharp with your maths you will see straight away from this equation that the two 100s will cancel out leaving you just 15. In other words you have worked out that 15% of 100 is in fact 15. Of course things aren't always that simple, so let's go back to our previous example where we said 15% of 400:

Q. What about if we have 400 items, and we remove 15 percent of them ?

I have repeated the question from above and coloured it purple just for easy reference but what we need to do now is restate the question using purely numbers. So 15% of 400 items, written as one of our expressions would be:

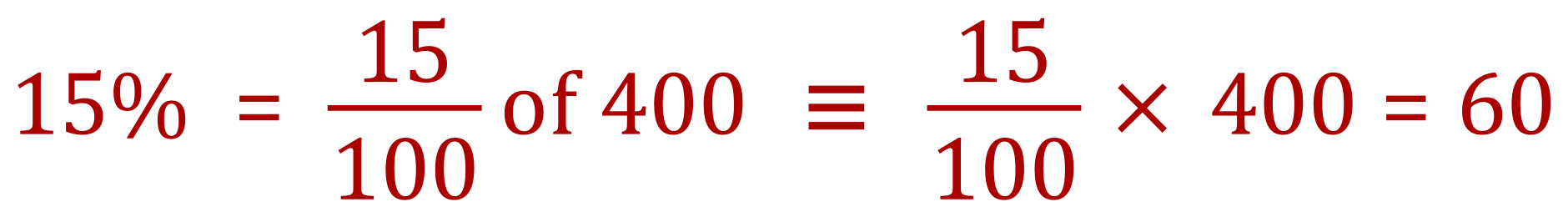
And how we actually calculate this is by multiplying the percentage (in this case 15) by the number of items (in this case 400) and then divide the result of that by 100 to return it as a number of items.

Q. Work out 20% of 200

A. 20% of 200 is 20/100 * 200 = 40

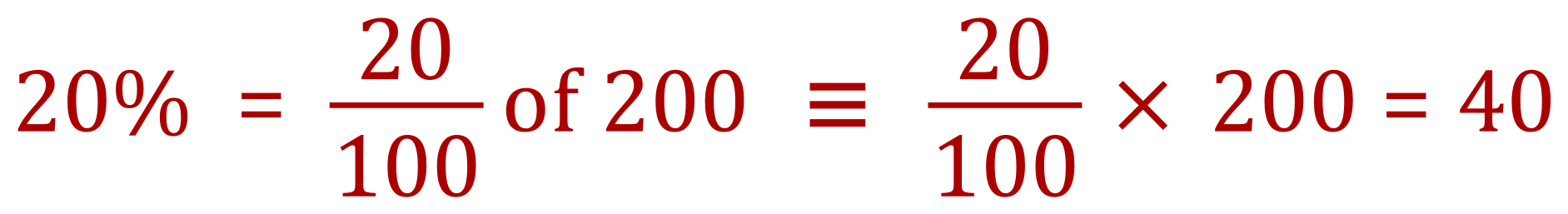
Notice that to work this out we multiplied the percentage (20) by the number of items (200) which would have given an answer 4000 and then we divided this by a hundred giving us the final answer of 40 so 20% of 200 is indeed 40.

I said earlier that using letters instead of numbers that keep changing can sometimes be the better option, we replaced our percentage with 'x' and so now will replace the number of items with 'y' to give us a single general expression for percentage:

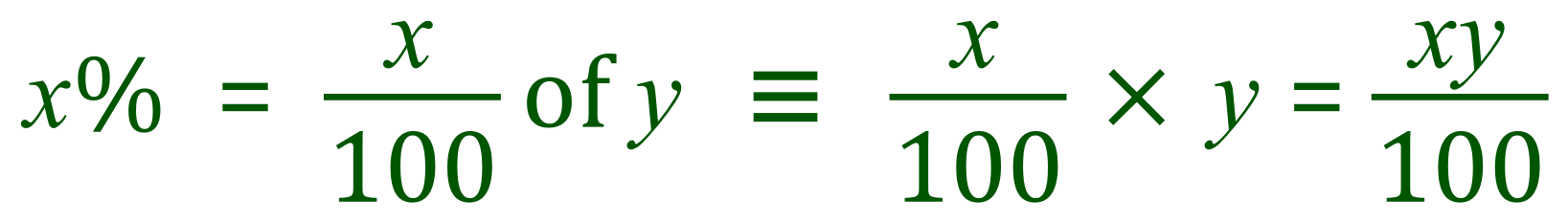
This will probably make a lot more sense when you do some more examples of it, but if you consider the percentage that you want as 'x' and the number that you want the percentage from as 'y' then it becomes apparent that you are multiplying 'x' and 'y' together and dividing the result by 100.