Ratio and Proportion
Consider making a cake. You may need to add half a kilogram of flour (500 g), 200 g of sugar, 3 eggs, 200 g of butter or margarine and so on. What this cake would taste like I have no idea, I have simply made up these amounts to give you an idea of "proportion". For example you can see that you would use more flour than sugar, about the same amount of butter or margarine as sugar and any decent cookbook would give you the correct weights.
If you follow the instructions carefully, there is no reason why you can't come out with a very nice cake.
Now consider building a brick wall (hopefully not with all of your remaining cakes). To make the cement/concrete mix you would probably mix cement powder and building sand in a proportion whereby you use 3 times more sand than cement. Notice this time that weights haven't been given, because cement/concrete mix is a bulk item and it could be that tons and tons of it need to be made for various things so be quite strange to start apportioning things by weight.

Once again we look at "proportion".
A suitable "definition" of ratio is that these are items/variables used to compare quantities. So going back to our building cement we might say that for every "unit amount" of cement powder we would need to add 3 units of builder's sand, so the proportion of cement to sand would be 1 to 3.
When we are comparing proportions, for example "x to y" we express this as a ratio of one component to another.
Going back to our concrete mix we would say that the ratio of cement to sand is "one to three" which would be written 1:3. It does not matter which way around the numbers are written, provided that the numbers refer to the correct items. You will notice in questions on ratio and proportion that the items will be given in a specific order, and this is the order that the numerical values must also follow.
Example:
As we have said above, to make cement/concrete mix (we usually call this mortar) we mix sand and cement together in a ratio of 3:1. You can see by the simple sentence above that Sand = 3 and Cement = 1, not the other way around.
Ratio and proportion doesn't stop at just 2 items, we can have ratios of 3, 4, 5 and so on items and it should be clear from the question you are being asked what the items are and the order.
Example:
Q. Write down each of the following ratios in their simplest form:
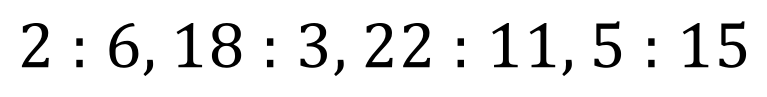
A. The answers are:

In all cases, a ratio should be reduced to its simplest form wherever possible. If a ratio involves a prime number it is likely that you will not be able to simplify very much, if at all.
As is the case in almost every area of mathematics, you won't necessarily just be given numbers to deal with. You may be given a short written scenario from which you have to work out what you're being asked to do, and then perform the calculations to do it.
Example:
Q. In your mathematics class there is a total of 33 students, 15 of which are girls. Write down the ratio of boys to girls in the class, in its simplest form.
A. You are given 2 pieces of information, the total number of students (33) and the number of girls (15) so you should be able to quickly work out that there are 33-15=18 boys in class. We can now write down the ratio of boys to girls is 18 to 15:

How do we actually simplify this? Well, we have to look for the largest number that divides into both numbers in the ratio. Working through the factors of 15 and 18:
15 = 1, 3, 5
18= 1, 2, 3, 6, 9
You should be able to see that the highest common factor is 3, in which case we divide both numbers and the ratio by 3.
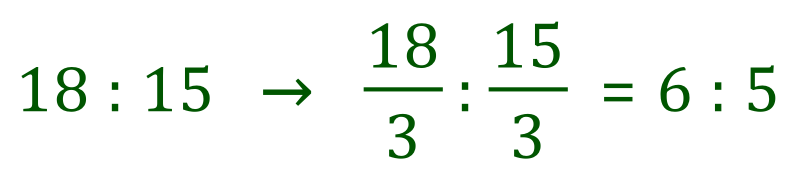
With therefore state that "the ratio of boys to girls in the class is 6:5"
Another thing that might trip you up is if you are given differing units in the ratio. The first thing that you have to do is convert all of the values concerned to the same unit, before you can produce the ratio.
Q. Write down the ratio 3.6 m to 12 cm in its simplest form.
A. We must convert our values to the same units, obviously in this case we will need to convert metres into centimetres, so 3.6 m becomes 360 cm. Now we can make the comparison and reduce the ratio to its simplest form.

You can if you wish write out all of the factors of 360 and 12, and choose the highest common factor (in this case it would be 12) but it is likely you could see from inspection that 12 divides into 360 exactly 30 times (12 divides into 36 (3 times), then multiply the answer by 10).
>> Questions <<