Sound Waves
Q1. A musical instrument produces a sound wave with a wavelength of 0.66 m and a speed of 300 m/s in air. The sound wave enters water whereupon its velocity changes to 1500 m/s. Calculate the new wavelength of the sound wave.
A1. We know that when a sound wave enters a denser medium, its velocity increases however the frequency of the sound wave does not change. This means that the wavelength must also increase given the standard velocity / frequency / wavelength relationship:
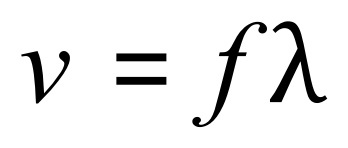
From the information we have, we do not as yet have a value for the frequency. This is what we need to find out first:
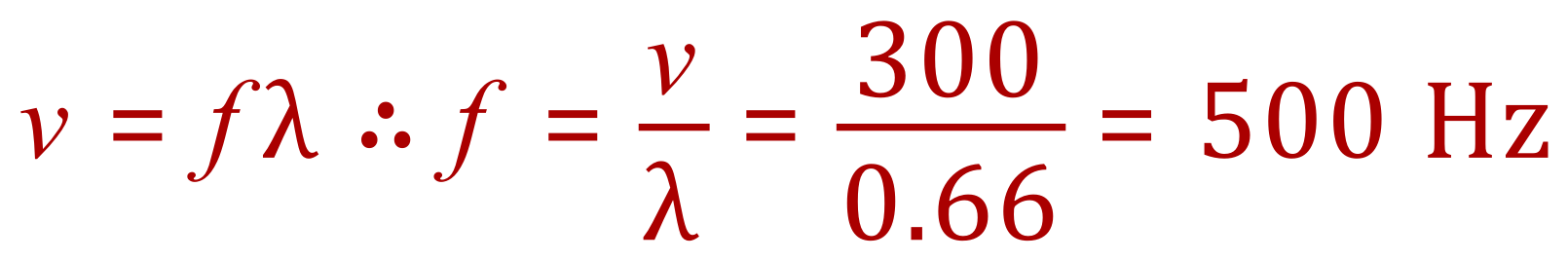
Having established the frequency, and knowing that this does not change, we can now calculate the new wavelength of the wave given the fact that the velocity increases:
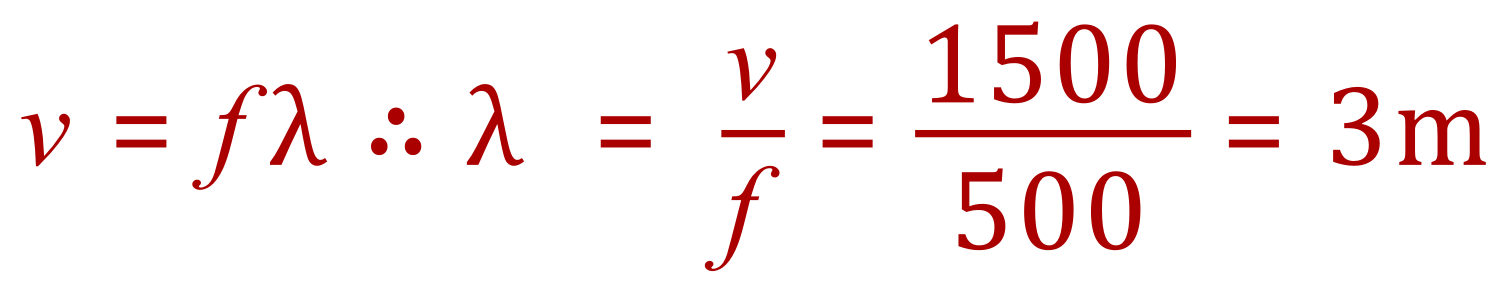
Q2. A sound wave with a wavelength of 3.3 m travels through concrete at 3300 m/s. When the sound wave leaves the concrete it passes into a steel beam whereupon it wavelength increases to 6 m. From this information calculate the speed of the sound wave as it is passing through the steel beam.
A2. First of all, consider the concrete. We know the wavelength and velocity, what we don't know is the frequency which we will now evaluate:
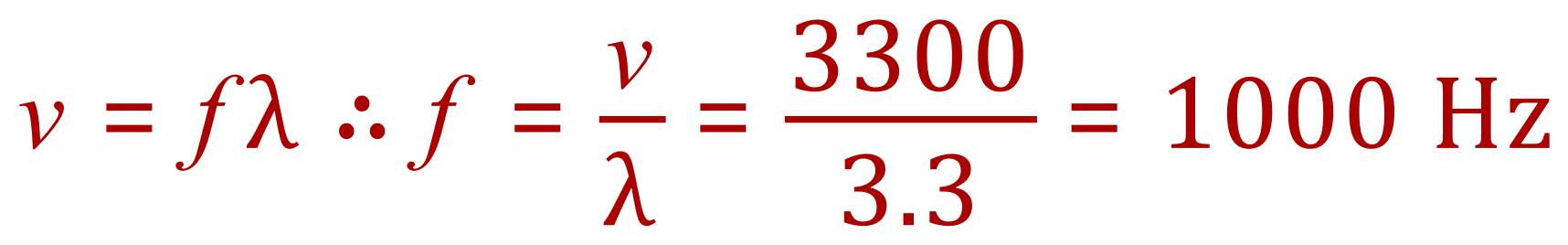
We also know that the frequency of the wave will not change, but we are told that when it enters the steel, the wavelength increases to 6 m. From this we can calculate the new velocity:

Q3. A musical instrument produces a sound wave with a frequency of 1000 Hz. The sound wave has a wavelength of 0.34 m in air. Calculate the speed of the sound wave in air.
A3.

Q4. In water the speed of sound is different. The speed of a sound wave in water is 1300 m/s. The sound wave has a frequency of 1000Hz. Calculate the wavelength of this sound wave.
A4.
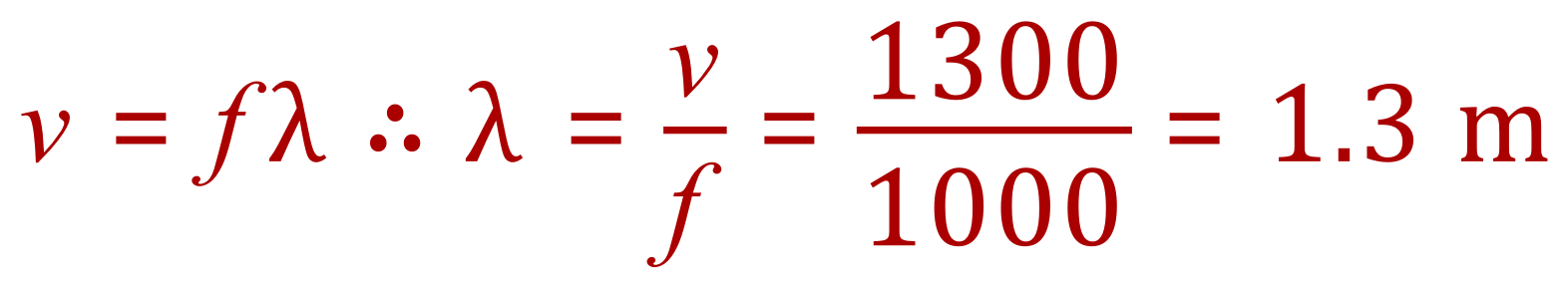
Q5. The diagram shows a ship using an Echo locator (SONAR) to find a submarine. The pulsed wave is transmitted from the ship, which is then reflected off the top of the sub and is then picked up by the receiver.
Given that the speed of sound in water is 1300 m/s and the frequency of the SONAR pulse is set at 500 Hz, what is the depth of the submarine if the pulse "round trip" is 0.2s ?
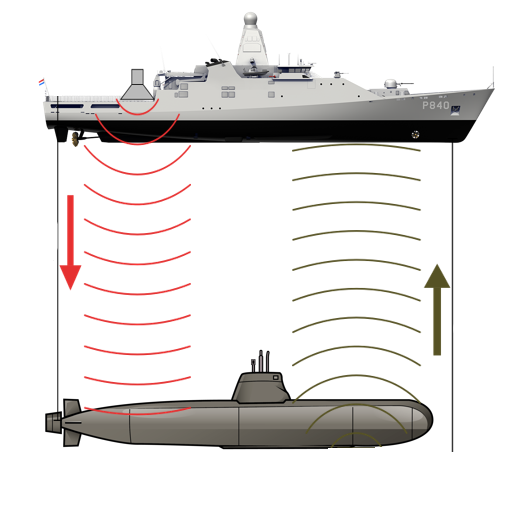
A5. You may think that we need to calculate the wavelength of the SONAR pulse? We are told that the speed of sound/velocity of sound in seawater is 1300 m/s and that the frequency of the pulse is 500 Hz.
There is a little bit of redundant information in this question, because we only need the speed of sound, we do not need to use the frequency or the wavelength as this is a simple instance of the familiar speed equals distance over time equation:

There are a couple of valid points to consider here, first of all you are given a round trip time of 0.2 seconds so the time that you are actually interested is 0.1 seconds (the time it takes for the SONAR pulse to reach the submarine)
Secondly, you may be expected to be able to recall other equations and aspects of the physics you've learnt. We are talking in this section about waves and the familiar velocity / frequency / wavelength relationship but the questions do not have to confine their expectations to this, you need to be flexible in your thought processes.
Back To >> Questions <<
Back To >> Sound Waves <<