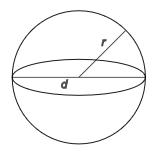
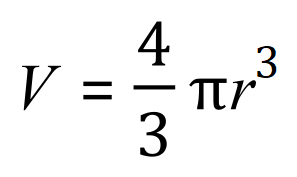Spheres
When we start to look at Spheres, we are looking at “circles in 3 dimensions”. The formulae involved for calculating the volume and surface area of a sphere can be established mathematically, but it is quite complicated to do it. We will simply accept the formulae as given and use them as “plug-ins” as before.
|
|
|
|
|
Q. Calculate the volume of a football which has a regulation diameter of 22 cm.
You’re given the diameter, so you should be able to work out straight away that the radius is 11 cm. If you don’t understand where this came from, look back at previous parts of this document. Now that we’ve established a value for the radius, it is just a matter of “plugging in” all the numbers that we have to come up with a volume.
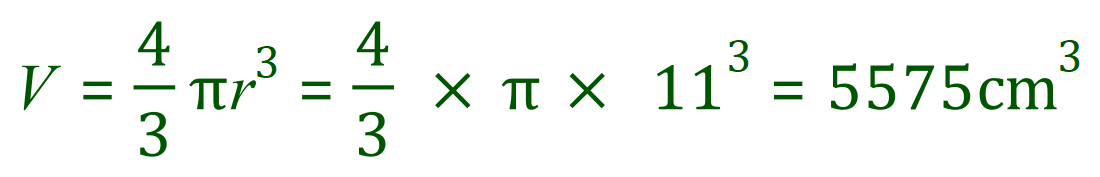
You could also be given a value for the volume of a sphere, and be asked to establish its diameter or radius. Let’s take the previous example and “reverse engineer it” to get the radius. This requires you to know how to make the radius the subject of the formula, and this can take some practice.
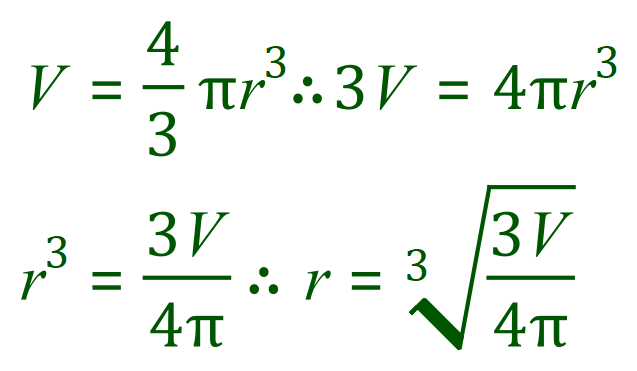
If you’re not sure where this came from, it might be a good idea at this point to stop and study it and follow the steps through for yourself. Only carry on when you’re happy that you understand where the expression for the radius came from.
Plugging in our known values:
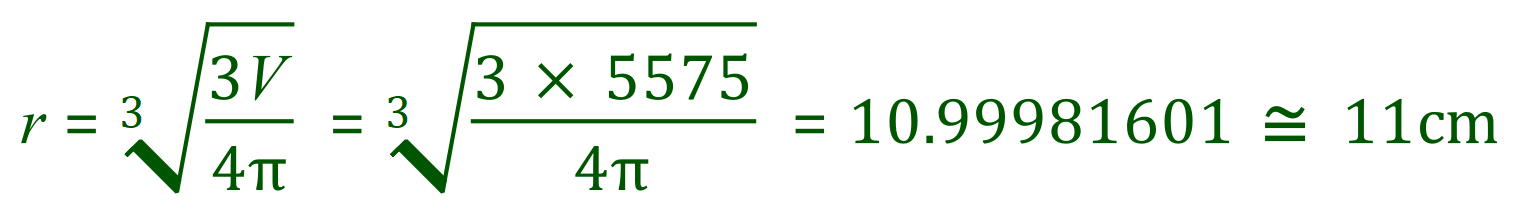
Using pi to around 9 decimal places which the computer is likely to do, gives an answer to a long set of decimal places, but I’m sure you can see that 11 is the logical conclusion.
So, what would be the surface area of a regulation football? Well this is quite simple; we know that the radius is 11 cm and so all we have to do is plug that into the equation for the surface area which is a little bit simpler than the one for volume:
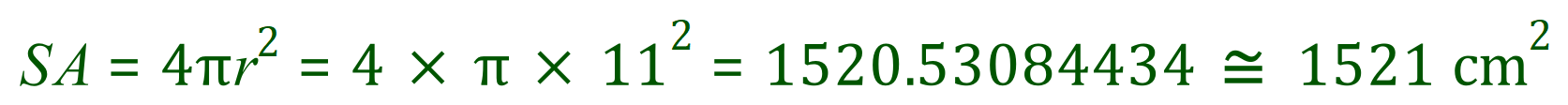
Once again, and I cannot stress it strongly enough, remember your units!
>> Questions <<