Square Numbers
Q. Alice goes swimming once every 21 days whilst Bob only go swimming once every 35 days. They both went swimming today. Use prime factors to find the number of days it will be until they both go swimming again on the same day.
A. The first step in this question is to "prime factorise" both 21 and 35.
21 is simply 3×7 and 35 is 5×7. We need to look at the highest power of each prime factor that appears in either list and multiply these together to arrive at a conclusion. The highest powers that appear are 31 51 and 71 and we multiply these together to make 105. So the number of days it will be before Alice and Bob swim together again will be 105. What we are actually looking at is finding the lowest common multiple of 21 and 35 which is of course 105.
Q. Ben changes the ink in his printer every 216 days whereas Jerry has to change the ink in his printer every 188 days because he uses it more. Both Ben and Jerry visited the local computer shop today and bought brand-new cartridges for their printers. Use prime factors to find out the number of days it will be before they both have to revisit the computer shop on the same day.
A. The prime factors of 216 are 23 x 33 and the prime factors of 188 are 22 x 47. The lowest common multiple, that is the factors that appear in both lists are 23 33 and 47, if we multiply these out we arrive at 10152 which means that Ben and Jerry will not need to go to the printer shop together for a very long time!
Q. Use prime factors to find a pair of numbers that have a highest common factor of 12 and a lowest common multiple of 120.
A. If we establish the prime factors of 12 we come back with 2×2×3. If we then established a prime factors of 120 we come back with 2×2×2×3×5. We then group the sets of numbers according to the commonalities and differences:
(2 x 2 x 3) and (2 x 2 x 2 x 3 x 5) - both sets of numbers have 2×2×3 in common, so let us take this out and we are left with (2 x 2 x 3) and (2 x 5) which gives us a lowest common multiple of 120 and a highest common factor of 12.
The given numbers of 12 and 120 in the above question can be quoted as the answer, but there is also another pair of numbers which can be used to satisfy the question. These are 24 and 60, but how do we get to these?
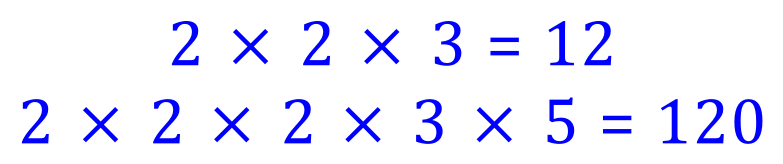
Look at the 2 rows, the top row has the prime factors of 2 and 3 respectively and the bottom row has the same but including 5. There are 2 instances of 2 in the top row and 3 instances of 2 in the bottom row. There is one instance of 5 in the bottom row but there are no instances of 5 in the top row. We can consider 5 as a multiplier or a divisor because 120÷5 gives us 24, and 12x5 gives us 60. Similarly we can consider 2 because there are 3 instances of 2 in the 2nd row, So if we multiply the top row by 2 and divide the bottom row by 2 we arrive at 24 and 60 respectively.
Q. Use prime factors to find a pair of numbers with a highest common factor of 20 and a lowest common multiple of 300
A. Again, we establish the prime factors of both numbers 20 and 300 which is (2×2×5) and (2×2×3×5×5). Our highest common factor is 2×2×5 which is 20 and the lowest common multiple 300. These could be our 2 numbers, alternatively we could have 60 and 100.
Let us take a look at the last answer in more detail:
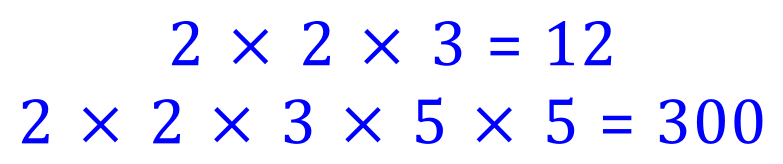
We can see where our first given pair of numbers came from, but I also stated that we could have 60 and 100, where do these come from? If we multiply the top row by 3 using a prime factor from the bottom row, and then divide the bottom row by the same number we arrive at 60 and 100. Both of these numbers also satisfy the requirements of the question.
Back To >> Questions <<
Back To >> Square Numbers <<