Square Roots – Working Out Longhand
This section has talked about square roots, and how they should be used in preference to attempting to give a finite numerical result to an essentially infinite/irrational number. What we haven’t done is explain what a square root is and how to work them out.
We all know what a square root is, but just in case you need a reminder, this is my attempt at explaining what a square root is:
The square root of any number is that number, which, when
multiplied by itself gives the original number.
To make this a little bit clearer, let’s take a look at an example:
the square root of 81 is 9, because 9 multiplied by itself gives 81
the square root of 64 is 8, because 8 multiplied by itself gives 64
the square root of 49 is 7, because 7 multiplied by itself gives 49
the square root of 15,625 is 125, because 125 multiplied by itself gives 15,625
And so on, and so on…
Even when calculators were first conceived, many models automatically included a square root button which would allow you to enter a number and then immediately find it square root by pressing just one button.
This section is going to assume that your calculator is pretty ancient, and doesn’t even include a square root key (just for the purposes of this experiment, your calculator only has the basic 4 functions) and you’re going to have to do it the old-fashioned way!
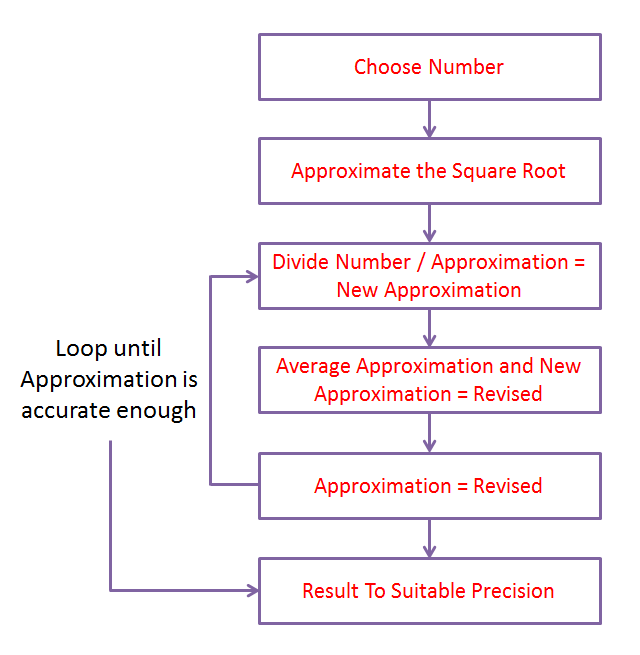
So, how do we work out a square root on paper? Well, there are a number of different ways and some are more complicated than others. I’m going to take you through a method now which I considered to be one of the simpler ones, by going through a couple of examples and then I will give you a flowchart which will hopefully make the process a little bit clearer.
Our first example will be an easy one which will lead to an exact root.
Example 1 - what is the square root of 256?
I should mention at this point that the suffix ‘2’ to the left of the square root symbol simply serves to reinforce the fact that we are looking at square roots, not cube roots or 4th roots or 5th roots or so on but generally for square roots (only) the suffix is omitted.
So let’s go back to the problem, what is in fact the square root of 256?
Step 1 - make an educated guess, we know for example that 10×10 is 100 so the square root of 100 is 10 and we know that the square root of 400 is 20 because 20×20=400 so, because 400 is above 256 and 100 is below it our educated guess must lie between 10 and 20.
Okay, let’s say 15:
Step 2 - we must now divide 15 into 256. If you go back to the section on long division you will see the full method on how to do the above division (that is 15 into 256). For the sake of simplicity I will show the completed stages here.

We can see from the calculation that the numbers shown between the 2 blue horizontal lines, 100 and 90 are going to repeat infinitely, therefore the 6 in the answer will repeat indefinitely, our answer is therefore 17.06666….
Let us now take our answer to be 17.07
Step 3 - add 17.07 to our original guess of 15, take the average which is 16.035 and proceed to step 4.
Step 4 - we now divide 16.035 into 256, using the long division method as shown above, the answer is 15.97 which we add to our previous results of 16.035 making a total of 32.005, which when divided by 2 gives a result of 16.0025.
Step 5 - we now add 16.0025 to 16.035 making a total of 32.0375, the average of the 2 this time is 16.01875
Step 6 - now we add 16.01875 to 16.0025 making a total of 32.02125, when we average the first two numbers we come to a result of 16.01625.
You will notice that the more steps we take, and the more averages of the results we take, our answer is starting to slowly converge towards the number 16. In fact the square root of 256 is 16 so we can in fact stop at this point, only because we know the answer anyway which can be checked with the calculator. You could carry on with steps 7, 8, 9, 10 and so on and each time your approximation would be “16 point something” where the something is rapidly converging towards 0.
To prove the real value of this method however, we need to use a number with an irrational square root, such as for example the square root of 2, the square root of 6, the square root of 17, the square root of 29 and so on, in other words the square root which does not become exact such as in the case of 4, 9, 16, 25, 36 and so on. For our next example we will use such a number.
Example 2 - what is the square root of 91?
Before long, you will become so adept in mental arithmetic that you will know perhaps the first 10 - 20 squares/square roots and as a result you will automatically be aware of an approximate answer to this question before we even put pen to paper. We know that the square root of 81 is 9, and that the square root of 100 is 10. Because 91 lies between 81 and 100 we know that the square root is going to be “9 point something”. Let us implement the method and approximate the square root of 91 to, say, 3 decimal places.
Step 1 - make our first educated guess, for this we will in fact use 9. Now we perform our first “long division”:

Remember that this is our first estimate, clearly our square root isn’t going to be “10 point something” purely because 10×10 is 100. Don’t forget that the number above, 10.111 recurring is purely a second estimate which has to be added to the first estimate and then averaged (that is divided by 2, as per the method).
Step 2 - add 10.111 to 9 and take the average, that is divide the result by 2, giving you an answer of 9.5555 exactly.
Step 3 - divide 9.5555 into 91 giving a result of 9.5233111820417560567212600073256 which we then add to 9.5555, and once again divide the result by 2 this time giving us a result of 9.5394055910208780283606300036628.
I’m going to stop at this point because I’m quoting numbers now at full calculator accuracy, remembering that I can do this because my calculator allows it, it is only the square root key if you remember that isn’t there :-)
Working to full calculator accuracy is always advised, but these numbers are getting quite big and consequently they could become quite unwieldy. Looking at the last 2 rather large numbers you can see that to one decimal place they are the same at 9.5, and it is probable that for the sake of square roots any question you are asked to do could only require you to take the matter to one decimal place (depending on what you are intending to use the result for of course).
If you carried on calculating the square root of 91 you will end up with a number:
9.53939201416946
Which to a reasonable amount of accuracy would be 9.539 and if you multiply this number by itself you will return back to a very close approximation to 91 (in fact 90.992521).
It is highly unlikely that you would ever end up with the calculator in this day and age that could not calculate square roots, but it’s always nice to know how to do these things.
The picture below shows the working screen of a small Visual Basic application that I put together to automate the algorithm above and below it I have drawn a flowchart outlining the steps to take.
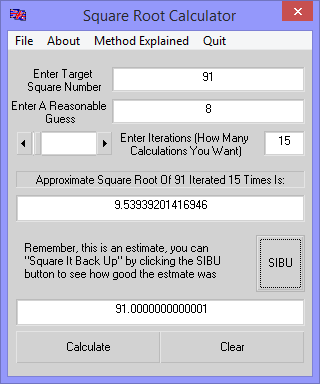
If you study the screen you can see that I’ve worked at the square root of 91 using a 1st guess of 8 (which isn’t particularly reasonable because the square of 8 is 64, which is nowhere near 91, but with this calculation it doesn’t really matter). Where it says “iterated 15 times” this tells you have taken the approximate answer, added it to the previous guess, divided that total by 2 and then fed that back into the calculation 15 times. This little application allows you to iterate up to 1000 times and is lightning fast!
The flowchart highlighting the steps to take is shown below.