The 4 Basic Operators
We deal with these every day of our lives, whether we are adding up shopping bill items, taking our weekly bill away from our allocated budget, working out how much a certain number of items will cost us given the price of one of them or splitting up our wages/salary into equal chunks to last us for the month. Since we were small children, we have done this in one way or another and probably not given very much thought to it (except in maths class when we probably had very little choice :-))
This part of the section is going to go over these 4 functions and explain how to do it.

The diagram below shows the symbolic representations of the 4 functions were going to talk about. Top left is a red plus sign representing addition, directly below it is a blue minus sign representing subtraction, to the right of the plus sign is the green sign representing division (as you can see it represents a fraction if you think about it) and finally below that in purple is the cross which represents multiplication.
Since we work in “tens”, that is we use the decimal system, my explanation of these 4 functions will also be a description of the decimal system. Other bases will be discussed separately.
Simply put, we count in tens, we start at 1 (it is very rare that we say that we have nothing of something so that is why we wouldn’t start at 0 although the number 0 does feature prominently in the decimal system as a placeholder, more on that later) and we proceed through 2, 3, 4…9. When we reach 9 we have to start on “another 10” so we indicate this by representing our “unit account” as being reset to 0 and then our tens (that is our completed batches of 10) are incremented by one, and we start again at 1 through 9 for our next batch of 10.
It might be simpler to think of it like this. Imagine having a tray, not unlike an egg box, with 10 holes, each of which can hold one item. We pick up our first item and place it in any empty hole in the tray.

We now have 9 free holes.
We pick up our next item and place it again in any free hole.
Now we have 8 free holes.
We continue to pick up items and place them into free holes until there are no free holes left, whereupon our tray is full and if we wish to continue collecting items we need another tray (that is we have a completed 10, but if we have more items than 10 we need to start on a second 10 until we have completed counting items.
Assume that we have more than 10 items, so we pick up another blue tray and start filling it up in the same way that we did the last one, but having reached 10 on the second tray we find we still have more items:
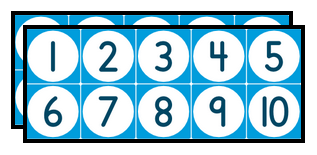
We keep filling up trays until we run out of items to put in them, let us assume that we filled up four trays and we have 3 items left over:
We have 4 completed trays with 10 in each one and 3 left over:
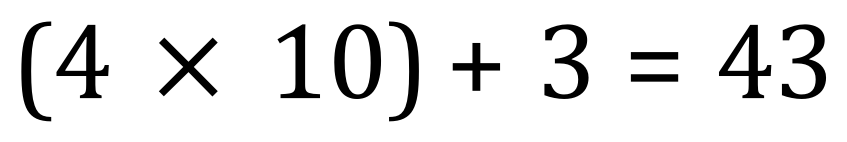
So in fact we have 43 items.
What about if we had actually filled up 10 trays before we found that we had 3 leftover? Well this time of course we would have 10×10 which is 100, plus the remaining 3 which is 103.
What this is in fact leading us to is the fact that we ordinarily count in tens, and when we fill up a 10 we start on another one, until we’ve filled up 10 of them, and we call a group of ten 10s = one “100”.
When we reach 10 groups of 100, we call this 1000, and 10 of these is called 10,000. In our primary school education we are taught “hundreds, tens and units” and this forms the basis of our mathematical learning.
|
Hundreds (100) |
Tens (10) |
Units (1) |
|
|
4 |
3 |
|
1 |
0 |
3 |
Earlier on, we said we had 4 trays full with 3 leftover, the top line of the table above shows as this is a number, i.e. four tens, and 3 units. A little bit later on we suggested that we might have 10 full trays, and 3 left over. Now this time we won’t write 10 in the tens column, because we already said that when we reached ten 10s we call this 100 so we put one in the hundreds column and 3 in the units column. We don’t have any ungrouped trays of 10 lying about so this time we put a 0 in the tens.
With me so far?.....good 8-)