Volumes of Gases
Calculations involving molar quantities of gases can be performed if we consider the volume that a particular amount of gas takes up at a specified temperature and pressure. At any given temperature and pressure molar quantities of gases will occupy the same volume. Therefore if a mole of carbon dioxide occupies a certain volume at a given temperature and pressure, then a mole of oxygen, chlorine, methane, whatever will occupy the same volume at the same temperature and pressure.
At room temperature and pressure (room temperature is given as 20°C, 293 K and a pressure of 1 atm, or 101,325 Pascal) a mole of any gas will occupy 24 dm3 . In some older textbooks the molar volume of the gas is quoted at 0°C, 273 K and 1 atm as 22.4 dm3 but the first definition applies now.
Q. What is the volume of a mole of helium gas at 20°C and 101,325 Pascal?
A. A mole of helium has a mass of 4.003 g and will occupy 24 dm3
Q. State the volume of 3 moles of krypton gas at room temperature and pressure.
A. There is no trick here, volume of 1 mole would be 24 dm3 at room temperature and pressure so 3 moles is simply 3×24 which equals 72 dm3
It can be seen therefore that if you know the relative molecular mass/relative atomic mass of the gas and either the mass of the gas or the volume it occupies, you can work out its volume or mass respectively. Let us now take a look at a couple of examples to clarify this:
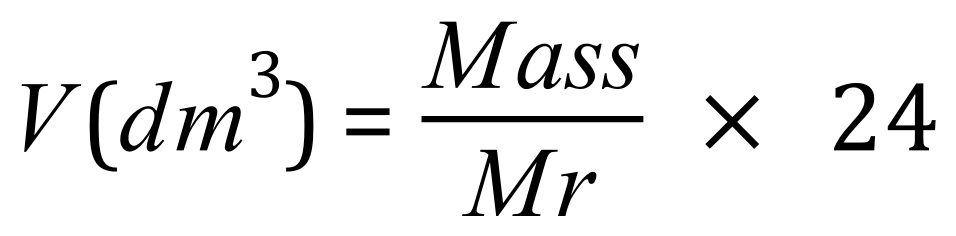
From the equation we can see that 44 g of carbon dioxide would occupy 24 dm3 as the relative molecular mass of carbon dioxide is 44, and 44÷44=1
Q. What would be the mass of neon gas to occupy 12 dm3?
A. Again there are no tricks here, we are given the volume (12) and we need to know the mass of neon that would occupy that volume. This does require that the formula above is rearranged so that the mass of the gas is made the subject of it:
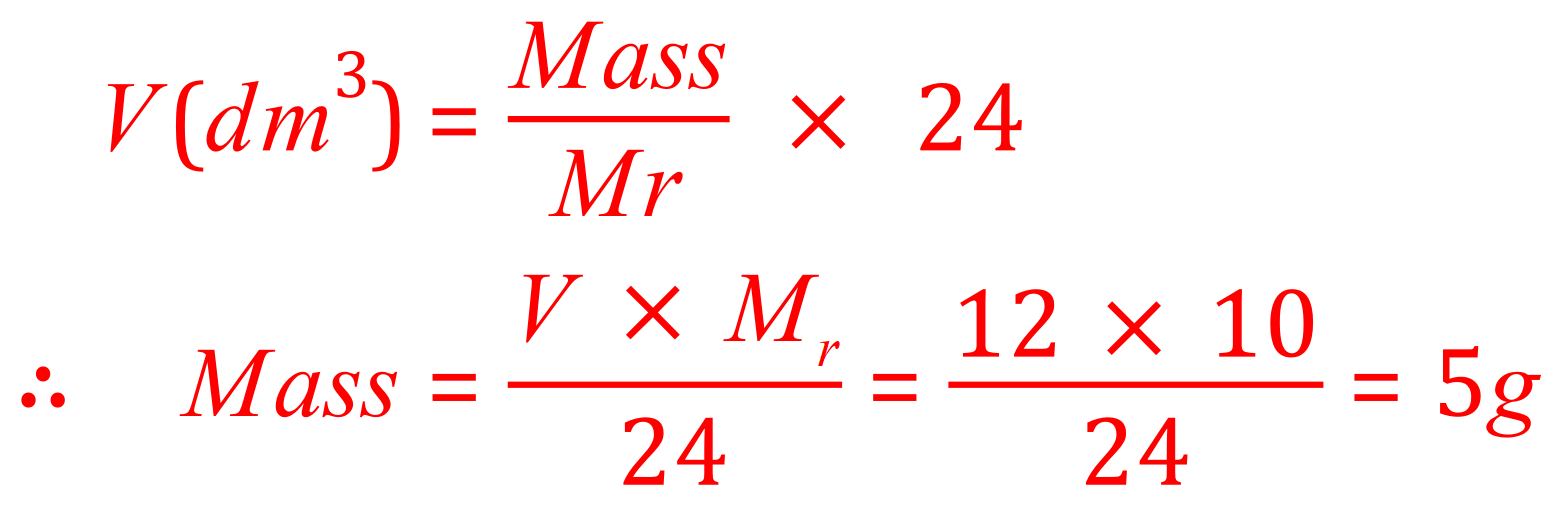
Q. What volume would be occupied by 71 g of chlorine (molecular) at room temperature and pressure?
A. Notice that the question specifies molecular, chlorine is diatomic and therefore one mole of chlorine molecules would have twice the mass of a mole of chlorine atoms. With this in mind we can now proceed to the calculation, given the fact that the relative molecular mass of chlorine gas (atomic) is 35.5.
The relative atomic mass of chlorine (atomic) is 35.5 and in this diatomic state is 71 because it is in fact Cl2
We can use the equation in its standard state, and for this particular example we don't even need to write it out because the volume is 71÷71 times 24 which you should be able to work out as 24. In other words 71 g of diatomic chlorine is a mole and therefore would occupy 24 dm3 at room temperature and pressure.
Q. Butane gas burns completely in air according to the following equation:

(a) what volume of carbon dioxide is produced when one mole of butane is burnt in excess oxygen?
(b) what volume of oxygen would be required to burn 6 moles of butane?
(c) what mass of water will be produced as per the equation given?
A.
(a) we can see from the equation that if we burn 2 moles of butane we will produce 8 moles of carbon dioxide, therefore it is logical to conclude that burning 1 mole of butane will produce 4 moles of carbon dioxide. The question has not stated otherwise, so we assume that we are working at room temperature and pressure, and as we know, one mole of any gas under these conditions will occupy 24 dm3 . Since we are producing 4 moles of carbon dioxide we can see that we will produce 4×24 = 96 dm3 carbon dioxide.
(b) from the equation we can see that we require 13 moles of oxygen (diatomic) to completely burn 2 moles of butane. Therefore to burn 6 moles of butane will clearly require 3 times as much, i.e. 39 moles of diatomic oxygen. One mole of diatomic oxygen will occupy 24 cubic decimetres at RTP so 39 moles will occupy 39×24 = 936 dm3
(c) from the equation we can see that 10 moles of water will be produced, one mole of water has a mass of 18 g therefore this equation here would produce 180 g of water.
Q. During a chemistry investigation, a student burnt exactly 60 g of ethane gas in excess oxygen, producing amounts of carbon dioxide and water as per the balanced chemical reaction given:

The volume of carbon dioxide given off was measured and found to be 96 dm3 . What does this information suggest to you with regard to the conditions under which the gas was burnt?
A. One mole of a gas at RTP occupies 24 dm3 and the student collected 4 times this amount because 24×4 = 96. As 4 moles of the gas occupied this volume it is reasonable to assume that the reaction was conducted at room temperature and pressure.
The carbon dioxide produced in the last question would occupy a greater volume if the temperature had been increased from 20°C or the pressure reduced from 101,325 Pascal. Similarly if the temperature was decreased and/or the pressure was increased the volume occupied by the gas would reduce. We will come to calculations of this nature when we look at the gas laws.
Q. A student burns a quantity of carbon in oxygen, noticing that at the end of the reaction, some carbon is left and 40 dm3 of oxygen gas has been used. Mass of the carbon left is 62 g, what was the starting mass of carbon?
A. This could be quite a tricky question, the inference is that the limiting reactant in this case is oxygen as there is carbon left so it must clearly be in excess. We are told that there is 62 g of carbon left so clearly what the question is asking is for us to establish how much carbon was used. For this, as is always the case we need to balance chemical reaction between carbon and oxygen:

The balanced equation for this is quite simple, we can see that one mole of carbon will burn in one mole of oxygen gas (diatomic) to produce one mole of carbon dioxide gas. We are told that the student has used 40 dm3 of oxygen gas. We know that one mole of a gas at RTP occupies 24 dm3 so we can quickly establish that we have used 40÷24= 1.67 moles of oxygen gas. As the equation tells us that the reaction is one-to-one we can establish that we must also have used 1.67 moles of carbon.
1.67 moles of carbon has a mass of 1.67×12 = 20 g and the student noticed that there were 62 g left, starting mass must therefore have been 82 g.
Q. Nitrogen dioxide decomposes when heated according to the following reaction:

What is the total volume of gas produced when 25 dm3 of nitrogen dioxide gas is decomposed this way?
A. First of all we should consider the equation we have been given. 2 moles of nitrogen dioxide gas decomposes to produce 2 moles of nitric oxide gas and one mole of oxygen gas. The question asks us for a total volume, therefore we need to know a little bit about the volumes of molar quantities of gases. One mole of nitrogen dioxide would occupy 24 dm3 at RTP but the question tells us we actually start with 25, so the number of moles of nitrogen dioxide must be 25÷24= 1.042 moles. The equation tells us that 2 moles of nitrogen dioxide decomposes to form 2 moles of nitric oxide and one mole of oxygen. Therefore one mole of nitrogen dioxide would decompose to produce one mole of nitric oxide and half a mole of oxygen. Taking this one step further we can therefore say that 1.042 moles of nitrogen dioxide would decompose to form 1.042 moles of nitric oxide and 0.521 moles of oxygen. Dealing in molar quantities we have a total molar volume on the right side of the equation of 1.042+0.521=1.563 moles. One mole of any gas at RTP occupies 24 dm3 therefore 1.563 moles will occupy 1.563×24= 37.512 dm3.
This calculation could have been made simpler by taking into account the fact that 25 dm3 on the left-hand side represents the 2 moles of gas decomposed (taking into account molar quantities) and 3 moles of gas will be produced on the right-hand side. So the total volume of gas is 25+ (25/2) = 37.5. Far simpler of course but getting used to the mathematics is quite a good thing to do.