2 Dimensional Shapes
Anything referred to as being “Two Dimensional” or simply “2D” exists in only two dimensions, possession only length and width, not height.
Pause for a moment (yes of course we have only read 2 lines so far but, do it anyway) and try to think of some objects that you may have come in contact with that are two-dimensional, you will probably find that it is not as easy as it may seem. A photograph of a person is in fact a three-dimensional object because it possesses a width, a length and a height (but we would call it thickness in this case, because we would be considering the thickness of the paper it was printed on) but of course it is the subject of the photograph that is represented as a two-dimensional object!
Why is a photograph three-dimensional you are asking me now? Well think about it, a 6” x 4” photograph (for those of you born into the metric system that’s 150 mm x 100 mm) also has a thickness, albeit this may only be about a 10th of a millimetre but nonetheless it is still there, this therefore makes your seemingly two-dimensional object a three-dimensional object and therefore you could (if you wanted to) measure its volume.
For the purposes of this particular section we are going to disregard the fact that the object is technically three-dimensional and concentrate on the obvious 2 dimensions of length and width. Therefore we can define a two-dimensional object in this way:
“A two-dimensional object or shape is any object or shape that can lie flat on a piece of paper,
or in mathematical parlance a two-dimensional “plane””
Guess The Film? *
A “plane” in turn can be thought of as a piece of paper which extends length wise and width wise infinitely.
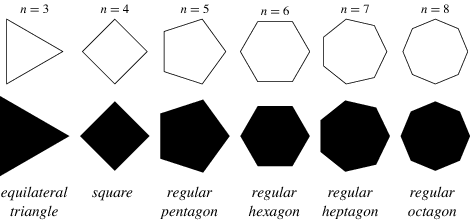
When we look at two-dimensional objects in mathematics we are usually considering things like triangles, squares, pentagons and so on and we are interested in the mathematics of finding out such things as the perimeter (that is the distance all the way around the edge of the object) and the area it encompasses. Additionally, we might also want to look at the symmetry of the shape and to work out how many lines or orders of symmetry it might possess (reflective, or rotational symmetry and this will probably become a chapter or at least a section on its own because it can become quite involved topic in its own right).
What is the simplest two-dimensional shape you can think of?
You might be thinking that a simple straight line is the simplest two-dimensional shape, but in fact it’s not. The line has only one dimension, which is its length. The line has no width and it has no height. The “dimensionality” (of course no such word exists, but it sometimes helps to make them up!) of an object is defined mathematically as the minimum number of coordinates needed to specify the location of a point contained within it.
Let me try to explain that a little bit better:
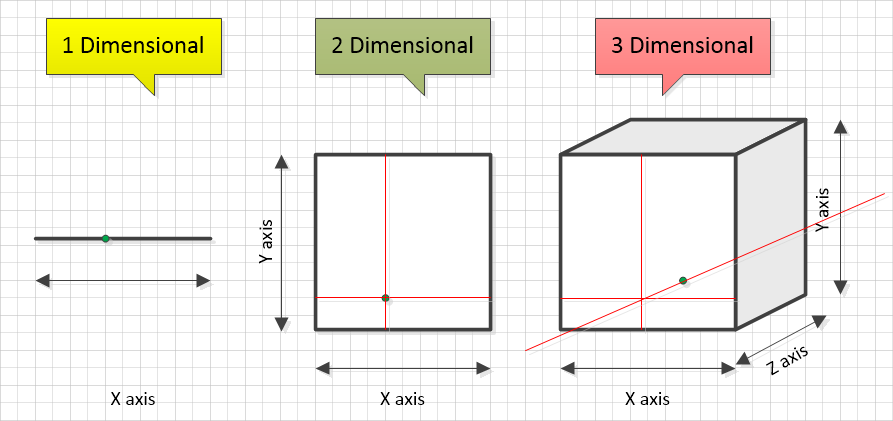
Now we are going to enter very briefly the world of coordinate geometry.
If we take a look at the one-dimensional object, the straight line, you will notice that it has indeed only one-dimension. The Green point on the line is at position +4 on this line (assuming that the origin of the line is the extreme left end, and that we have elected to call this “0”). If we liken this to the “number line” we can head off to the right infinitely using positive values and head off to the left infinitely using negative values, but for our purposes we will stick to plain old 4. Conventionally coordinates in 2, and 3 dimensional space, are written with the X coordinate first, followed by the Y coordinate and then Z coordinate if applicable.
So for example our Green point on the one-dimensional line would be at position (4). If we move to the right, to the two-dimensional line we will see that our point remains at X equals 4 but now it has a second coordinate in two-dimensional space which is Y equals 2. This time the coordinates of the points will be written (4, 2) denoting, by convention, the X coordinate first followed by the Y coordinate.
Consider our three-dimensional space, our Green point is, once again at X equals 4, Y equals 2 but this time it is displaced along the Z axis by 3 points (this isn’t particularly easy to visualise on a two-dimensional page, but please try to bear with me). The coordinates of this point in three-dimensional space would then be written (4, 2, 3) denoting the X, Y and Z coordinate values.
Since this particular chapter is only going to be interested in two-dimensional space, we can jump out of the world of coordinate geometry for the time being anyway.
*Snakes On A Plane