Angles On A Line
Before we dive headlong into the world of geometry and two-dimensional shapes, there are a few basic angle properties that we need to understand. Mastering these basic rules will make the vast majority of your experiences with geometry a little simpler.
The first rule is that the angles at a point on a straight line add up to 180°
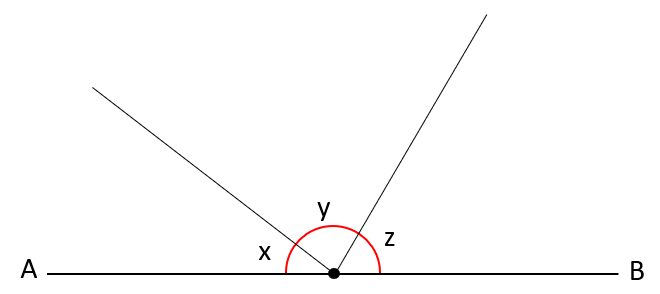
Imagine that the line AB represents a book lying flat on a table. Now imagine the line coming from the midpoint to the left of your page is a single page of that book being turned from its position at A to its position at B. The path traced by the tip of the page from point A to point B completes a 180° turn. At any point along the way the page could be held so that it makes an angle 'x', and subsequently an angle 'z'. Only when the page rests at point B will it have completed a half circle of 180°.
Irrespective of how many pages we are turning, and how many intermediate angles we are producing (I have shown 3 in the above diagram, 'x', 'y' and 'z') the total number of degrees between A and B remains the same, 180°. Therefore all angles at a point on a straight line add up to 180° as stated above. It is quite usual in geometry questions to be given a number of angles, except perhaps the last one and be asked to establish the value in degrees of the missing angle. This is quite straightforward as the sum of the angles that we know subtracted from 180°.
For example if we were told that 'x' was 45° and 'z' was 60° we could establish the value of 'y' as 180 - (45 + 60) = 75°
The second rule is that angles around a point add up to 360°. You should be able to see that this is simply an extension of the first rule where we have carried on past 180° and completed the full circle of 360°.
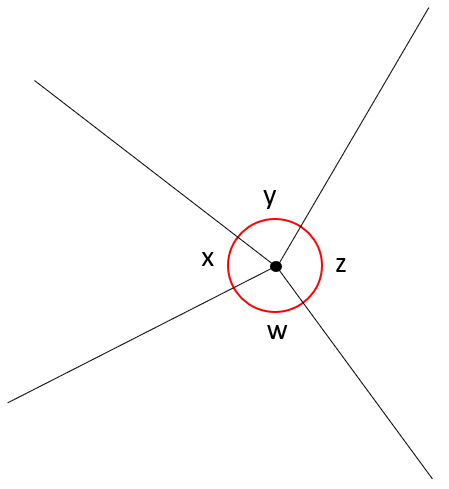
As the second rule is a continuation/extension of the first rule, there is not much more to add. The rule states that all of the angles around a point add up to 360° so you should be able to understand that the values of the angles 'w' 'x' 'y' and 'z' , make a total of 360° as this is a full circle.
The third rule states that perpendicular lines meet at an angle of 90° to form a "right angle". A right angle is shown by the placement of a small square where the lines meet. Whenever you see this symbol, the angle being referred to is 90°
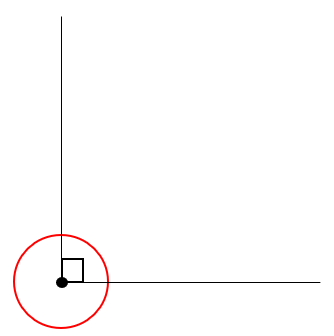
In questions involving angles, you will almost certainly find that the diagrams you are provided with will not be drawn to scale, the temptation might be to get out the protractor to establish the value of the angle you are being asked to calculate. Rest assured this approach will very rarely work!
>> Questions <<