[A] Complex Numbers
The roots of most mathematical inventions and theories are steeped in history and span across many civilisations. The Mesopotamian, Egyptian, Greek, Chinese people as well as the Italians and the French and indeed the English (with the advent of Sir Isaac Newton and his mathematical genius).
It must be said though, that the early interest in mathematics was with the rational numbers, the “normal” numbers that we are all accustomed to, such as 5, 100 and the standard fractions such as three quarters, two thirds and so on. It very quickly became apparent that numbers such as pi, and the square root of 2, were “irrational”, that is they had not got a fixed, finite value and in the early days of mathematics this did cause some concern, so much so that the Greeks initially refused to accept “root 2” as a number indeed!
Another bone of contention, in the Renaissance period of the 15th and 16th centuries were negative numbers, numbers which we take for granted nowadays but to the mathematicians of the time they were unusual and treated with caution.
If we consider very simple algebra, such as for example the following equations:
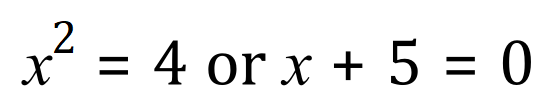
we can see that these are indeed very simple to solve, gives us a value for 'x' equals +2 or -2, and in the second example 'x' equals -5, but what about this equation?
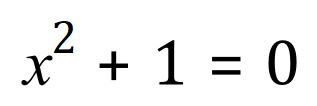
If we permute as if we were going to try to find a value for X, we will see that X squared equals -1 and therefore X squared should theoretically be the square root of -1, but we know that we can’t have square roots of negative numbers, so what’s going on? Mathematicians are funny creatures, and if you tell a mathematician that something can’t be done, or that he can’t have something, he will almost certainly find a way of creating it.
Such is the case with the square root of -1 which mathematicians decided to accept as existing, and they called it ‘i’.
The mathematician Cardano post himself a little problem by trying to evaluate the dimensions of a rectangle whose perimeter was 20 units, but whose area was 40 square units. In fact such a rectangle does not exist in reality and although Cardano technically “solved” his problem using algebra which ultimately involved the use of square roots of negative numbers he decided to accept it anyway. In the 17th century the mathematician Descartes decided to regard these numbers as “creatures of the imagination” and hence they became known as “imaginary numbers”.
Let us take a look at an example of Cardano’s rectangle problem, that can be solved .
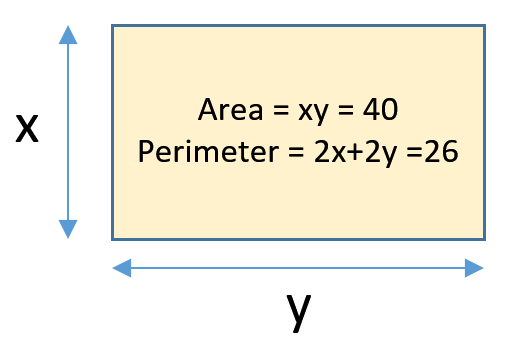
We can quickly work out the respective values of X and Y being 5 and 8 but let’s see how, algebraically, we could do this:
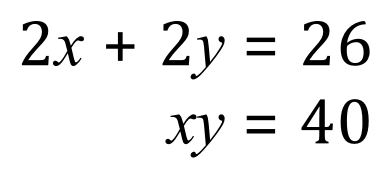
Just for the sake of simplicity we will divide the first equation by 2 throughout:

Now we have 2 variables which could complicate matters, so what we do next is we will manipulate y in terms of x:
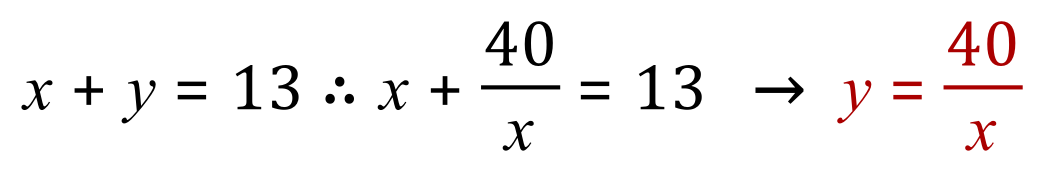
If you’re not sure where the 40 divided by 'x' expression came from, consider the second equation which shows the product of 'x' and 'y' and you should be able to see it.
Multiplying throughout by ‘x’ to remove the fractional expression, and if we then rearrange we will come to the quadratic equation:

Using the formula for the roots of a quadratic equation, with values for ’a’ =1, ‘b’ = -13 and ‘c’ = 40 we will arrive at values of 'x' = 5, and 'x' = 8 which, you can see, satisfy the requirements for the perimeter/area/dimensions of our rectangle. So in fact this type of rectangle does exist, so why didn’t the previous one exist?
Well, physically it doesn’t but mathematically does using the square roots of negative numbers and complex algebra.
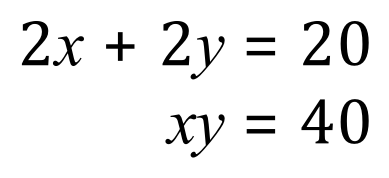
Just as in the previous example, divide the first equation throughout by 2:
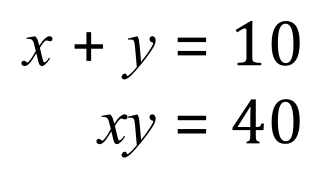
Again, we will re-express ’y’ in terms of ‘x’:
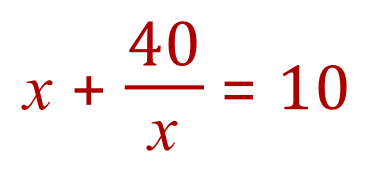
This will lead to the following quadratic equation:
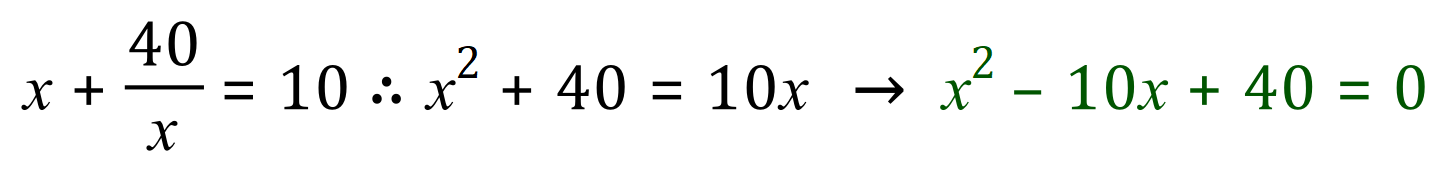
The roots are complex in this case and although the actual rectangle can’t exist in the real world we can produce solutions to the equation if we consider complex numbers. Let us take a look at the formula for the quadratic equation, and insert our coefficient / constant values:
‘a’ = 1, ‘b’ = -10 and ‘c’ = 40
Plugging these values into the formula we arrive at this:
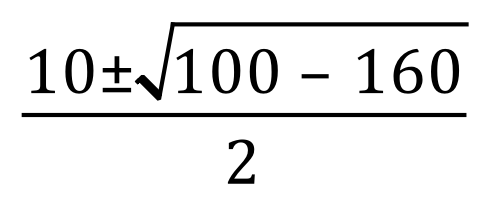
Straight away, you should be able to see that the determinant is negative, because we end up with the “square root of -60”. Mathematicians refuse to be defeated, and bring into play one of the rules with regard to the permutation of surds:

So, taking this into account let us re-express our value for the determinant above this way:
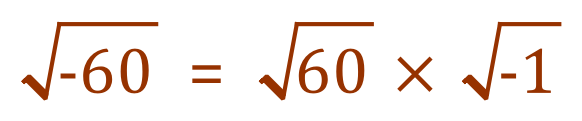
Wait, hang on a minute, didn’t we say that the square root of minus one was called ‘i’ ?, In which case, can’t we say this?:
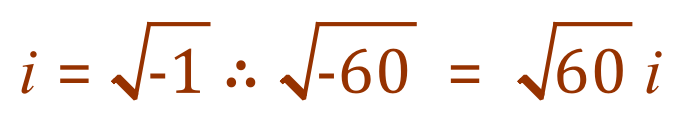
Well, we can and we do......also, we can simplify the square root of 60 using prime factorisation:
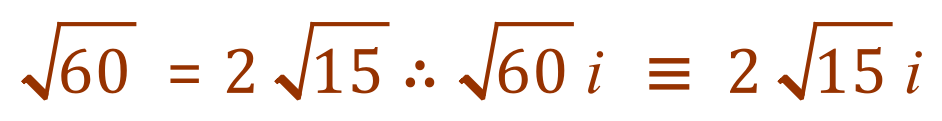
Don’t forget though, that all we’ve been doing so far is simplifying the determinant of the quadratic equation, we now need to do the rest of it.
Based on what we have so far:
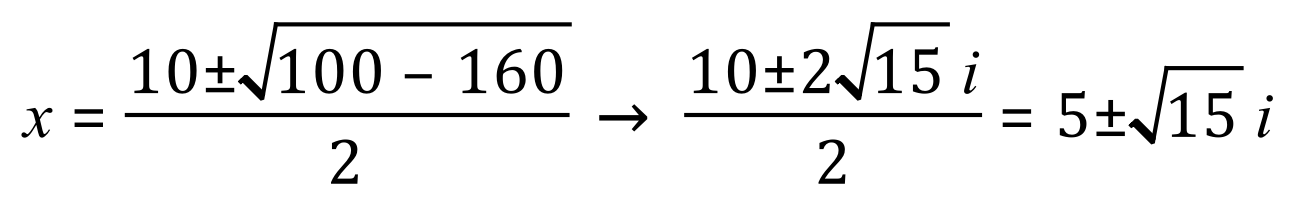
So although Cardano’s rectangle can’t physically exist, we now have values for the dimensions that would make it work in a mathematical context. let us now "reverse engineer" our findings to see if we can get back to where we began:
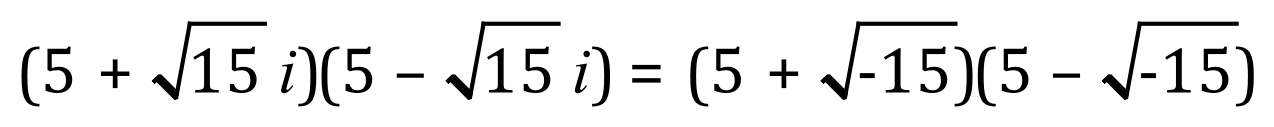
Expanding:
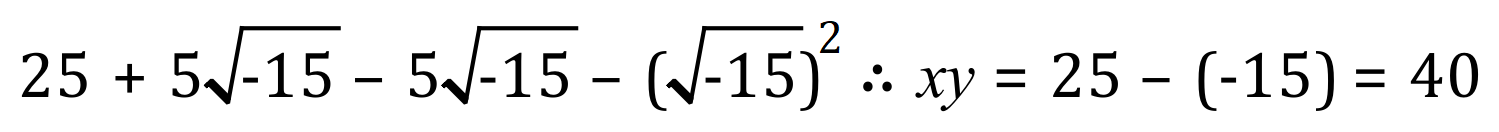
Let’s not forget the perimeter:
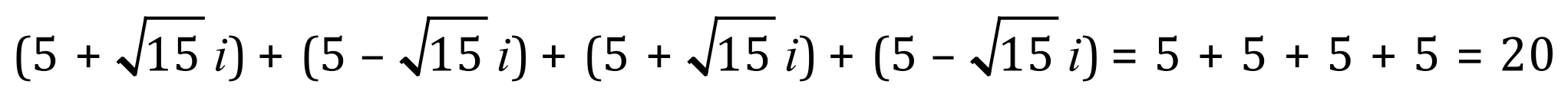
If you cast your mind back to the beginning, you will see that a perimeter of 20 and an area of 40 was the original problem.
Okay, so now we have this wonderful new invention called “i” which we are seeing can behave like a proper number if we wanted to, but what else can we do with it?
Well pretty much anything you can do to a rational number, you can do to complex number. We will now take a look at some of the basic operations that can be performed on complex numbers.