When you look at subtraction of normal arithmetic integers, for example 4-3 we usually just accept that the answer is 1. We subtract 4 from 3. What bill also doing, but we don't take a lot of notice of is performing an addition of a negative number. Subtraction is in fact negative addition but I don't want to complicate matters too much.


If we take matrix B away from matrix A we would write it like this:


A - B


But we could also write it like this:


A + ( - B )


This may seem a little bit pointless but it leads onto an important factor with regards to matrix subtraction. As is the case in matrix addition, only matrices of the same size can be subtracted purely because of this rule that shows that matrix subtraction is in fact the addition of a second matrix which has been multiplied by -1 (scalar).


Example:






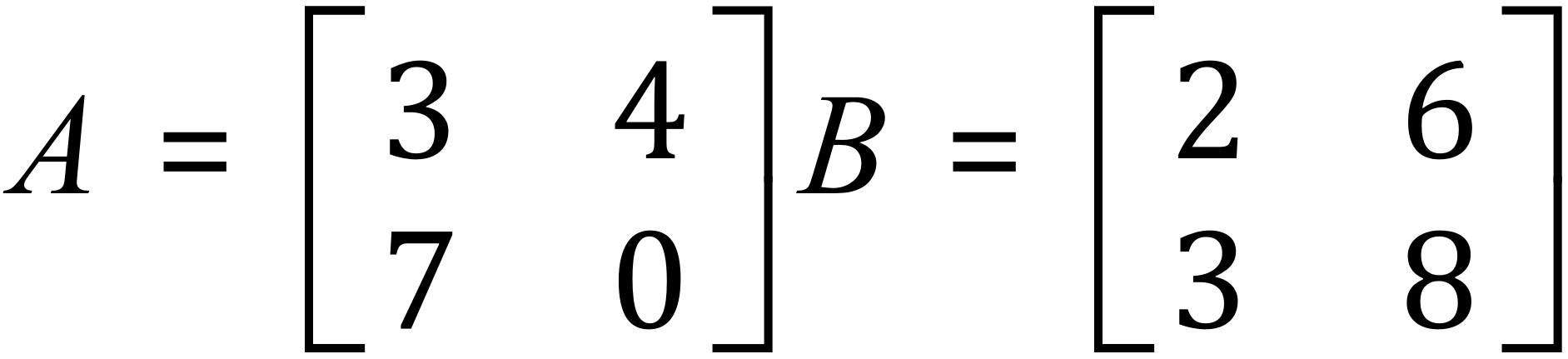
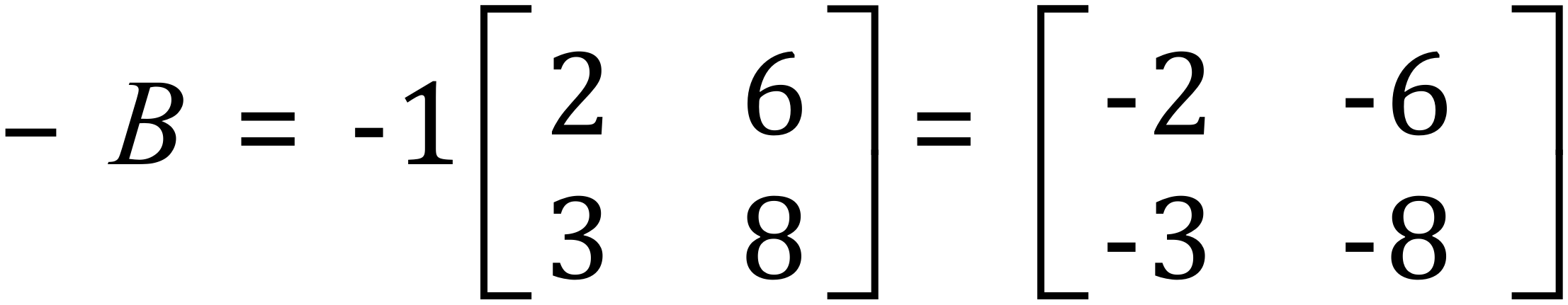
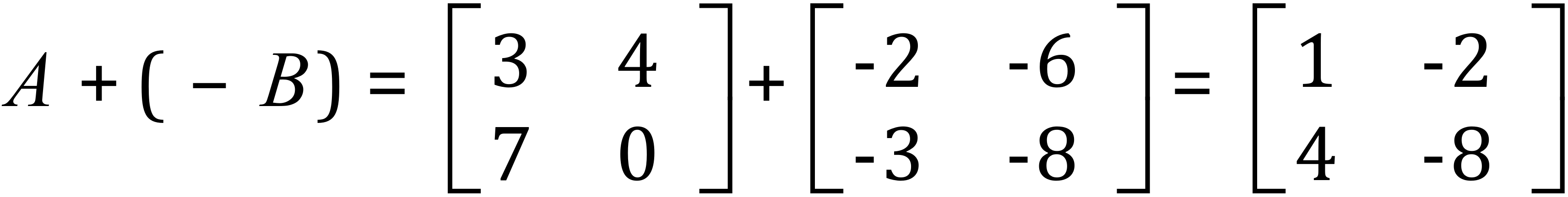
Essentially, matrix subtraction is performed in the same way as matrix addition by operating on corresponding pairs of elements.