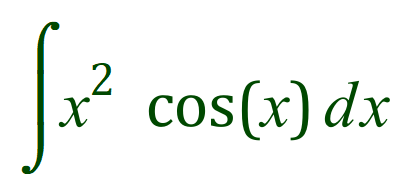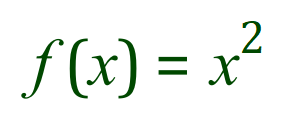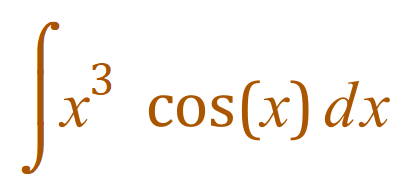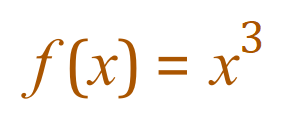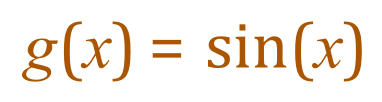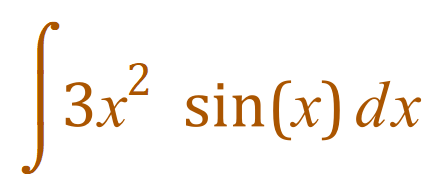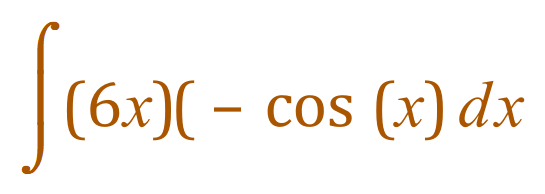[A] Integration By Parts
Things start to become a little trickier when we start looking at multiply functions together, we need to apply a new set of rules which are a little more complex than those we have seen already.
The formula for “Integration by Parts” (IBP) is given as:
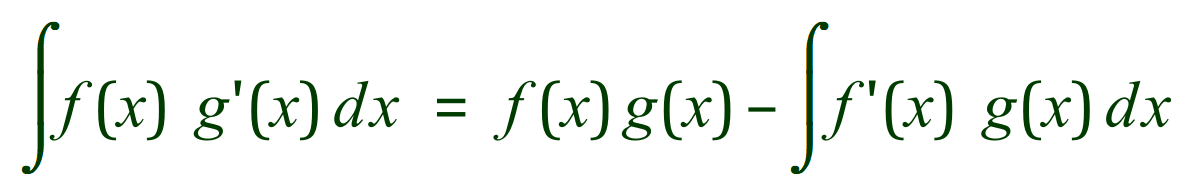
What this formula tells us is that we start off with the product of two functions of ‘x’, we need to evaluate the derivatives / integrals of identified functions and then plug the results into the expression for IBP.
Let’s look at an example:
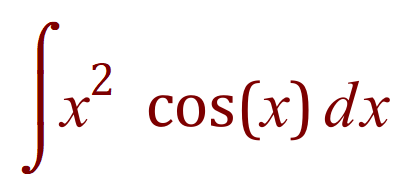
In this case we can see that f(x) is x2 and g’(x) is cos(x).
So:
- If f(x) = x2 then f’(x) = 2x
- If g’(x) = cos(x) then g(x) = sin(x).
We now have FOUR expressions to plug into the equation for IBP:
|
|
|||
|
|
|||
|
|
|
|
|
Using the equation for IBP as shown:
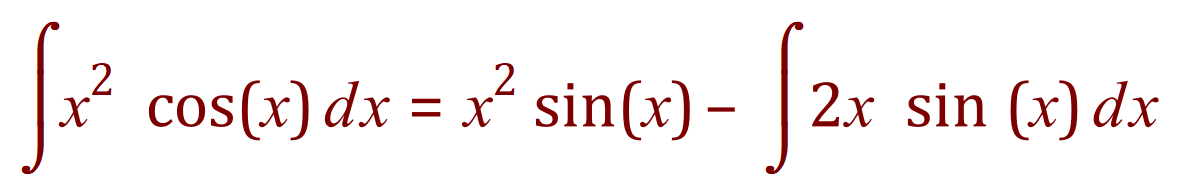
Hmm….we are no further forward, or so it would seem, as we now have another IBP problem…the last part of the expression, however the resolution of this part is usually simpler because the second IBP is often easier:
Take the “Sub Integral” and tabulate as above:
|
||||||||||||
Now work the IBP equation to obtain a result:
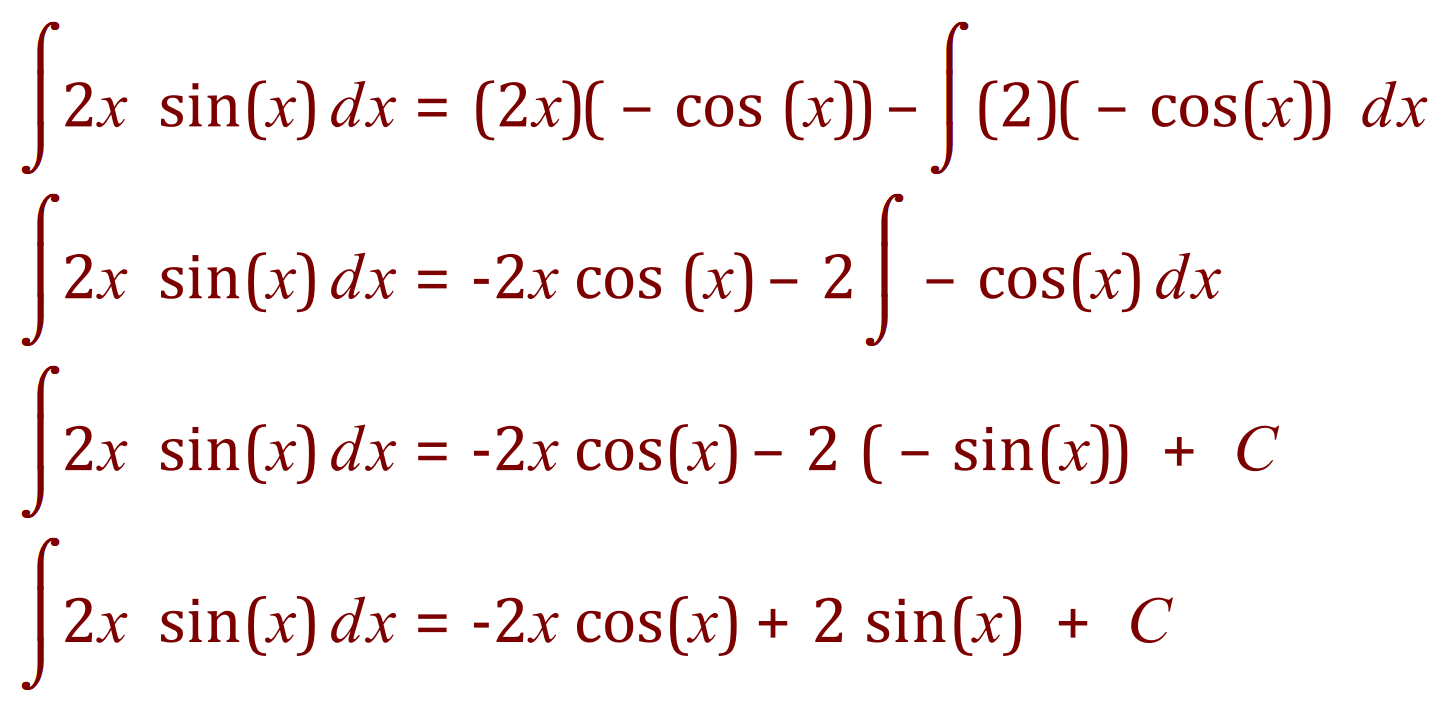
Remember though, that this is the answer to the sub integral only, we have to now substitute this result back into the main equation to solve the whole problem:
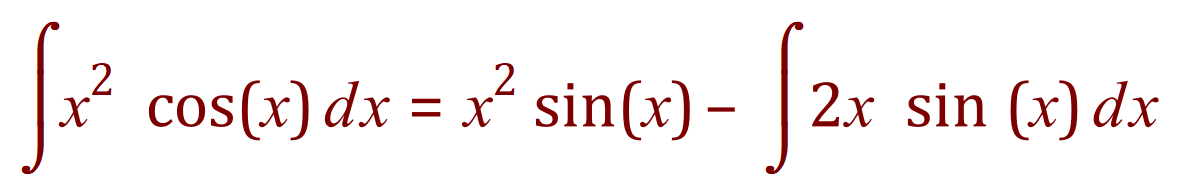
Therefore:
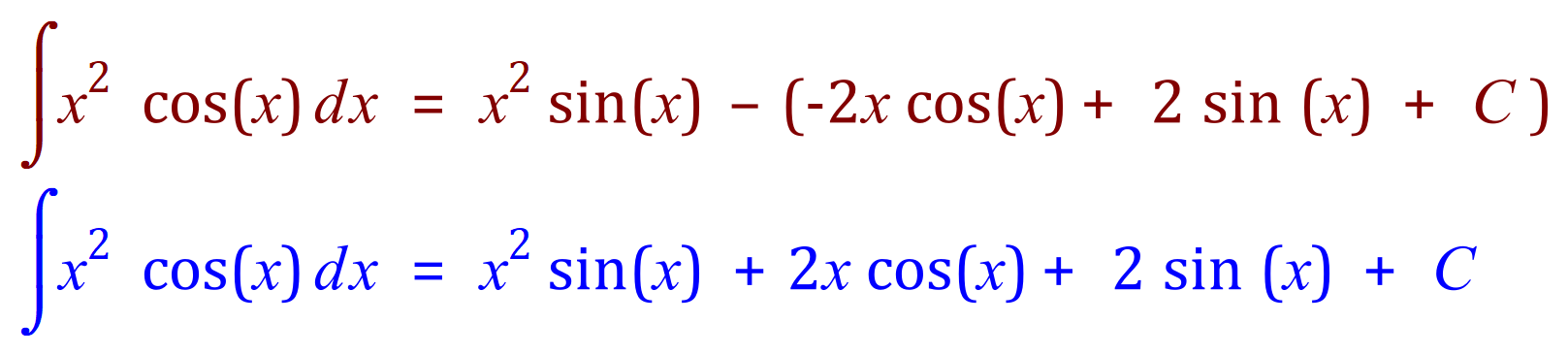
And this is our final answer.
Now we will look at a final example, but this time apart from solving it in the usual way, I will demonstrate a shortcut method which I saw once in a film (biopic) - TIC TAC TOE.
Example:

|
|
|||
|
|
|||
|
|
|
|
|
Therefore:
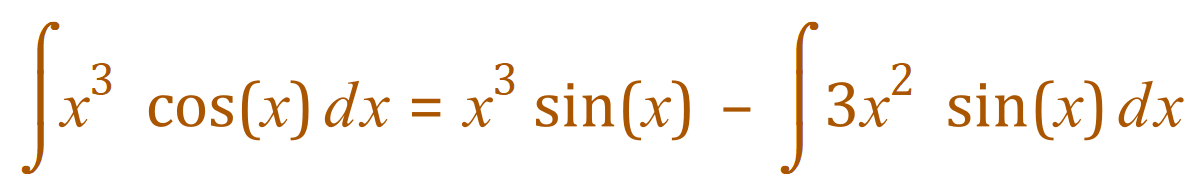
Straight away we can see that we are going into ‘sub integral’ territory, so let’s draw up a table:
|
|
|||
|
|
|||
|
|
|
|
|
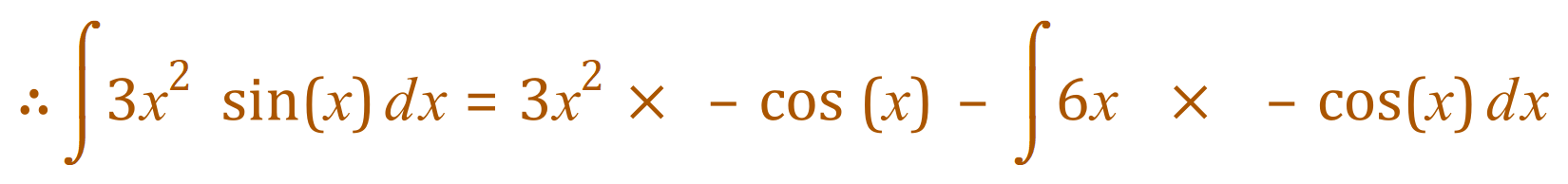
But if you look at the last expression, you can see that we are still “not out of the woods” because we have yet another “sub integral” to deal with however this time having the expression 6x tells me that this sub integral will be the last one.
Once again, let’s create our table for this:
|
|
|||
|
|
|||
|
|
|
|
|
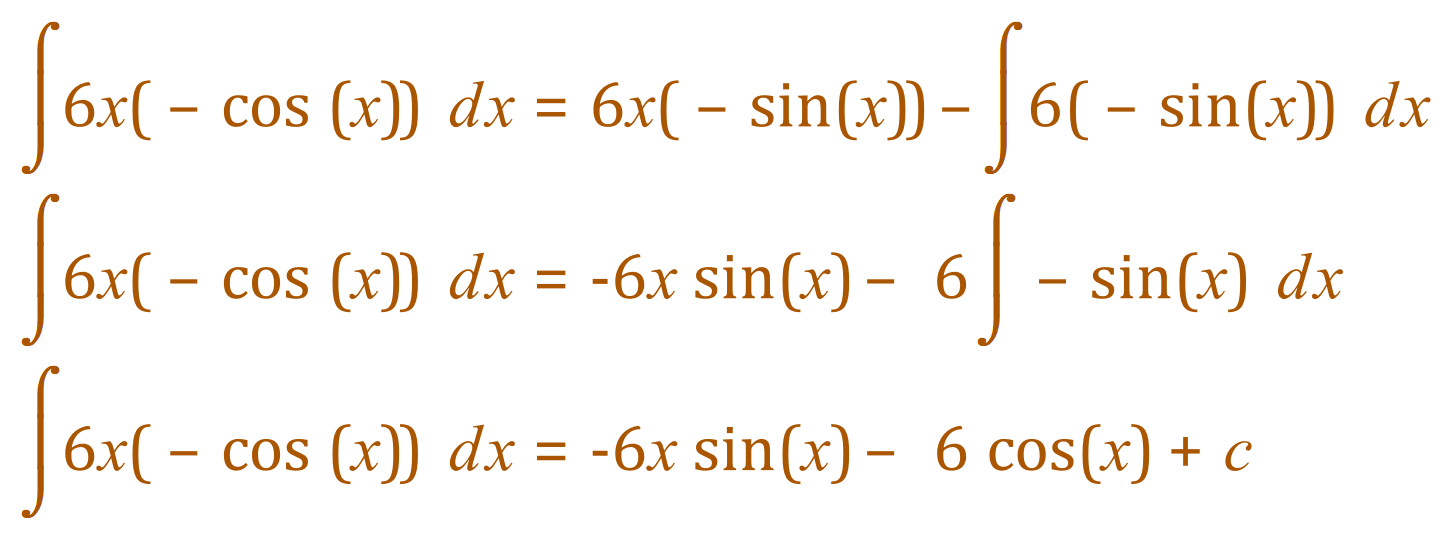
You can now see that we’ve come to the end of the calculations, it is time to start putting this all together to find our answer.
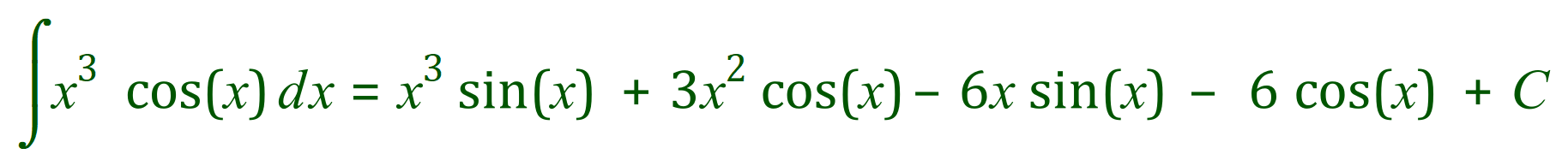
These examples can become more and more complicated, as the powers of ‘x’ increase calculations become more nightmarish.
There is in fact a simpler way to do this on paper so before we reach for the calculator or the computer software (which is quicker but takes all the fun away) let us take a look at a method which I first saw in the film that I mentioned previously, "TIC TAC TOE" from “Stand and Deliver”.
>> Questions <<
Go To >> Table Of Standard Derivatives And Integrals <<