So far we have looked at the algebraic functions of integral calculus, and in particular the constant multiple rule, sum/difference rule and the power rule all of which enable us to reverse the differentiation and produce the “anti-derivative”.


Now we are going to look at the trigonometric functions, sine cosine and tangent and look at the indefinite integrals of those functions.


The indefinite integrals of the trigonometric functions can be derived but the derivation/proof is way beyond the intention of this document so we will satisfy ourselves with being given the values of the integral functions and just take them as ‘accepted’ without formal proof.


In the document on differentiation I produced a list of standard derivatives, I will now produce a list of some of the more basic standard integrals for you to study and become familiar with.






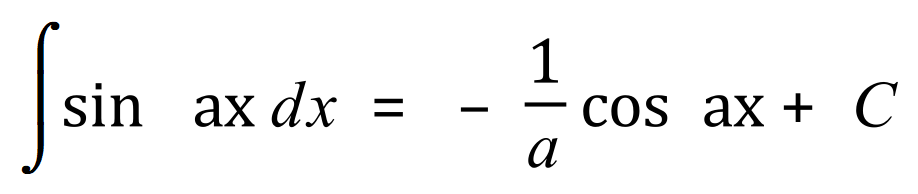
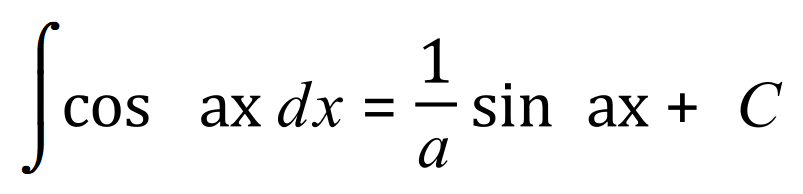
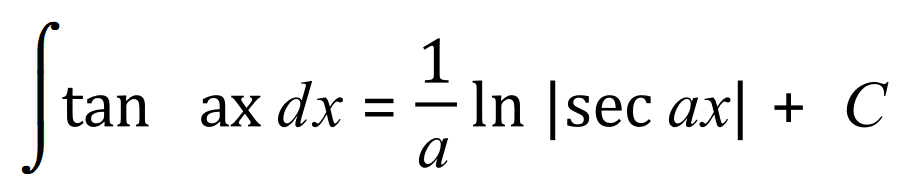
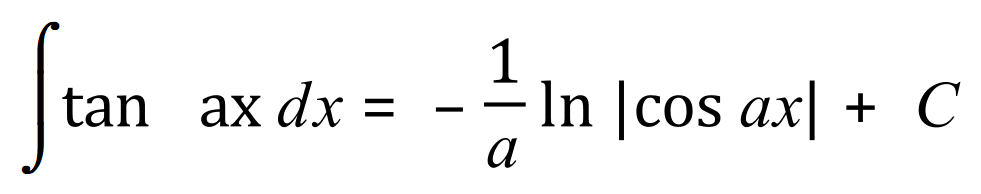
Remember that the constant is just as important with the trigonometric functions as it would be with the algebraic functions because when we integrate we have to take into account the fact that upon differentiation any constant value would vanish.


Let us now take a look at a simple example:


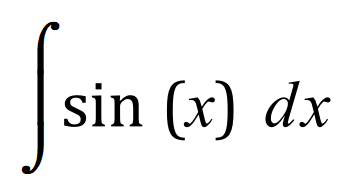
This is a very basic integration and you can probably see already from the table above that the answer is in fact:


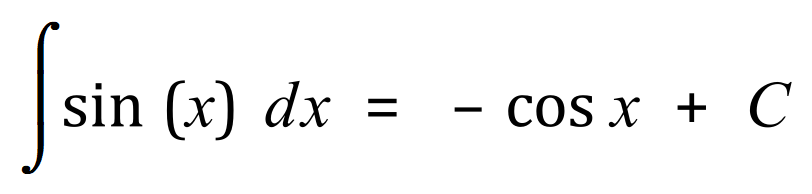
I would probably advise you to consider using the equation above completely, that is even when there is no obvious value for ‘a’ to consider it as having the value of one (that is unity) and to then complete the calculation. With this in mind, let’s take a look at another example:


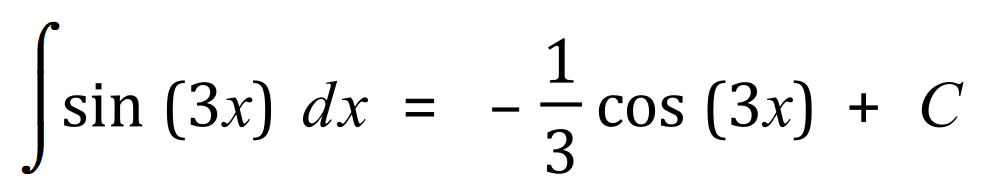
In this case a = 3 so we simply refer to the examples given above, and when we do this we arrive at the answer given.


Things start to become a little bit more complicated when we multiply or divide trigonometric functions either by themselves or by algebraic expressions. When we start to encounter this level of difficulty we have to bring in some extra “tools” such as Integration by Parts and Integration by Substitution.



Go To >> Table Of Standard Derivatives And Integrals <<