[A] Integration By Parts
Remember, that when you are attempting Integration by Parts questions that the formula given below is the base formula to use. Your first attempt at applying the formula may leave you with an integral on the right-hand side as shown, but your first part (the part immediately to the right of the equality sign) will usually be the first part of your answer. Integration by Parts appears to be a process by which the formula is reapplied cyclically until the integrals disappear.
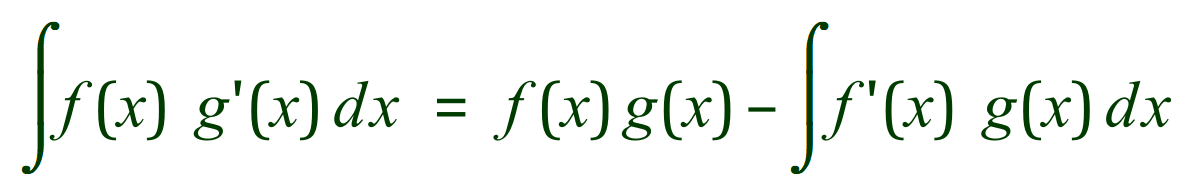
Q1. Integrate, using the integration by parts method, the following expression:
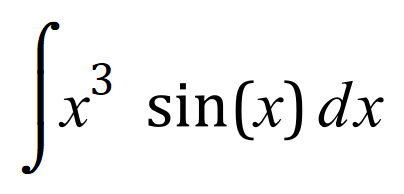
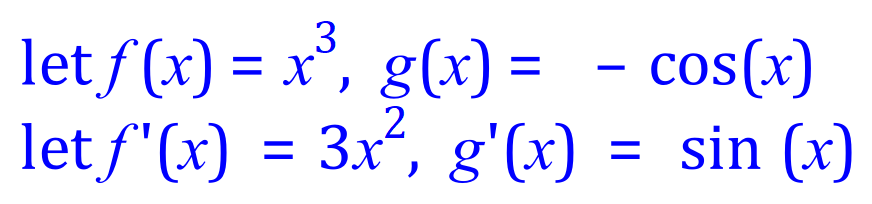
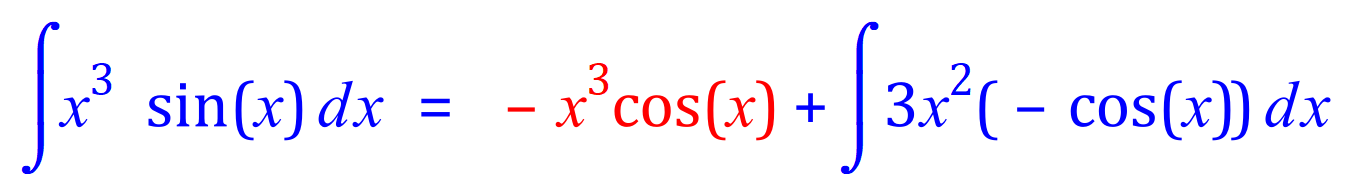
The section highlighted in red is now complete, and we move on to the rightmost integral and treat it as a brand-new IBP problem, allocating values for f(x), f'(x), g(x) and g'(x) as before.
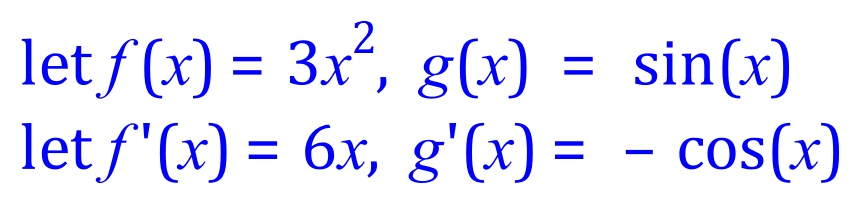
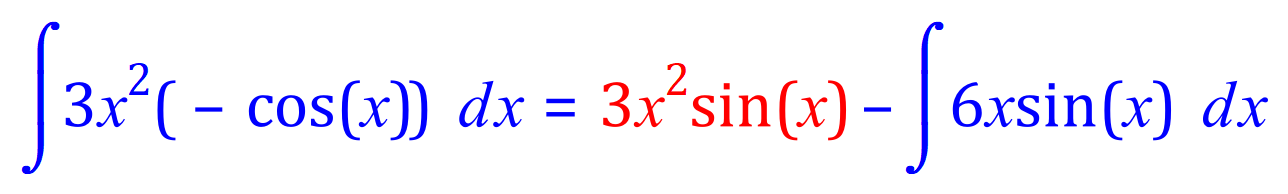
Once more, the red section is complete, however we have an integral to deal with, so we refer back to IBP:
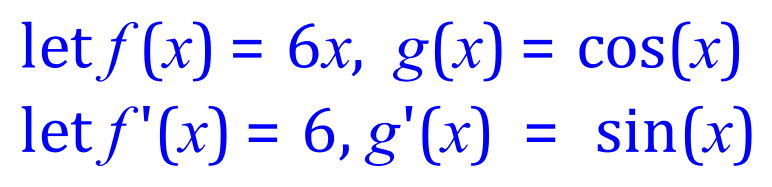
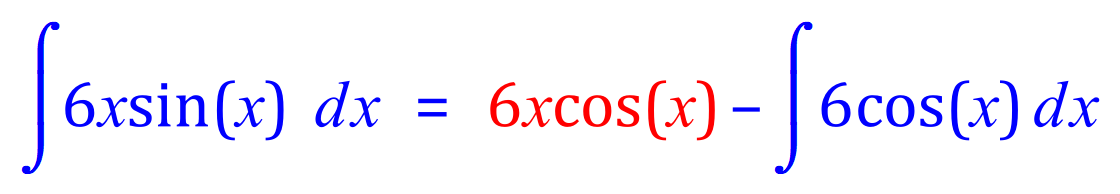
As in previous cases, the red section is complete but this time the integral does not require the use of IBP. This integral is a simple application of the constant multiple rule and is rewritten as 6 times the integral of cos (x):
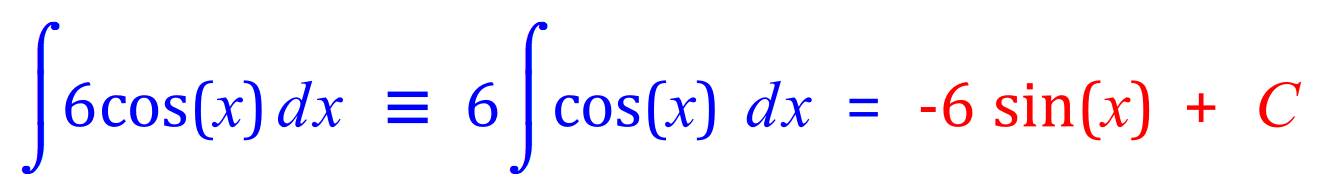
We now collect together all of the red sections to arrive at the overall result for the initial Integration by Parts problem:
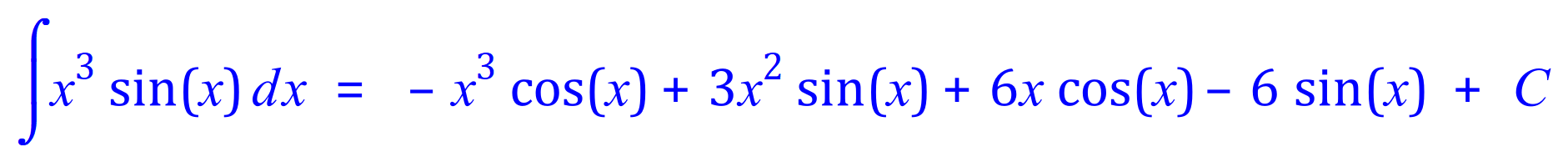
Q2. Integrate, using the integration by parts method, the following expression:
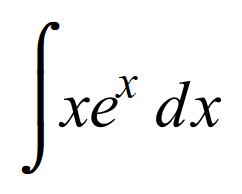
Although this expression looks quite foreboding, just apply the rules as you would in any other case:
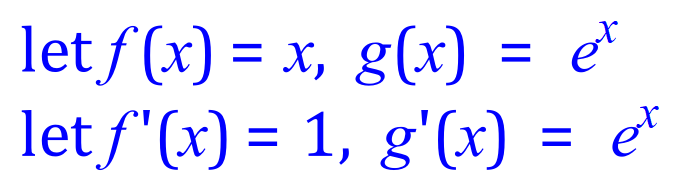

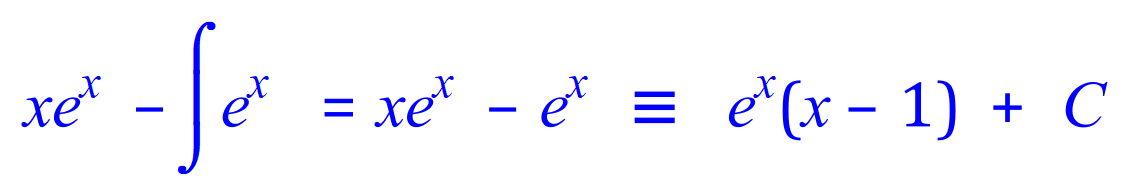
Q3. Integrate, using the integration by parts method, the following expression:
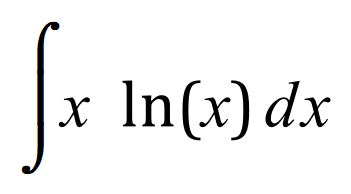
Sometimes it is useful to take advantage of the fact that multiplication is commutative, in other words to entities multiplied together produce a same answer whether we use 'a' x 'b' or 'b' x 'a'. This expression is an example of this, and we make the changes when we allocate our values of f(x), f'(x), g(x) and g'(x):
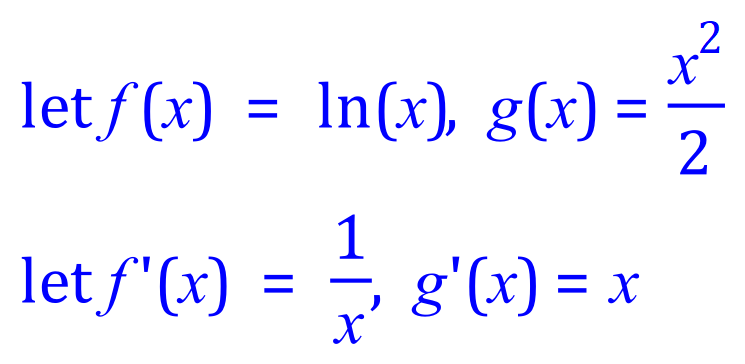
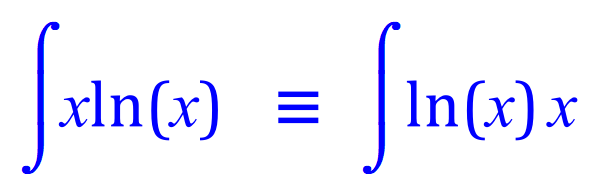
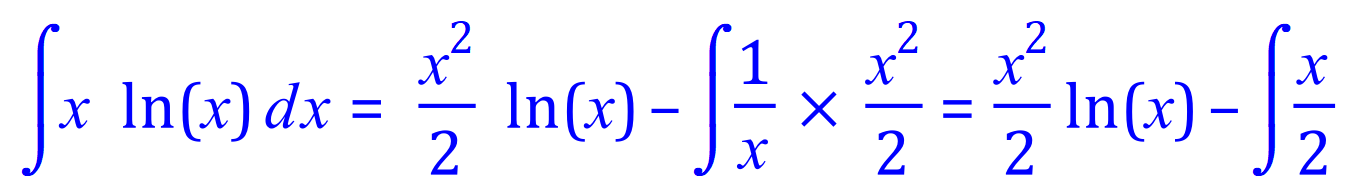
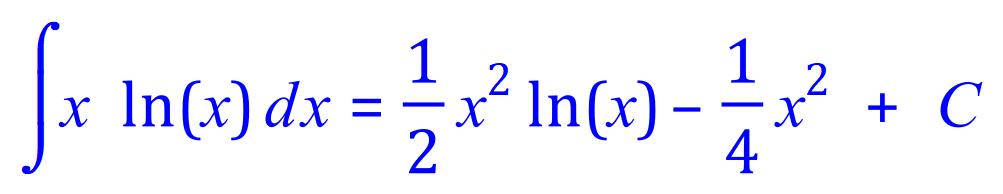
Q4. Integrate, using the integration by parts method, the following expression:

This seemingly horrible integral can be simplified before we even attempt to start working on it. We can split up the "fraction" into 2 separate parts and multiply them together, this way we have a more obvious candidate for Integration by Parts:
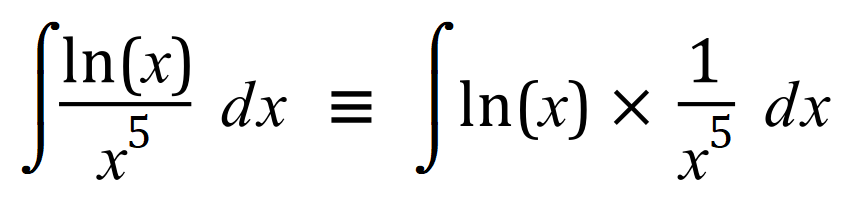
Now the expression looks a little bit friendlier (but not much !), and we can start looking at allocating our values for f(x) f'(x) g(x) and g'(x) as we have done previously.
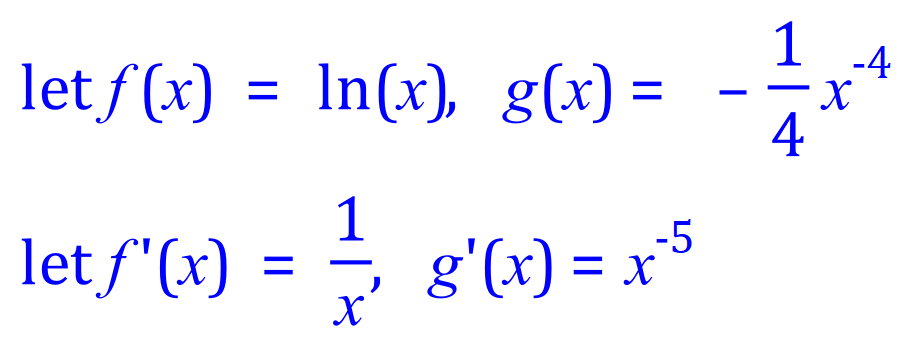
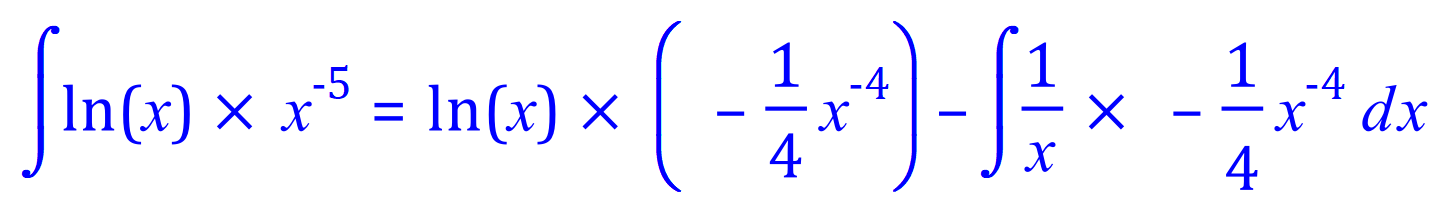


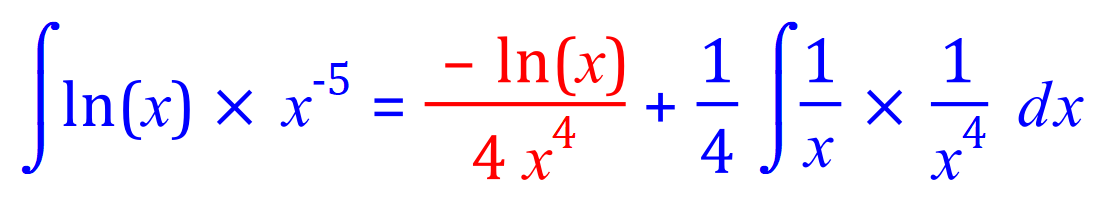

The blue integral on the right hand side is a simple "Constant Multiple Rule" expression:
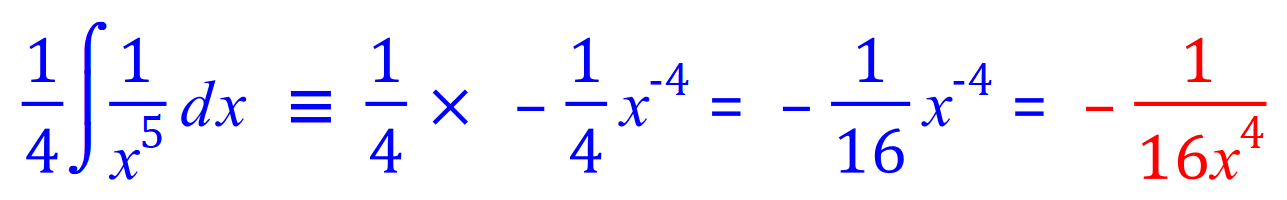
The final expression is therefore:

Q5. Integrate, using the integration by parts method, the following expression:

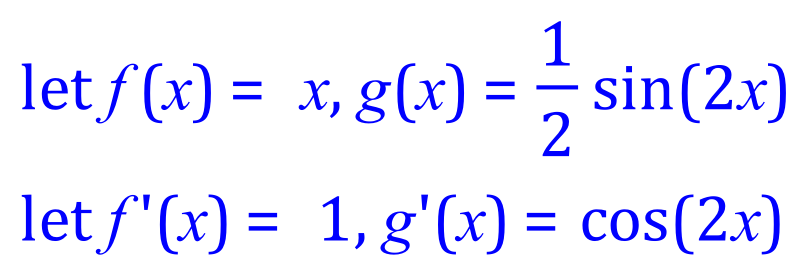
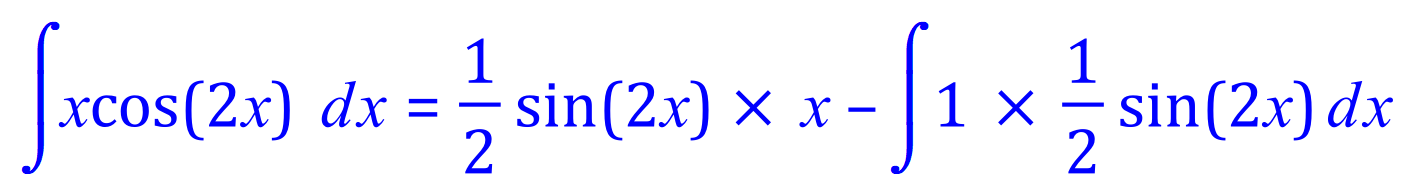
Rearranging, and taking account of the constant multiple in the second integrand:
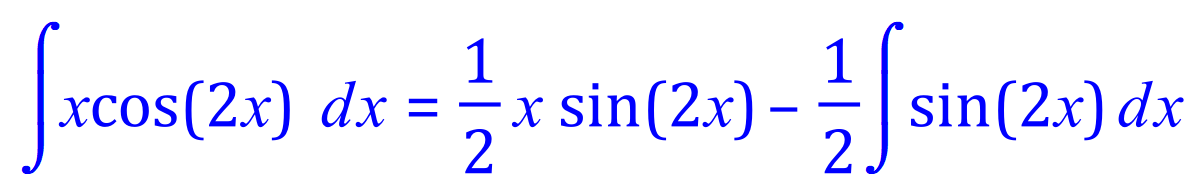
Integrating the second expression:
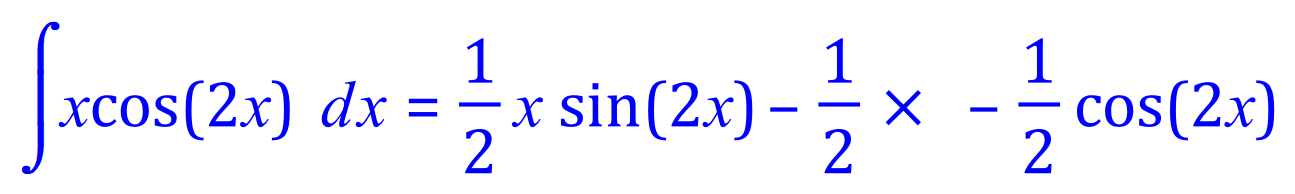
Rearranging:
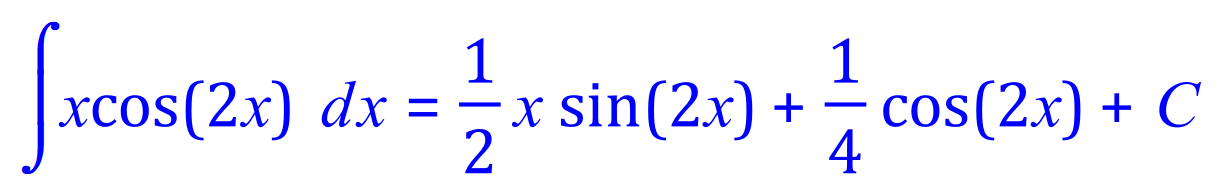
Q6. Integrate, using the integration by parts method, the following expression:
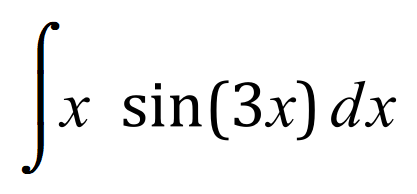
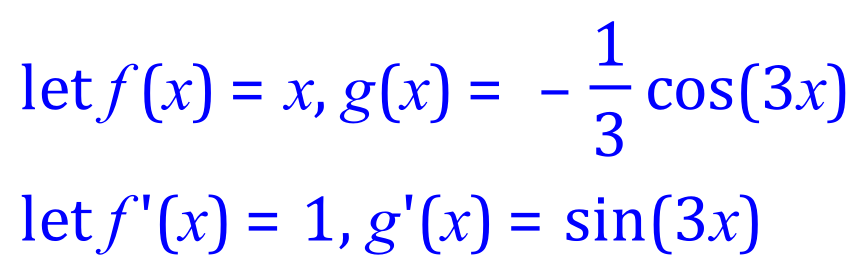
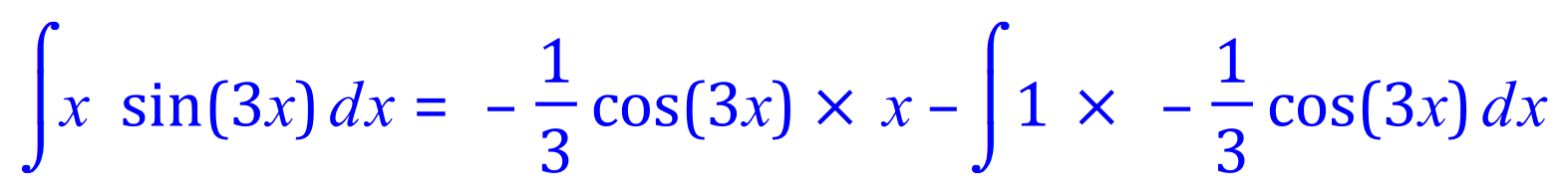
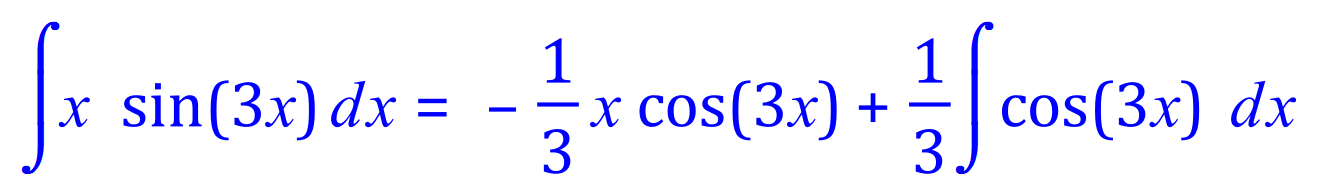
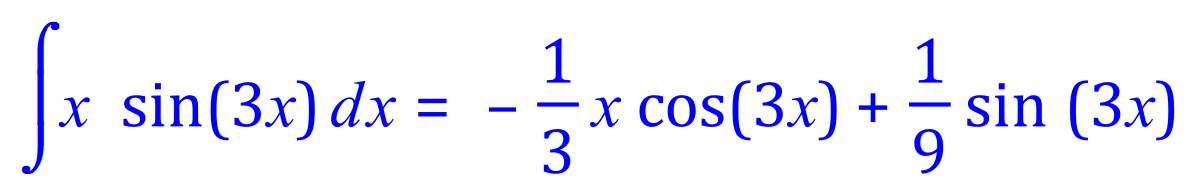
Usually rearranged (don't forget the constant of integration):
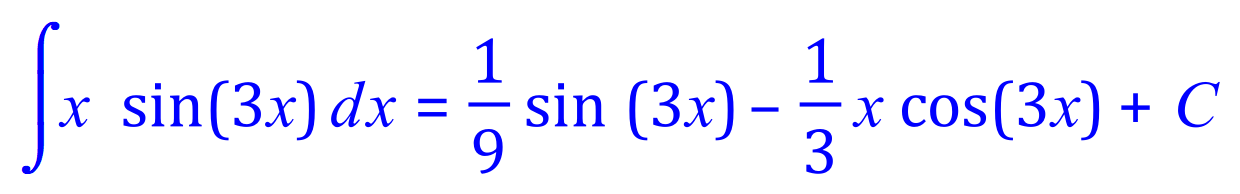
Q7. Integrate, using the integration by parts method, the following expression:
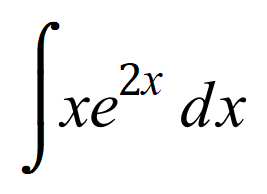
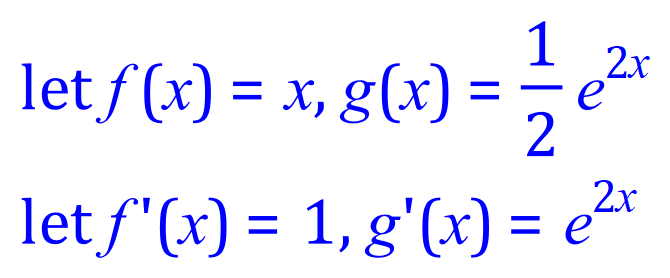
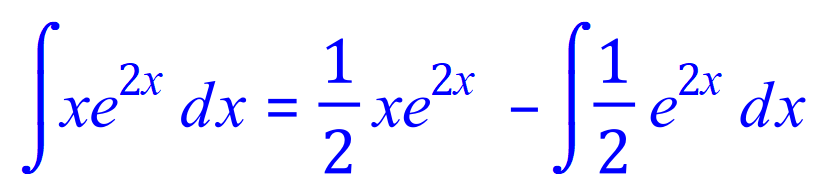
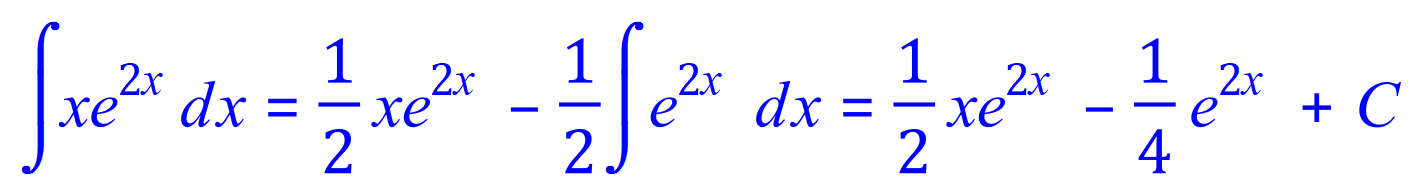
It is usual to simplify any "final" expression if possible, so:
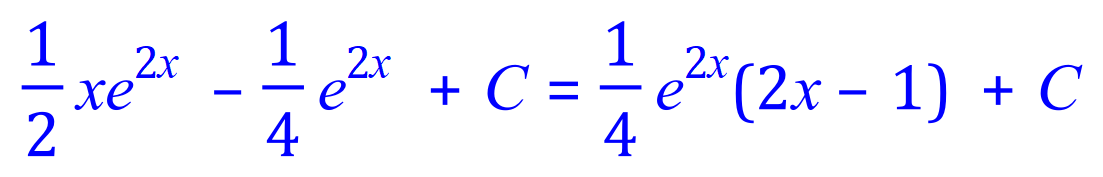
Q8. Integrate, using the integration by parts method, the following expression:
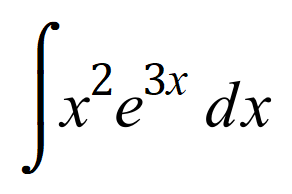
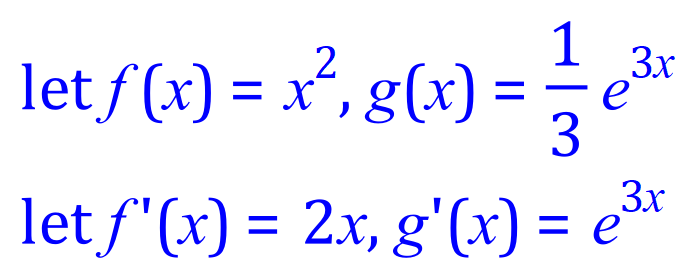
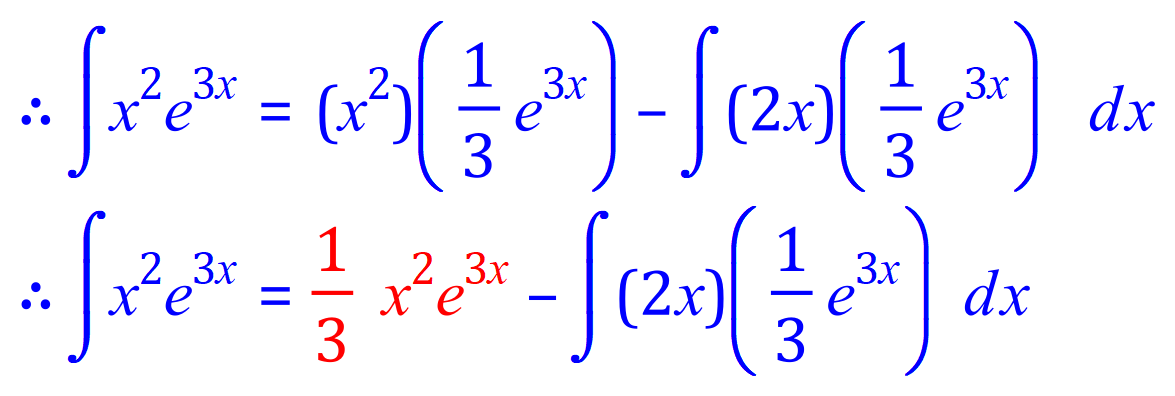
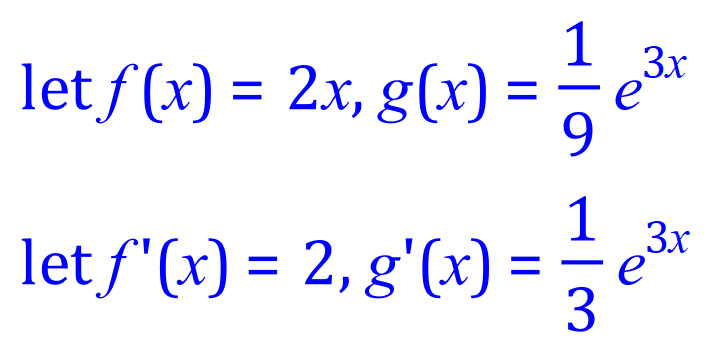
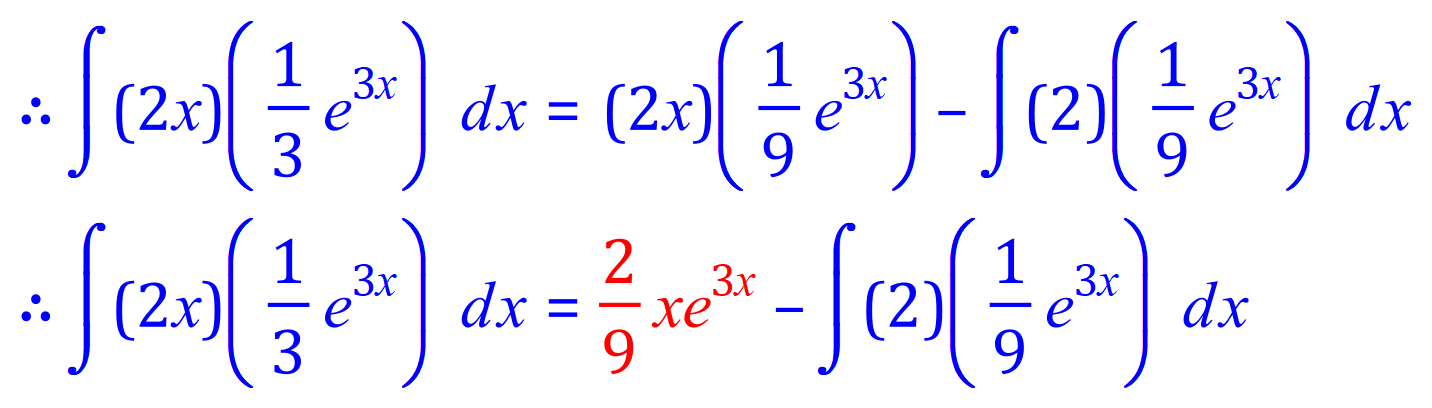
** Now:
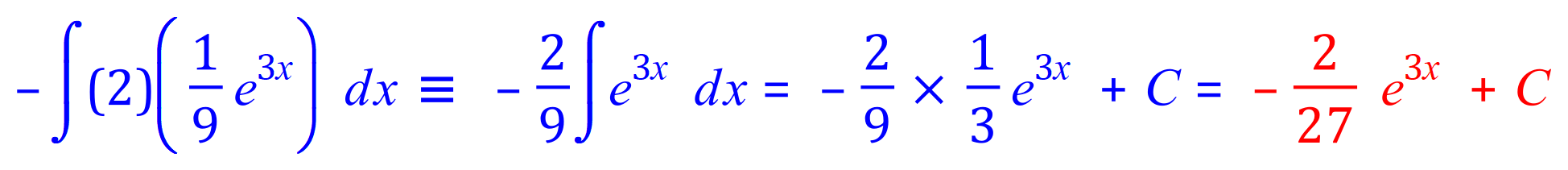
FINAL RESULT:
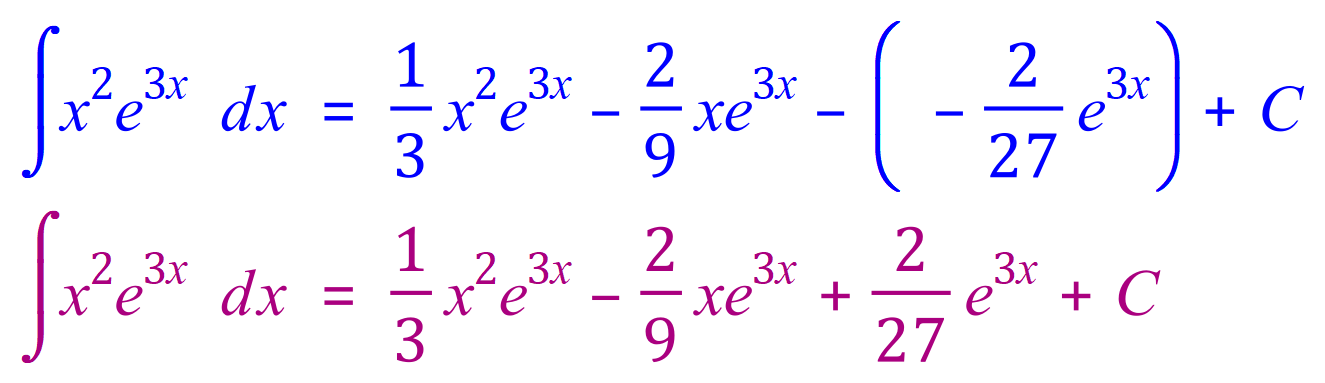
** Pay particular attention to this line, and the last 2 lines, where the - (- becomes + as a result of the constant "2" being removed from the integral by the constant multiple rule, ending up in -2/9 multiplied by 1/3 giving an overall negative result which is then subtracted, and "a negative minus a negative is a positive".
Back To >> Questions <<
Back To >> Integration By Parts <<