[A] Integration By Substitution
Sometimes, in integral calculus, it is easier to make the integration by first of all substituting a complicated expression for a simpler one. Because this substitution very often involves the lowercase letter ‘u’ (for no other reason, as far as I can see, other than a mathematical convenience), you will sometimes see this referred to as “U substitution”.
Look at the basic indefinite integral below:
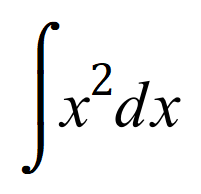
We already know, from our previous involvement with integration that the way that we integrate this is to add one to the power and divide the resultant expression by the new power:
Therefore

But what happens if we have an expression like this?

How do I deal with this?
Well clearly there’s nothing stopping you from multiplying out the brackets and then performing basic integration on the result:
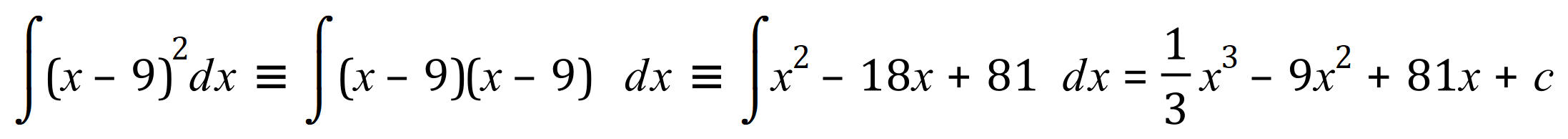
Of course when the powers start to get larger, the expansion isn’t quite so straightforward and although it probably isn’t difficult it can be very messy with a greatly enhanced probability that you will get at least one of the signs wrong somewhere along the line resulting in a completely wrong solution. Just take a look at the cube expression:
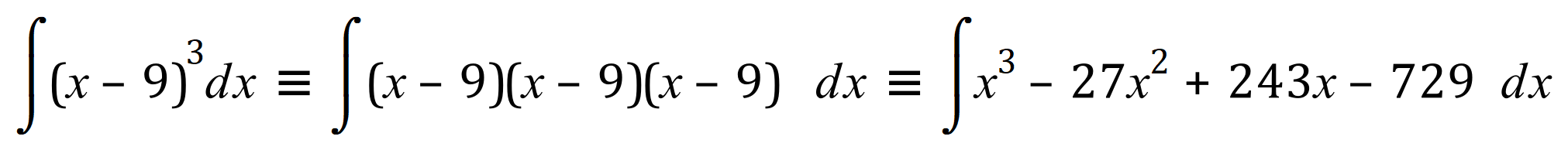
Now without even performing the integration, I can see that this is going to be a nightmare, already we are into cubic powers!
Even worse…….

Just the expansion will keep you awake all night!
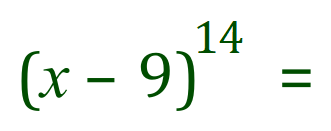

Do you really want to integrate this? - I didn’t think so!
Surely there must be a better way than this? Enter… Stage left… “U substitution”
Consider once more our basic integration:

This time we will substitute for the contents of the brackets, the lowercase letter “u”
Our expression then becomes:
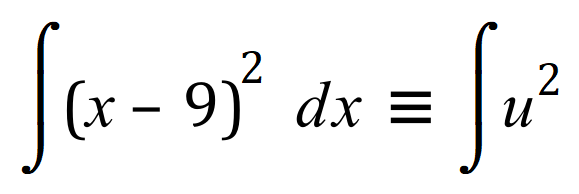
At this point we perform the basic integration just as if “u” was in fact “x”
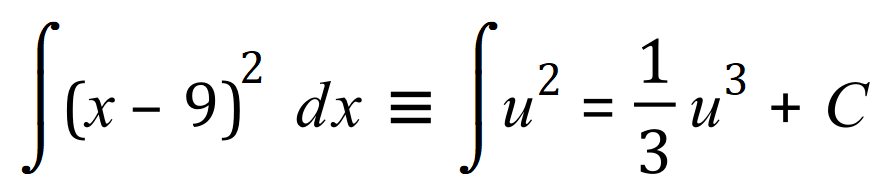
The final step is that we now re-substitute our previously substituted expression involving ‘x’ into the result, therefore the final answer will be:
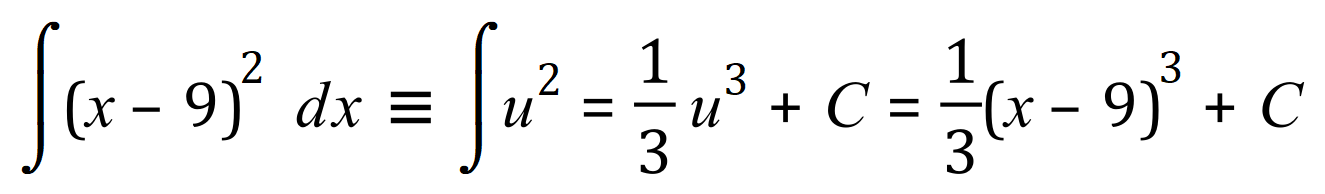
Okay let’s go back to our horror story involving the 14th power above:


A lot simpler this time isn’t it?. U substitutions can also be used in mixed expressions involving trigonometric and polynomial expressions.
Consider the expression:
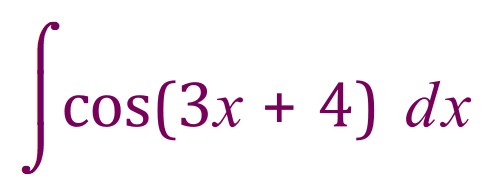
The way we approach this problem isn’t quite as clear-cut until we realise that we can in fact substitute the contents of the brackets, perform the integration and then substituted back for ‘x’
![]()
The expression above then starts to translate into terms involving ‘u’
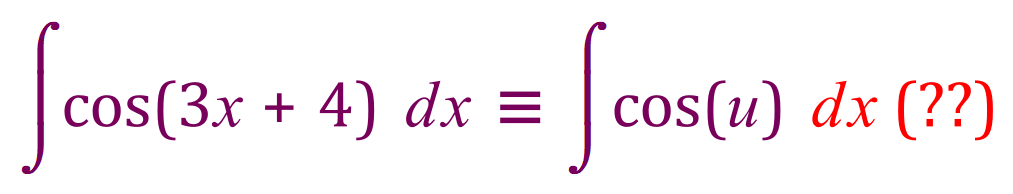
Hang on!
This doesn’t make sense does it? How can we integrate ‘u’ in terms of ‘x’, well we can’t so what we have to do is ‘amend’ 'dx' to reflect the fact that we now must integrate in terms of ’u’
Since we have already substituted:

Then it follows that
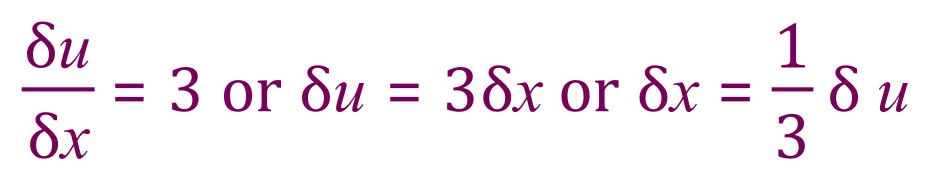
Although it probably isn’t entirely correct mathematically to say what I’m about to say, it can make the next step a little bit easier to follow. Now that we have established the last expression involving ‘dx’ we substitute this where we find ‘dx’ above, so expression becomes:
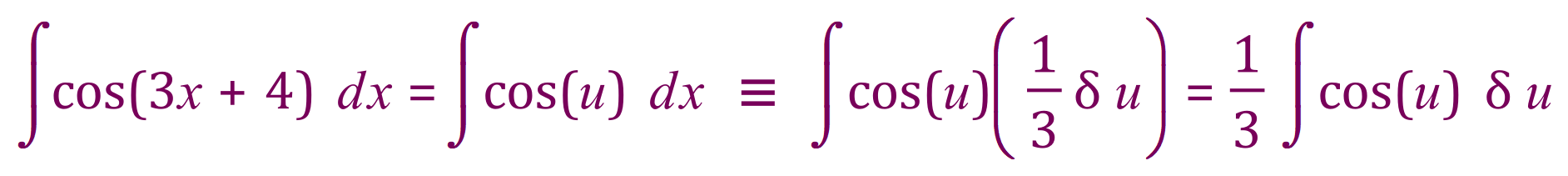
Now we have a straightforward integral in terms of ‘u’ which we integrate in terms of ‘u’ applying the constant multiple rule where the fraction one third is involved:
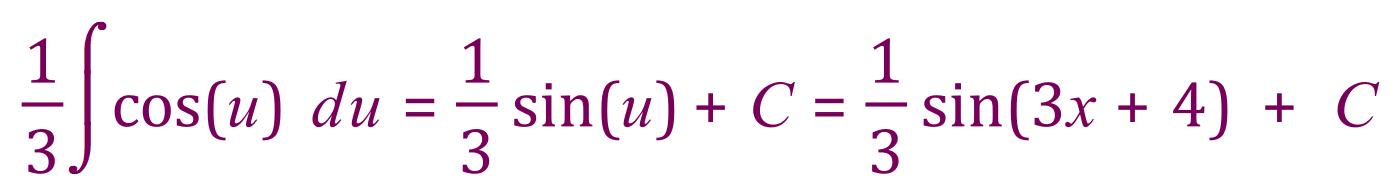
Let’s try another example:
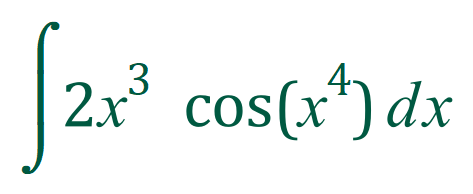
This looks a little bit more menacing but in fact if we apply the same rules, taking each step slowly and logically we will arrive at a correct solution with the minimum of fuss and panic.
What you have to remember is that when you make your substitutions for ‘x’ you must also make an appropriate substitution for ‘dx’
![]()
Our intermediate stage, which isn’t correct in its entirety will now be:
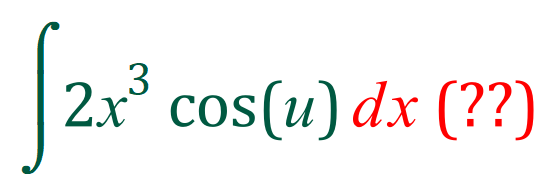
But now we have to remember to substitute appropriately for dx:
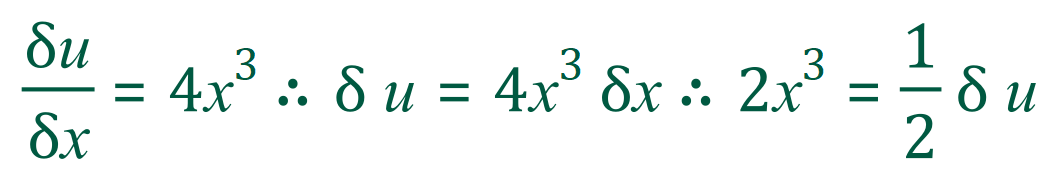
If you re-substitute into the expression in the first bullet point above:

The right-hand end of this expression is now an integral we can simply integrate:
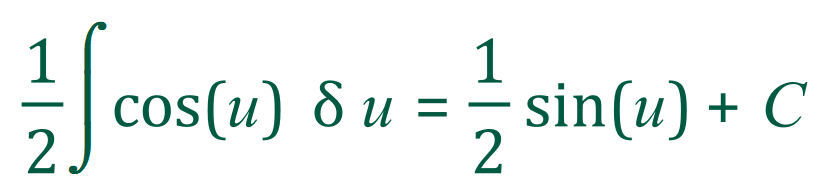
And if we substitute back for ‘u’ we arrive at the solution:
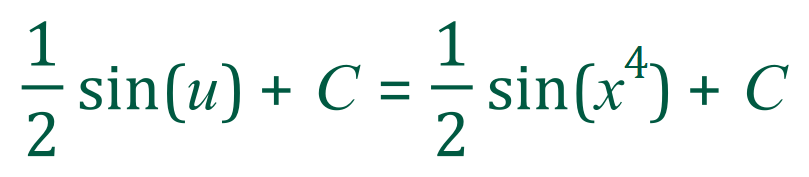
OK we will now go through one more example just be absolutely sure that we know where we’re going:
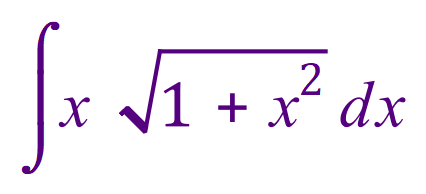
Eeeughh.....I can hear you say, how do we deal with the square root? Well in fact the square root is only a power as you know so we will be able to deal with it when the need arises by changing the “square root symbol” to the power “one over two”.
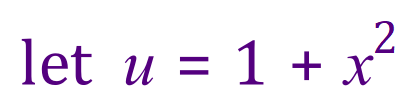

So….
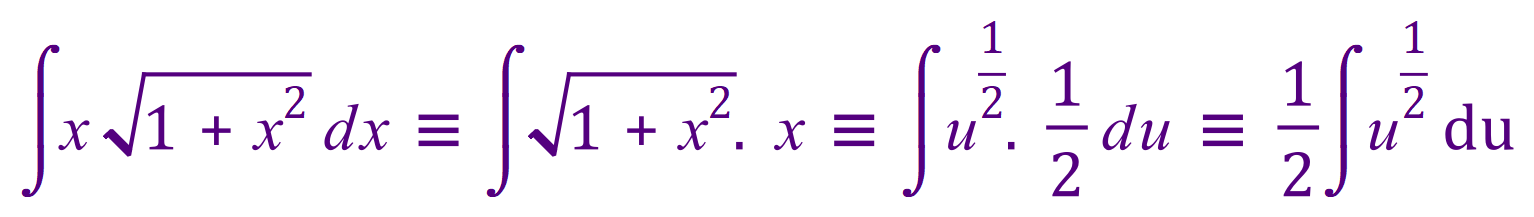
You may need to study the line above because I have made some rearrangements and some substitutions all in one go. What I have ended up with is an integral that can be solved quite simply.
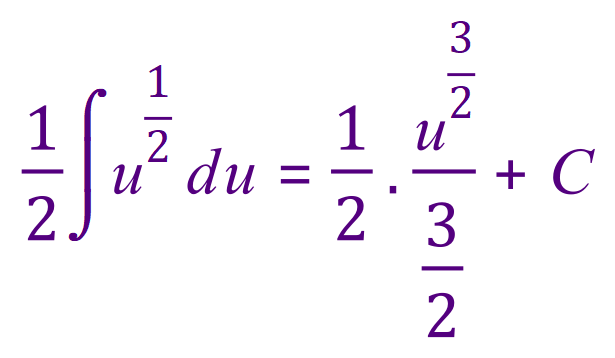
Try to remember that the dots that I’ve placed in this expression are meant to signify “multiplied by” because inserting anything that looks remotely like a cross would only confuse in this context.
Tidying up the extreme right-hand side of the confusingly messy above expression gives us:

And re-substituting for ‘u’… gives us the final expression:
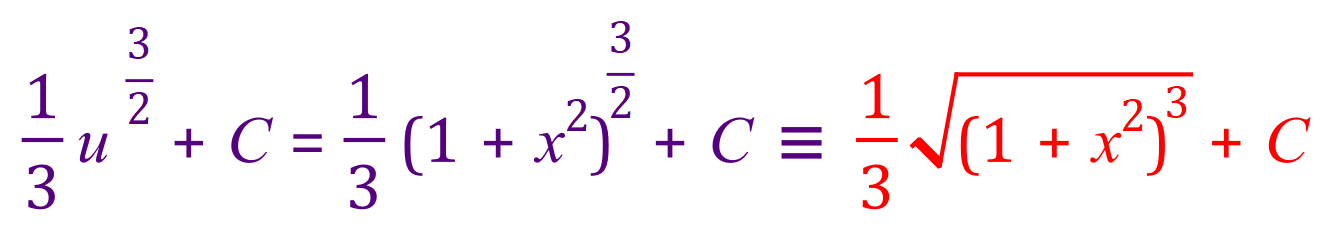
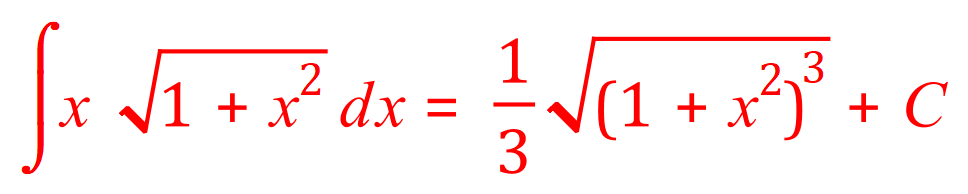
Replacing / reinstating the square root symbol isn’t really necessary in the last step, all it is doing is showing that you have the knowledge that the power “three over two” actually means “the square root of the object cubed”. I doubt very much if it would give you any more marks in the question.
>> Questions <<
Go To >> Table Of Standard Derivatives And Integrals <<