Q1. Integrate by substitution or an appropriate method the following indefinite integral:






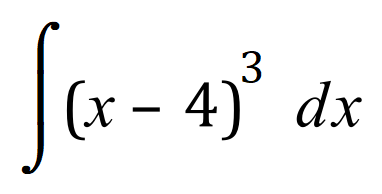
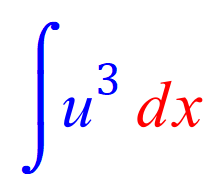
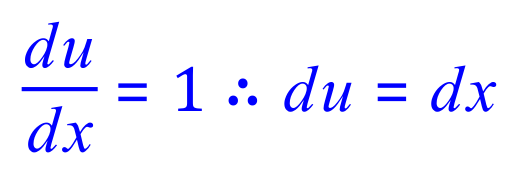
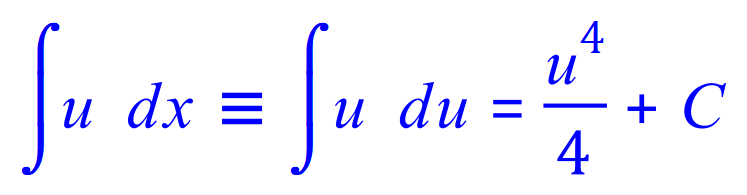
FINAL ANSWER:



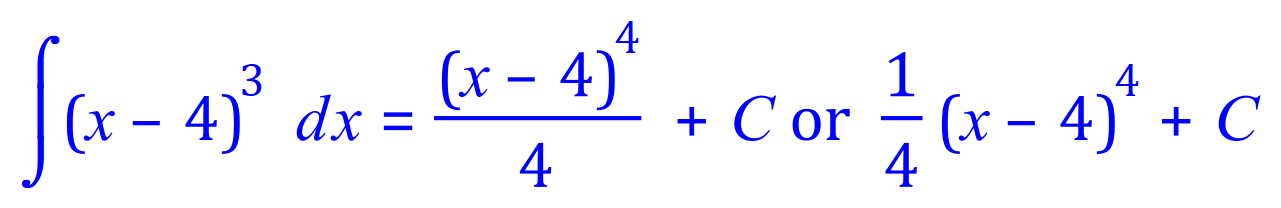
Q2. Integrate by substitution or an appropriate method the following indefinite integral:








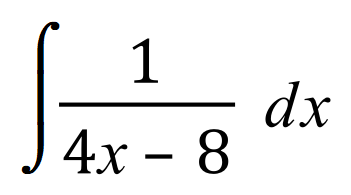
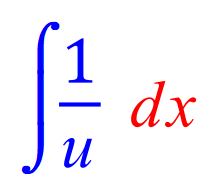
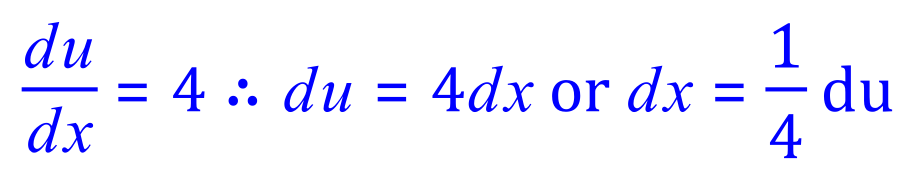
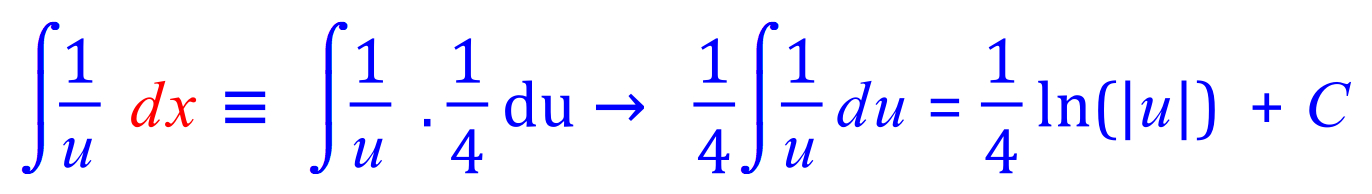
FINAL ANSWER:



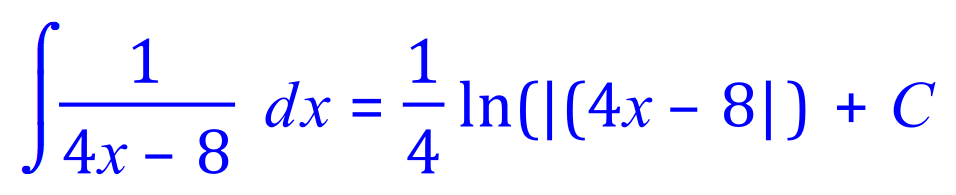
Q3. Integrate by substitution or an appropriate method the following indefinite integral:



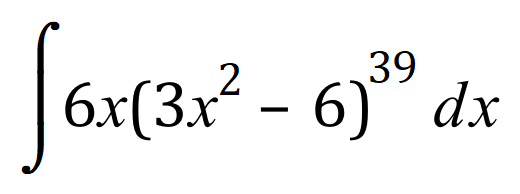
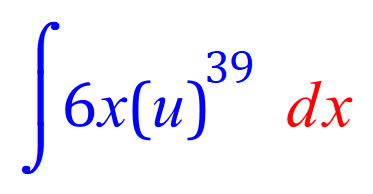
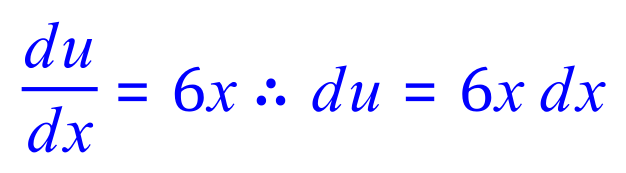
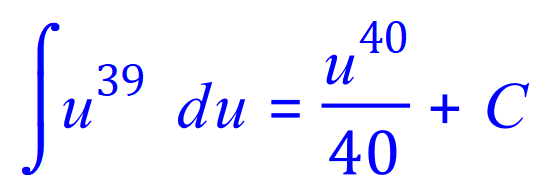
FINAL ANSWER:



Q4. Integrate by substitution or an appropriate method the following indefinite integral:


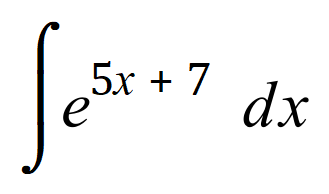
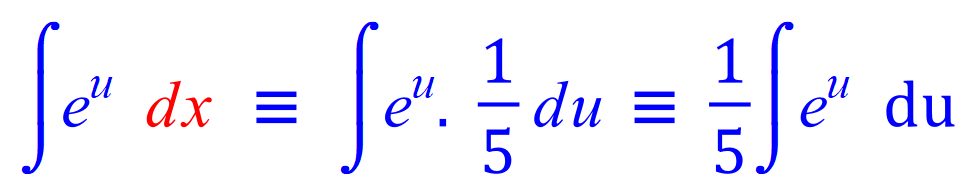
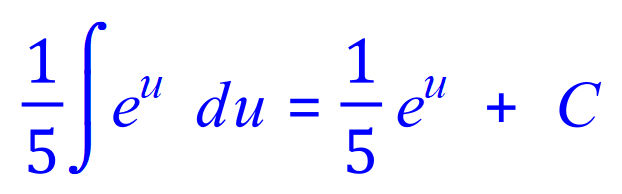
FINAL ANSWER:




Q5. Integrate by substitution or an appropriate method the following indefinite integral:


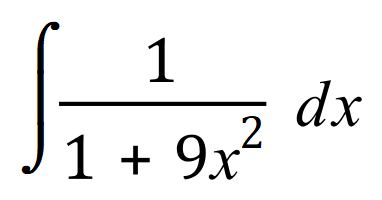
You may have noticed that I have put the link to the list of common derivatives and integrals on pretty much every page in this section. This particular question will probably lead you to look at them. The format of the question is not unlike the standard integral with the result containing the arctan or tan-1 function, Suggesting that somewhere in the solution this function will reside. You won't be wrong :-)



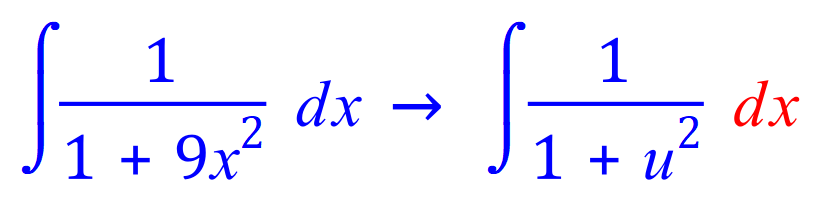
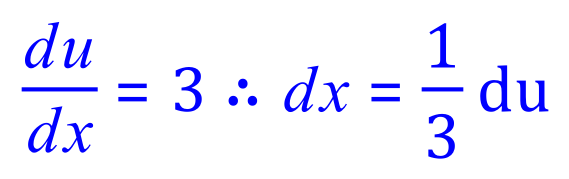
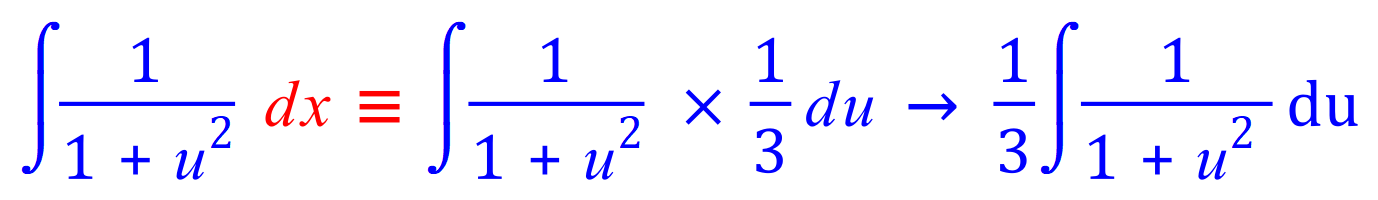
We now have a fairly straightforward integration to complete, in terms of 'u' and application of the constant multiple rule. If we look at the table of standard derivatives and integrals we will be able to see that our fractional expression involving u2 has the standard integral:

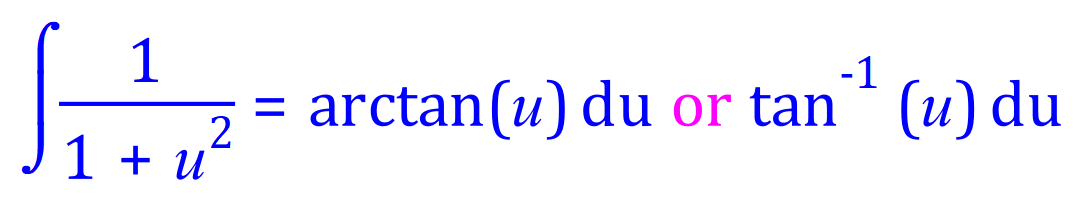
Therefore if we substitute this expression into our newly arrived at integral in terms of 'u' :


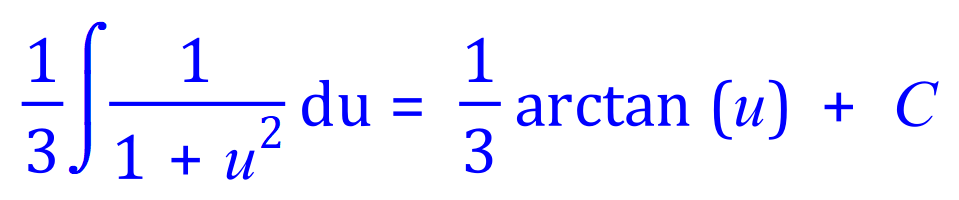
FINAL ANSWER:

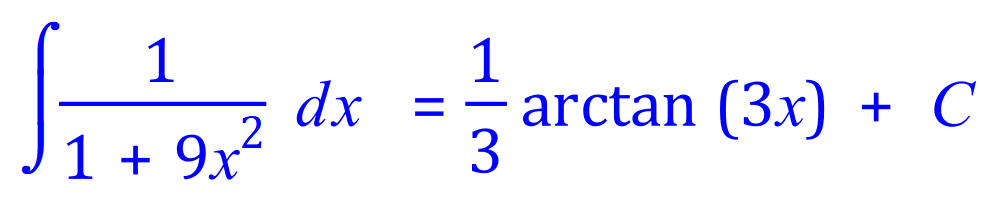
Back To >> Questions <<

Back To >> Integration By Substitution <<

Go To >> Table Of Standard Derivatives And Integrals <<