[A] The Doppler Effect
In each case the equation is given in the graphic above:
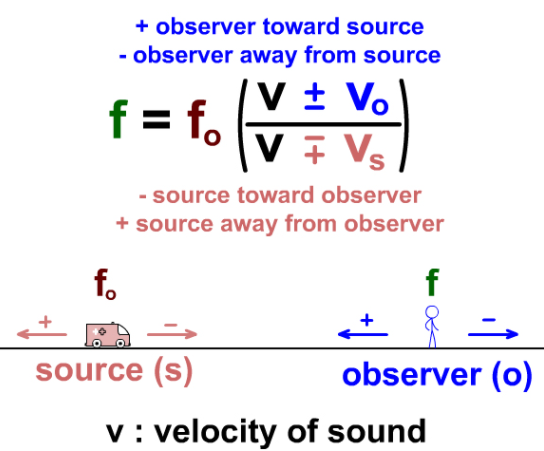
Q1. As in the example given in the text and the diagram above, an emergency vehicle sounds a siren with a frequency of 800Hz, the speed of sound in air is given as 343 m/s. From this information calculate the perceived frequency of the siren from the perspective of the observer if the vehicle is approaching at 30 m/s.
A1. We are given a base frequency fo of 800Hz, a velocity vs of 30 m/s and a velocity v of 343 m/s. The observer is stationary (as there is no evidence to suggest otherwise). The velocity v is not adjusted either way because of this but we must remember to subtract the source velocity from that of the velocity of sound in air:
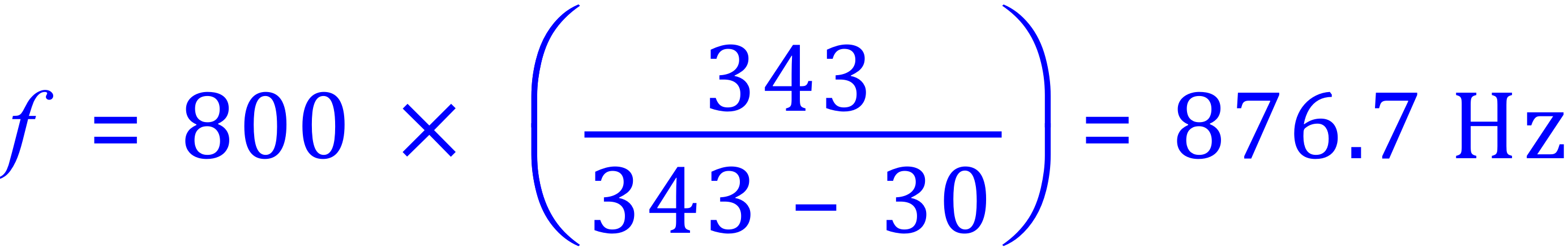
Q2a. What is the frequency heard by a person driving at 15 m/s toward a blowing factory whistle (800.Hz) if the speed of sound is 340.6 m/s?
A2a. Again look at what we have been given. fo = 800Hz, v=340.6 m/s, vo = 15 m/s and obviously vs = 0 m/s (factories don't tend to move much!)
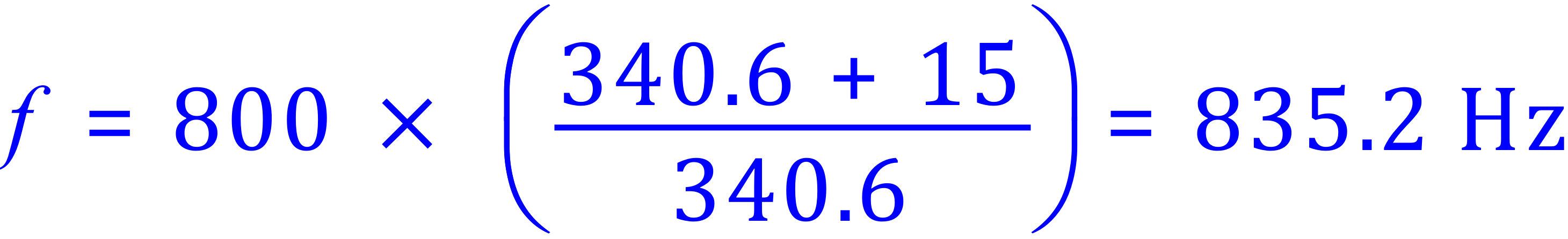
Q2b. From the previous problem, what frequency would he hear after passing the factory if he continues at the same speed?
A2b. This time the source is being moved away from, the velocity of the observer is 15 m/s away from the whistle with all other values the same:
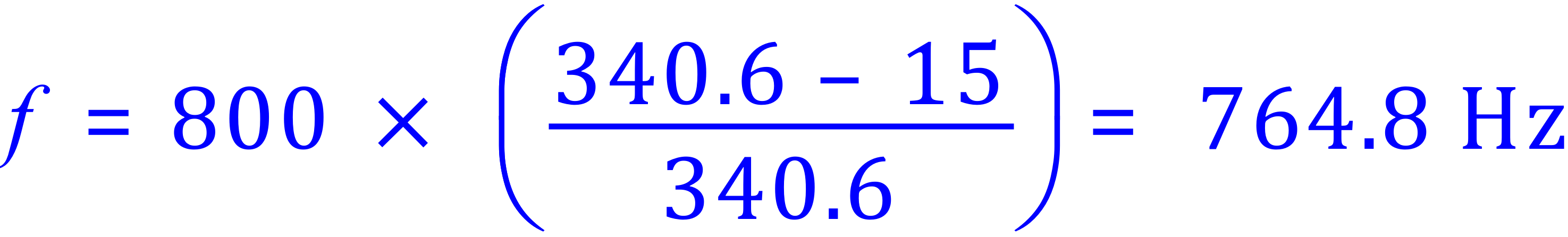
Q3. You are riding a bicycle along the road at 15 km/h, going in the same direction as an ambulance which is approaching you from behind at 60 km/h. You can hear the 700Hz siren of the ambulance behind you as the ambulance approaches you. What is the change in sound frequency after it passes you, if the speed of sound in air is 343 m/s?
A3. This is slightly trickier because we have to convert km/h to m/s. Go ahead and confirm this if you like (good practice) but if not ..... 15 km/h is 4.2 m/s and 60 km/h is 16.8 m/s.
Step 1 - on the approach to you:
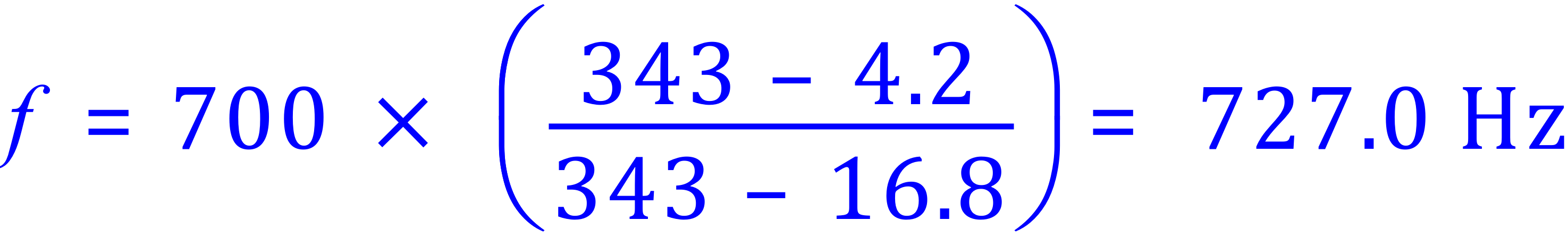
Step 2 - when the ambulance has passed you:
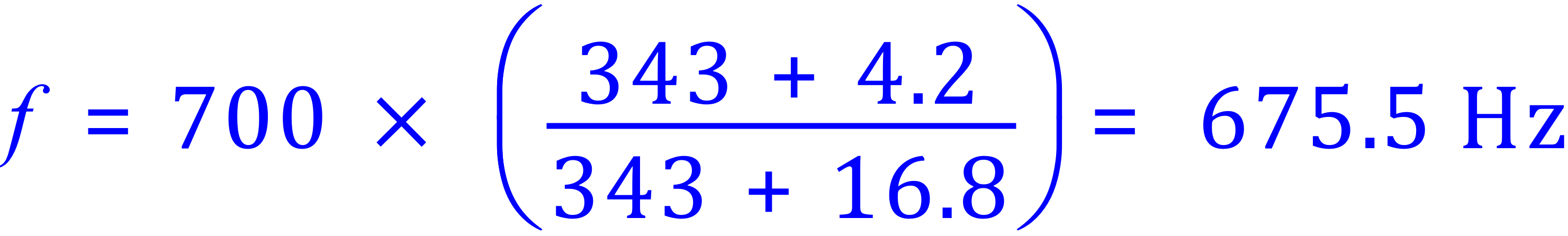
The difference is 727.0 - 675.5 = 51.5 Hz
Back To >> Questions <<
Back To >> Doppler Effect <<