Algebra and The Four Basic Operators
“Why should I learn Algebra? It’s not like
I’m ever going to go there!”
A standard joke by many comedians, algebra is probably one of the most misunderstood areas of mathematics yet it has a beautifully pure logic attached to it.
Algebra is about “unknowns” or more correctly, “variables”.
The name “algebra” comes from the Arabic al-jabr which means “reunion of broken parts” and in its elementary form uses letters in the place of numbers to represent the above mentioned variables.
You have probably already met algebra without in fact knowing it, if you have used any formula where you have been required to enter numbers to obtain an end result then it is almost certain that your formula could be properly regarded as an “algebraic expression”.
Take for example the simple equation that we all learn in infant school when we first start arithmetic:

We have no variables here, “1” has a fixed value as does “2”, the values never change, that is they are constant and so logically they are referred to as “constants”, whereas variables above represented by letters can have literally any value.
Consider the first algebraic restatement of the above expression:

Of course we know straight away that the value of ‘x’ is one, but how did we get there? Take a look at the “= sign”:
For any equation to retain its “equality” both sides must represent the same value, in other words they must be equal. In the picture shown if the two blue weights were taken away from the left-hand side then to retain the balance two of the grey weights would have to be taken away from the right hand side.

This leads to our first rule “anything done to one side of the equation must be replicated on the other side if the balance is to be maintained”. So, going back to our equation, we can obtain the value of ‘x’ by doing the same thing to both sides…that is…take 1 away:

We removed 1 from each side to reveal a value for ‘x’
Let us look at a slightly more difficult example, but one that we can solve just as easily:
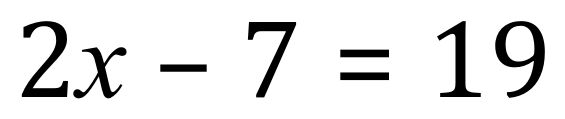
OK, not exactly a ‘one and one’ type of equation but to solve it involves only two simple steps:
1. Add 7 to each side:
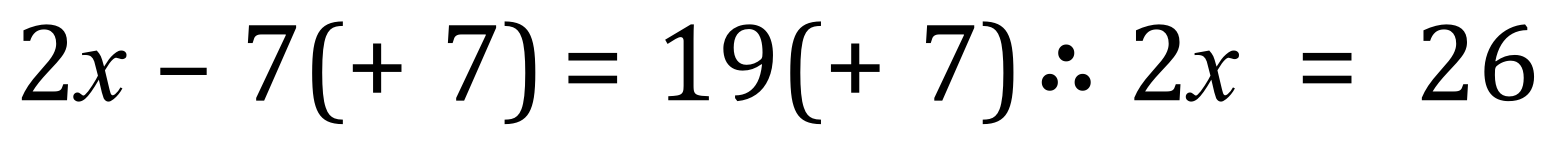
2. Divide both sides by 2:

Simple enough?
Effectively you are “rearranging the equation to get the variable quantity ‘x’ on its own on one side”, and as you get better at this you will find that you can perform the steps to do this automatically without having to write them down individually, and in some simple cases in your head!
OK what about this one?
![]()
Well…just do the same as before:
Add 12 to each side
![]()
Now multiply each side by -1
![]()
Divide each side by 6
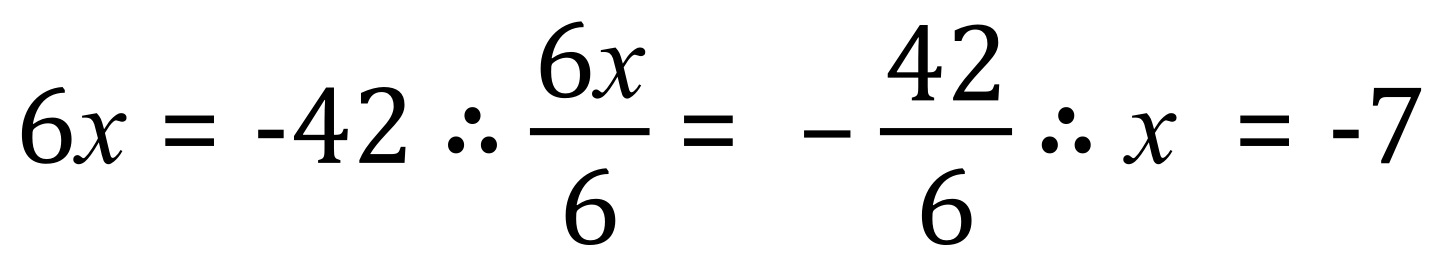
It is a good practice to ‘substitute for x’, that is, put your new found value for ‘x’ back into the equation to see if it is right:
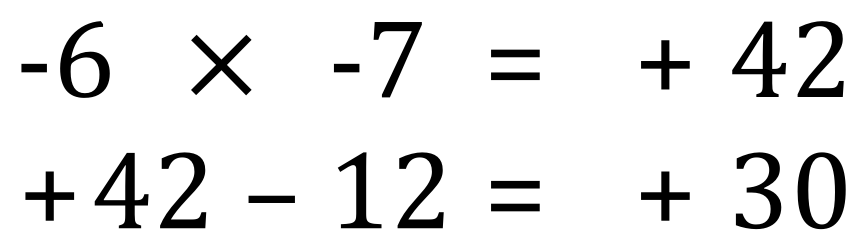
More than one variable?
This can present a problem, take two variables ‘x’ and ‘y’:
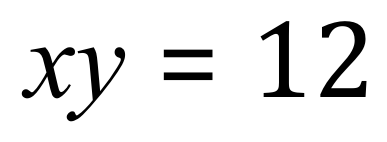
This means “x times y equals 12” but how do we work out the values of x and y? Well as things stand we can’t, because ‘x’ and ‘y’ could have infinite variable values, for example x=1, y=12 or x = -24, y = -½ and so on.
We can usually work out ‘representative’ values for mixed variables when they are on opposing sides of the equality. Use the method above, divide both sides by 2 to leave:
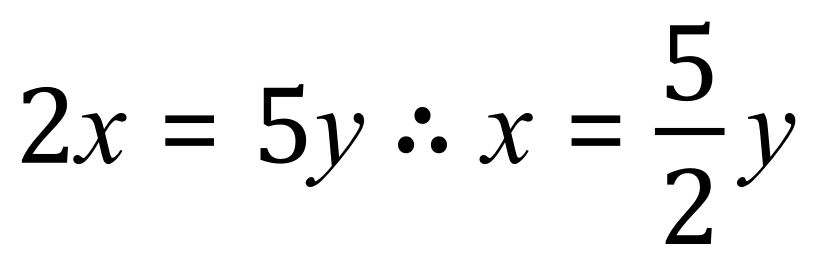
Or divide both sides by 5:
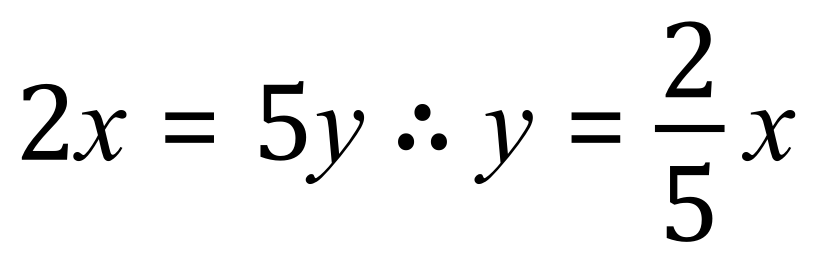
But these answers are only representations of each variable in terms of the other, to be able to find out the values of two separate variables, you would need two equations and would have to solve them simultaneously (this sort of action will be seen in another section, when we do indeed start to look at “simultaneous equations”).
We will now look a little bit more at these variables, and at ways in which we can manipulate them using the four basic operators and powers.