Algebraic Multiplication
A slightly tidier operation than addition or subtraction because the end result can usually be simplified or “tidied up”:
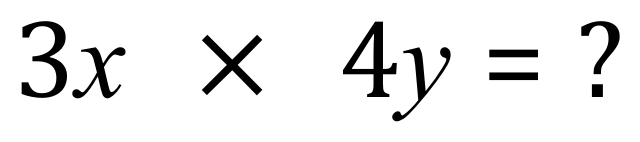
The answer to this little problem is “three times X times four times Y”. Now we can multiply the constants together to make 12 but what can we do with X and Y? Well, all we can do is put them together like this:
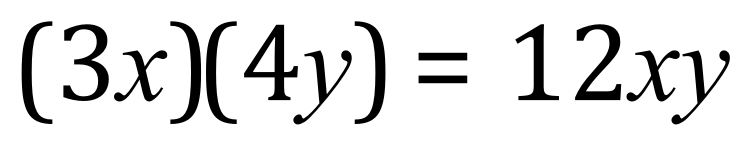
In mathematics when you see sets of parentheses back-to-back it means multiply, so in the above example 3X will be multiplied by 4Y and it will be this representation that we use in the rest of this document. As can be seen 12XY is the answer and cannot be simplified any further.
Try substituting some values for X and Y and you will see that the above equation is in fact correct.
When we have the same variable type, ie: just 'x' or just 'y' we start to look at using power notation. In the example above:
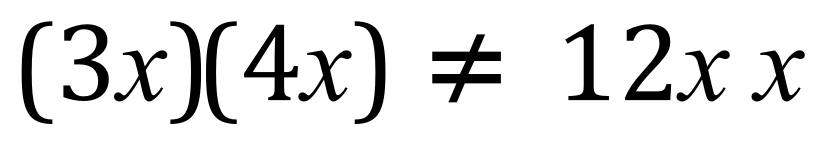
I have used the symbol "not equal to" only to show you that the answer would not be represented in this way. In fact, if you look carefully at there is a small gap between the two 'x's on the right-hand side, this is a result of the software that I'm using attempting to correct my error! When we have variables that are the same, power notation or index notation is used therefore in this case we would write the answer as 12x squared:
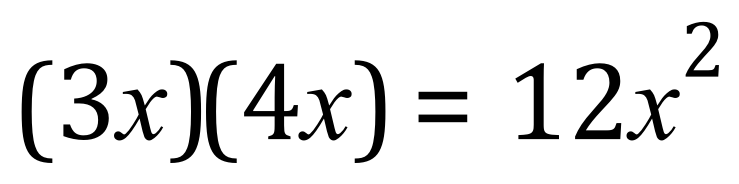
The rule here is quite simple, when you can collect like terms use index notation to represent them, any differing terms will simply have to be grouped together as in the "12xy" example above.
Q. Simplify:
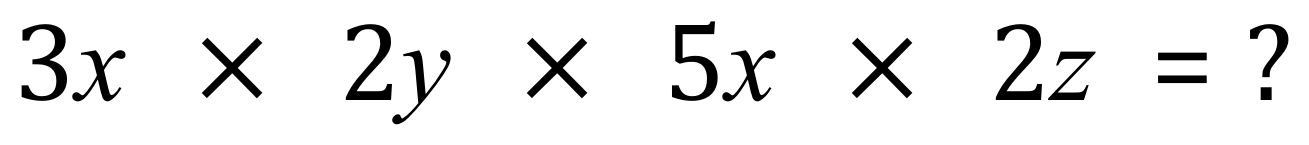
A. Sometimes it can help you to collect your like terms before you start looking at any multiplications, although this is a fairly straightforward example they can become quite difficult.
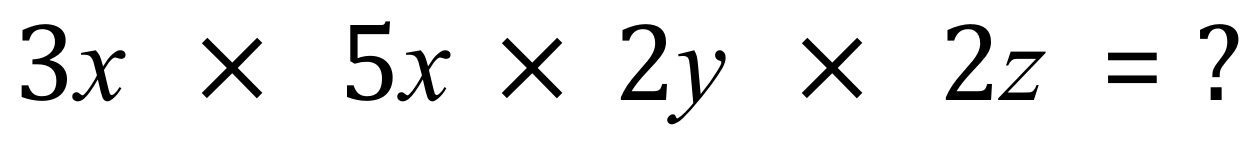
The first step is to multiply together all of your coefficients (that is the numbers preceding each variable), so in this case we have 3×5×2×2 which is 60:
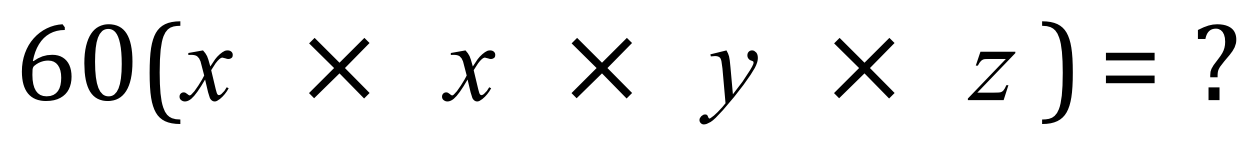
It is quite normal here to take the 60 out of the brackets and group the variables inside the brackets. Now we need to multiply the variables together, and you should be able to see that we have "x squared yz":
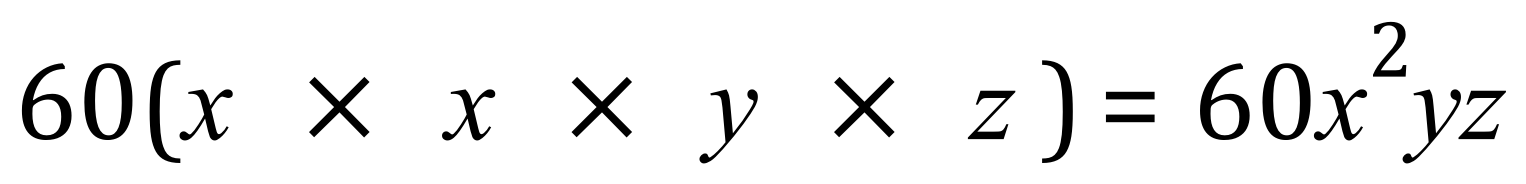
If you want to "back check" to make sure that this is in fact correct, just give your variables some simple numbers for example, let 'x' = 1, 'y' = 2 and 'z' = 3:
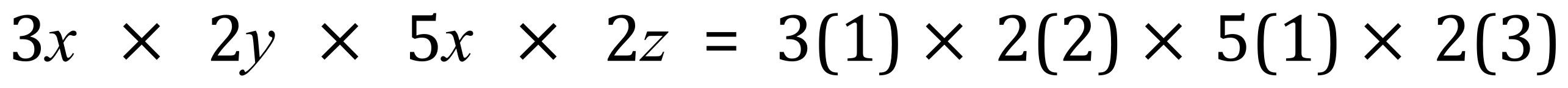
So:
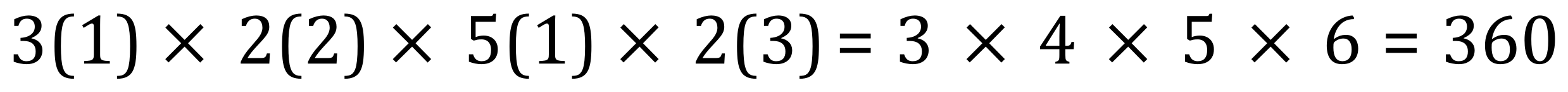
And:
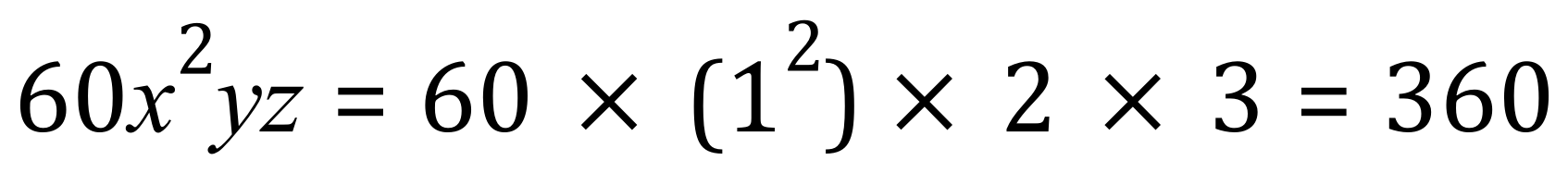
Q. Simplify:
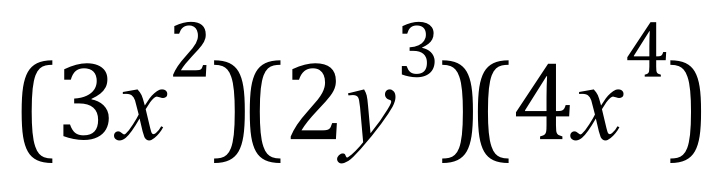
A.
Group all of the variables according to type, multiply out the coefficients and add up the index notations where applicable:
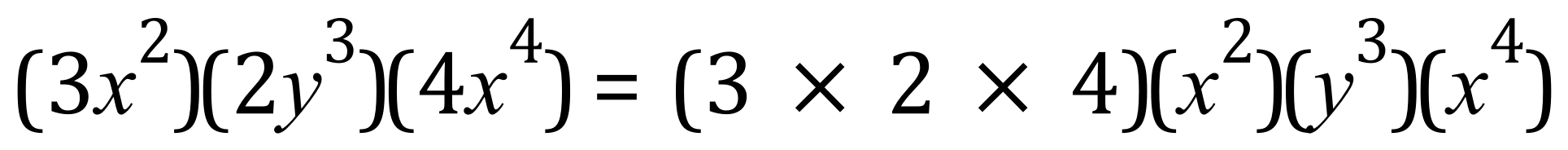
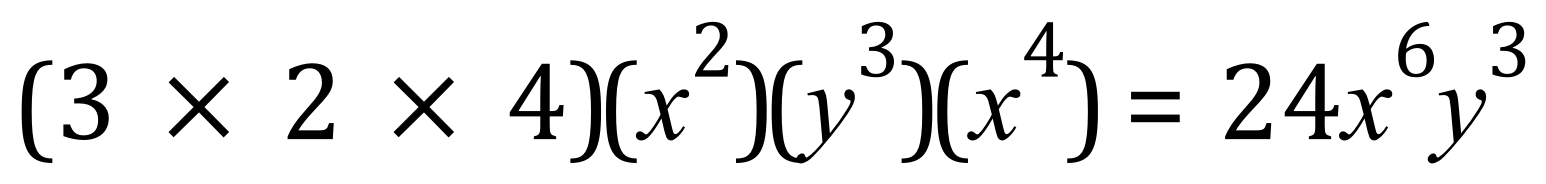
Q. Evaluate the below expression:
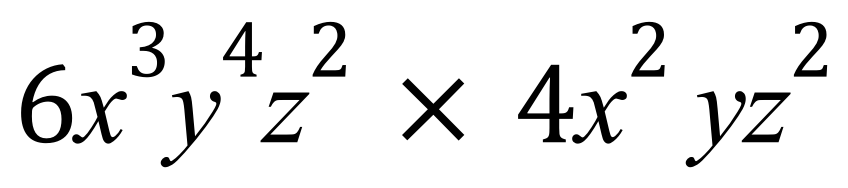
A.
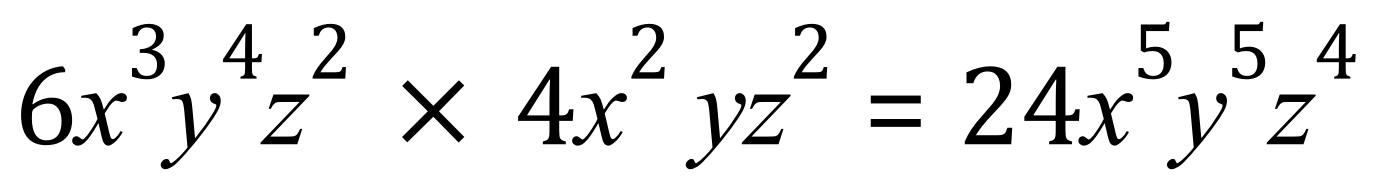
This can be checked if we assign numerical values to x,y and z. Let us call x=2, y=3 and z=4:
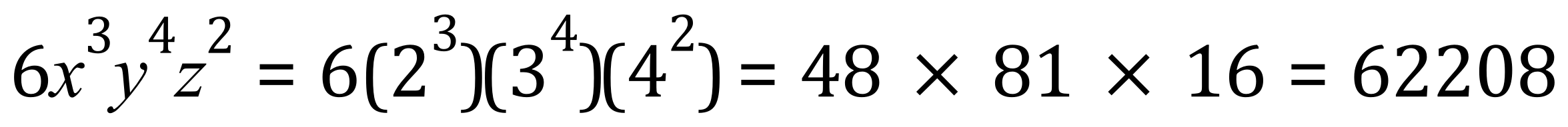
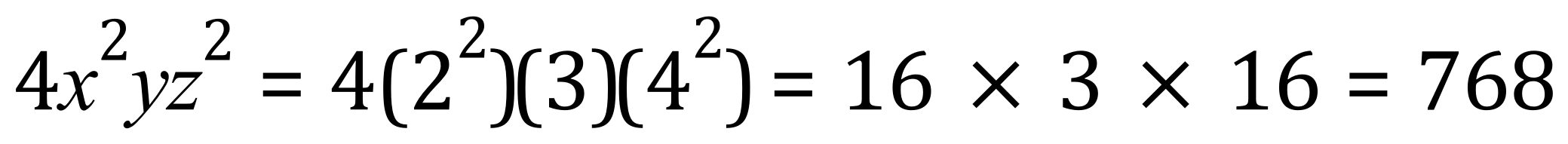
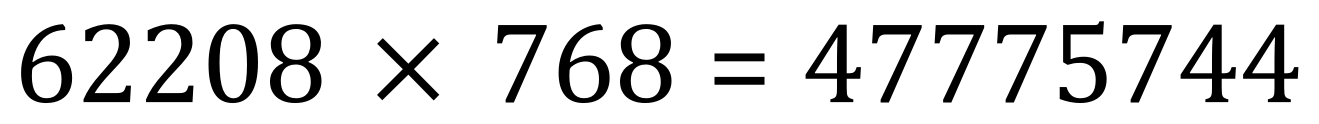
And....
