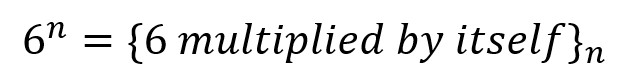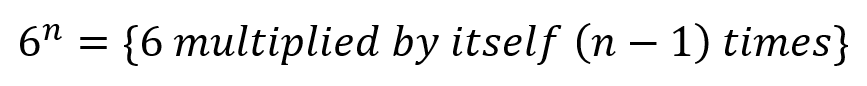Appendix M1 - Representation of Units (Index Notation)
You have probably come here to see what the difference is between unit representations eg: g/dm3 and gdm-3
You might be thinking to yourself "well what's the difference?". They both mean the same thing, it is a mathematical representation using index notation in the second example. This is something I think you need to get to grips with because you may see these interchangeably during your studies of science, in particular advanced chemistry. We will now go off (no pun intended) on a short tangent into the world of mathematics, to explain where these representations actually come from. First of all we will look at index notation.
In the table below I have written 7 numbers, each number is 10 times the previous one, say for example 10 is 10 times larger than one, 100 is 10 times larger than 10, 1000 is 10 times large than hundred and so on up to 1,000,000. It is important to notice how many zeros each number contains, and in particular please take notice of the fact that number 1 contains no zeros, this is quite relevant!
|
1 |
10 |
100 |
1000 |
10000 |
100000 |
1000000 |
Let us choose the middle number of our range, we will look at the number 1000. This is a single number 1 followed by 3 zeros. it can become unwieldy when the numbers get bigger and bigger to have to keep writing out the numbers of zeros, and it would be very easy to get it wrong and either add too many or not enough. We use a shorthand notation, by putting the number of zeros as a single digit in superscript to the top right of the number, so for example the number 1000 would be "10 raised to the power of 3" and it would be written this way:
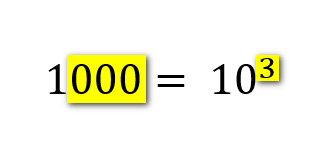
We count the number of zeros and put a superscripted number 3 to show that 1000 is "10 raised to the power of 3" or "one followed by 3 zeros". What do you think it would look like if we did the same to 1,000,000?. If you said that it would be 10 to the power of 6, that is one followed by 6 zeros and shown like this......
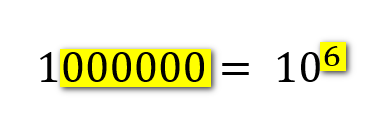
......then you would be quite right!
It is only a tiny little bit more complicated when we start to look at fractional powers, for example we have seen what "1000" is, but what is "1000th" that is....... 1 / 1000 ?
First of all, let us take a look at what "one thousandth" looks like is a fraction:
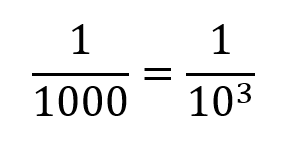
I'm sure you can see that one divided by 1000 is the same as one divided by 10 to the power of 3, and this works the same for the others such as 1,000,000 which would be one divided by 1,000,000 or one divided by 10 to the power of 6. To represent this fraction we can also say the following:
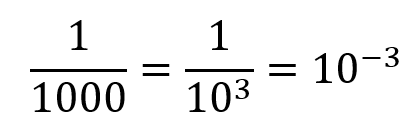
So just as 1000 is 10 to the power of "+3", we can see that one thousandth (1 divided by thousand) is 10 raised to the power of "-3". This works for other numbers as well as tens, and I will detail a few examples in a moment. Before this, I want to go back to the number box above and look at 100, 10 and finally 1.
How many zeros does 100 have? Well of course the answer is "2" so we can represent 100 as 10 "to the power of 2", similarly the number 10 itself has "1" zero so we can refer to this as 10 "to the power of 1". So what do we say about the number 1 itself? Can we say (because it has NO zeroes) "10 to the power of 0?". Well, take a short break and put 10 to the power of 0 into your calculator and see if it actually gives you the result of "1".
You should find that it did:
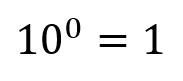
Without making this a particularly deep mathematics lesson, I want to move now to numbers other than 10. Just for an example I am going to use the number 6 and show you what we have if we raise 6 to a positive or a negative power in just the same way that we have done for 10 above. So let's get started with, say for example 6 raised to the power of 2:
you probably know that 6 raised to the power of 2 is also known as "6 squared" and has a value of 36:
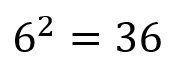
6 "raised to the power of 2" is actually 6×6, 6 "raised to the power of 3" is 6×6×6 and 6 "raised to the power of 4" is 6×6×6×6. There are 2 ways of looking at this:
|
|
|
In this particular case 6 raised to the power of 4 tells us that we have 4 instances of the number of 6 all of which are multiplied together, so we could expand this to include a variable "n" and "n" instances of any particular number to show that number raised to the "nth" power. |
|
|
|
|
|
In this particular representation, which is the less frequently used. The number is multiplied by itself the same number of times less one as the power, so in the example above, 6 "raised to the power of " is actually the number 6 multiplied by itself (4-1) times. |
|
|
Let us now take a look at some numbers:
From the examples above hopefully you can see now that 6 "to the power of 1" would be just "6 because in either representation (left) the power gives us the first and only instance of the number 6, and (right) n-1=0 so this tells us that the 6 that is there anyway, is not further multiplied because n-1=0. Either way, 6 raised to the power of 1 is 6
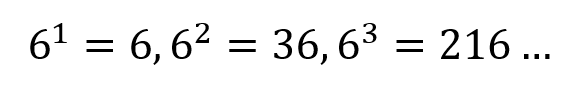
Let's now go the other way, let's start looking at some fractions involving 6. First of all let's take a look at the simplest example, "one sixth" or 1/6.
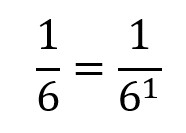
This expression is correct because if you look back over the last few lines, I have shown you that 6 raised to the power of 1 is indeed 6. 6 raised the power of 2 is 36 and so on. So is there a way that we can represent the fraction "one sixth" as an index? Look back previously we said that one divided by 1000 was 1/103 and we ultimately called that 10 "to the power of -3". Can we do the same for other numbers?
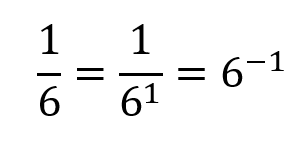
This is correct, if you put 1/6 into a calculator, you will come back with 0.166666 recurring, similarly if you enter the expression "6 raised to the power of -1" into your calculator you will arrive at the same recurring decimal number, this proves that one divided by 6 to the power of +1 is the same as 6 raised to the power of -1. This works for any number. So, why am I actually telling you this? Let us generalise just one small and then I will explain why this is so important when it comes to units.
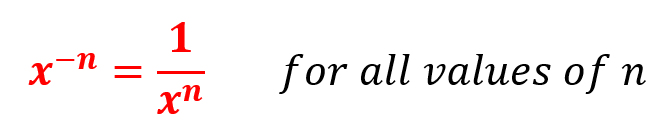
Back to >> Concentrations <<