Concentrations

We will now start looking at some calculations involving concentrations. These sorts of calculations almost always involve aqueous solutions of substances, it doesn't have to be water of course the solvent can be anything but more often than not it is water that we talk about.

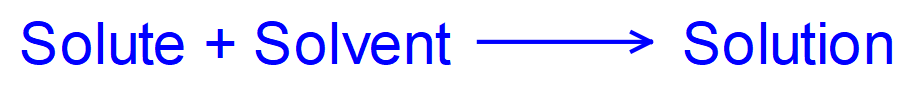
When you create solutions like this, the amount of solvent and the amount of solvent will determine the "strength" of the solution you end up with, we usually refer to this as the solutions "concentration".

There are a couple of ways of talking about concentration, we can talk about this in "molar" quantities, that is how many "moles" of a solute is dissolved in a certain quantity of solvent, or we can simply talk about the mass of the solute measured in a suitable unit (usually grams) dissolved in a given amount of solvent (usually cubic centimetres or litres/decimetres cubed). For the purposes of the earlier part of this section, we will deal with the mass and volume method first as the molar method can sometimes cause problems (students seem to find difficulty dealing with moles so I would like to spend a bit more time on this). First of all, let us look at a basic equation to give us concentration in grams per decimetre cubed. Remember that decimetre cubed and litre are used synonymously as there are 1000 cm³ in a decimetre cubed and 1000 millilitres in a litre. More often than not the solvent we are talking about will be water which has a density of approximately 1 g/cm³ hence the interchange between decimetres and litres.

There does appear to have been a swing back to using decimetres, litres and millilitres appears to be falling out of favour which could be due to the fact that not all solvents have a 1 g/cm³ or 1 g/mL density. For the rest of this topic and probably for the rest of this book I will work using decimetres cubed and centimetres cubed.

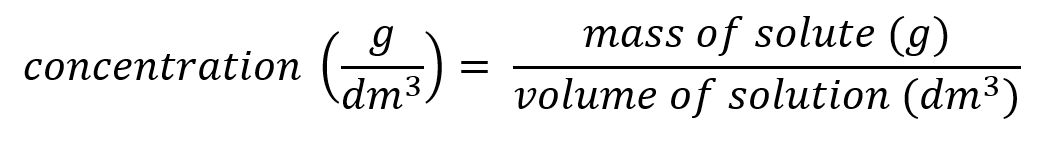
It is very important to mention something here, in fact 2 things:

It is just as important to get your units right as to get the right numerical answer, in an exam question you could lose part of a mark if you quote your units incorrectly or you fail to quote them at all.
Usually, as in the example shown you will see the units represented as "something per something" and you may see shown, as in the example as "g over decimetres cubed" :

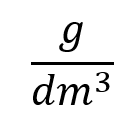
Or you may see it represented this way:

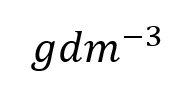
If you are intrigued as to where the second representation is derived from, have a look here in >> Appendix 1 <<

Moving back to concentrations, we said that a "certain number of grams of a solute" dissolved in a "certain number of cubic centimetres of a solvent" would give a concentration of "a certain number of grams per cubic centimetre" and this is usually represented with the mass of the solute divided by the volume of the solvent. An example could be 55g of copper sulphate dissolved in 1000 cm³ (1 cubic decimetre) of distilled water, this would give us a copper sulphate solution with a concentration of "55 g per decimetre cubed"

Now watch.......

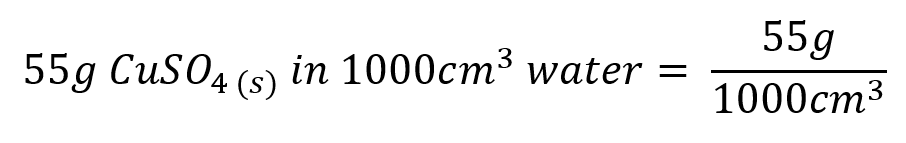
Remove the numbers from the right-hand side of this equation and just leave the units:

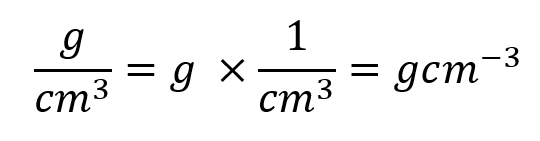
Of course we would not ordinarily say 1000 cm³, we would in fact say one decimetre cubed which is 1dm3

Q. Taking into account our solution of copper sulphate, state its concentration as shown in grams per decimetre cubed.

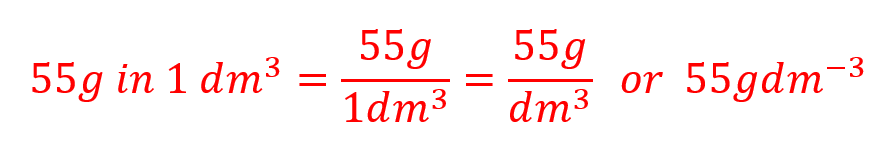
Although you might not actually realise it, you have calculated two results here, a numeric one and an alphanumeric one. To arrive at the answer at the end of the equation above you have performed these 2 calculations and put the answers together:

Q. State the concentrations of the following solutions in grams per decimetre cubed:

(a) 48 g of solid copper nitrate dissolved in 1000 cm³ of distilled water

(b) 76 g of solid potassium manganate (VII) ( potassium permanganate) dissolved in 5000 cm³ of distilled water

(a) this one is quite straightforward, we know that 1000 cm³ is 1dm3 and so we can say that the concentration of copper nitrate solution is 48 g per cubic decimetre or 48gdm-3

(b) 76 g of potassium permanganate is dissolved in 5000 cm³ of distilled water. We have to work out the fact that this is actually 5 cubic decimetres of water and so the calculation will look something like this:

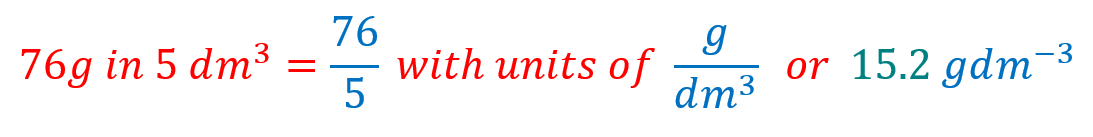
(c) 213 g of sodium chloride is dissolved in 250 cm³ of distilled water. How many decimetres cubed is 250 cm³? Well, 250 cm³ is one quarter of the cubic decimetre so we can enter these values directly into the equation even though we have a fractional denominator, as long as you enter it into the calculator properly you will get the right answer:

In the case of this last example it is probably unlikely that you would manage to dissolve that much salt into such a small amount of water, do not let this concern you because the figures have just been plucked out of the air to aid the illustration, these are not meant to be representative of actual, factual occurrences. It's just to get you used to the maths !!