Worked Examples in Science and Mathematics

Generally, in any arithmetic computation set as an examination question or homework task, the level of precision that you would be expected to quote your answer to will be governed by either the data that you are given to work with, or the required level of precision will be specified in the question.

For example, if you were asked to calculate the following:

Logically, you would respond with the number "12". The data that you have been given to work with does not contain any decimal places so it is inferred from that that the answer you are expected to produce will be quoted to a similar level of precision.

However, if you were asked to evaluate this:

Instinct would lead you to (at least) quote this to 4 decimal places (possibly higher). In this particular case the result was of course be "12.9123" although most calculators would give you a result to 8 or 10 decimal places.

Usually the question will say, quote your answer to (a given number of) decimal places, but in some cases you may be asked to quote your answer to (a given number of) significant figures. There is a difference between decimal places and significant figures, which many people routinely confuse.

Decimal places is quite straightforward, if you asked for example to quote an answer to 4 decimal places you would take a look at the 5th decimal place and decide whether or not to "round up" or "round down" depending on the value of the 5th digit:

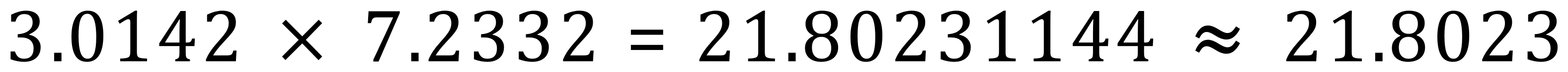
As we can see, the 5th digit after the decimal point to the right is the number 1, as this is below 5 we round down, to 21.8023.

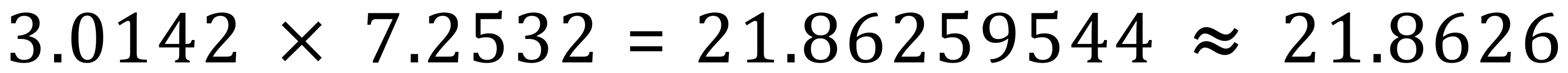
In this slightly modified example we can see that the 5th digit is now a number 9, being greater than or equal to 5 means that this time we will "round up" to give an answer of 21.8626 if quoting to 4 decimal places as before.

There is a temptation to step further back in the rounding process, this can in some cases have an effect on the end result and should not be done:

Example: State the below number to 4 decimal places:

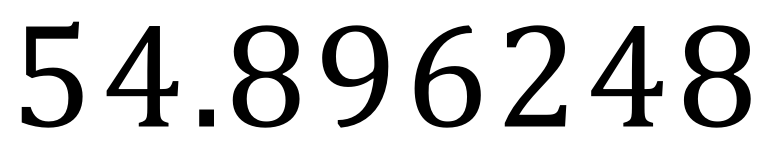
The correct answer in this case is 54.8962. Sometimes there is a misjudged temptation to round the "4" upwards to "5" because of the 8, and then to round the 4 upwards once again which would make our answer 54.8963. This is not correct.

Significant figures is slightly more complicated.

Q. Calculate the result of the following expression and quote your answer to:

• 3 decimal places
• 3 significant figures

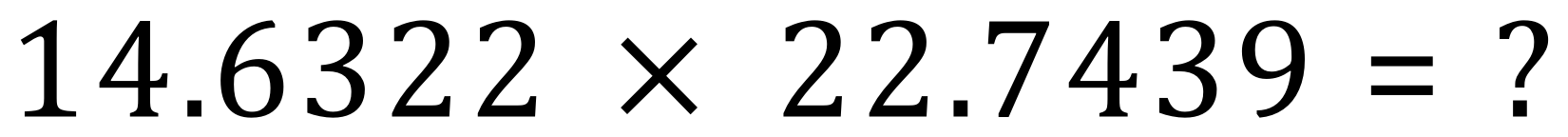
The "raw" result is:

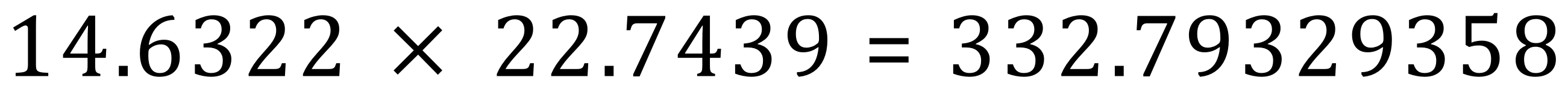
Straight off the calculator, reported back to 8 decimal places. It should be quite straightforward to see that the result to 3 decimal places would be 332.793, as the number 9 in the 4th decimal place causes us to round upwards.

However, what exactly is a "significant figure"?

Significant Figures (sometimes referred to as "sig figs") start at the first NON ZERO digit in the number concerned:

So in this case the number to 3 significant figures is 333

In the case of small decimal numbers:

In certain circumstances, in mathematics numbers will be approximated (or rounded) to make them easier to work with. This is, as the name might suggest when we need to only work with a rough value or an "approximation" of the true value. For example if I was quoted the number 5287.73 and I was asked to approximate it, then I might say 5300, 5290, 5288 and so on depending on the precision I was asked to approximate to. Speaking very widely I might even just say "about 5000" but there are certain rules which must be applied when dealing with approximations.

We can approximate:

To the nearest whole number

To the nearest ten

To the nearest hundred

To the nearest thousand

Depending on the precision required.

Examples:

Q. Round the following numbers to the nearest whole number - 9.7, 13.3, 22.9, 45.8 and 89.4

A. Remembering the basic rules of arithmetic that if a number is 5 or more it is rounded up to the next increment and if it is 4 or less it is rounded down - these numbers would then become 10, 13, 23, 46, and 89.

There are 2 other types of "rounding" that we need to consider and these sometimes become misunderstood. we can round to a certain number of "decimal places" or to a certain number of "significant figures". Any question asking you to round will tell you the number and the unit to round 2 in other words a question might end:

 ".... State your answer to 3 decimal places (usually d.p." or ".... State your answer to 2 significant figures (usually s.f. or sig fig)...." 

The first of these, rounding to decimal places Is probably the most straightforward one to understand, so we will deal with that one first.

Let us take the (soon to be in any case hopefully) well-known mathematical number "pi" which is an irrational number (that means that the decimal part goes on infinitely" but many people know it as 3.142. To 8 decimal places pi can be quoted as 3.14159265 but how would be round this? Many students make the mistake of rounding all of the decimal places from right to left, so they would look at 5, make the 6 into a 7 make the 2 into a 3 leave the 9 as it is because 3 is less than 5 and so on and so on but this is not necessary. To round a number such as this to, say 3 decimal places you would look at the 4th decimal place and decide which way to move, you do not need to look any further. So in this case 3.1415 would be rounded up to 3.142, you do not need to look at the 9 and round the 5 up to 6, the reason for this is that sometimes you may have a decimal ending with a 4, followed by number greater than 5. The temptation would be to therefore round of the 4 to 5 and because it is now 5 or above to round up once more, this would be incorrect.

Q. Round the following numbers to 1 decimal place, 2 decimal places and finally 3 decimal places - 16.38264 249.73042, 77.16985, 103.28444, 87.9648

A. Let's put these into a table just to make it a little bit clearer:

If you study these numbers you should be able to see how the roundings have been arrived at. Simply if you are asked to round to the "nth" decimal place, look at the (n +1) decimal place and decide whether to round up or down depending on whether that number is 5 or above, or 4 or below.

Rounding to a certain number of "significant figures" is a little bit more complicated. The reason for this is we have to decide which figures are "significant" and which ones are not. Mathematically the first "significant figure" is the first nonzero digit.

>> Questions <<