Highest Common Factor and Least (Lowest) Common Multiple
Highest common factor and least common multiple seems to cause a lot of problems in GCSE mathematics. But the principles are not really that difficult. We will take a look at LCM and HCF by exploring many examples to make sure that this does not cause you any problems.
Definitions - the Least (Lowest) Common Multiple (LCM) of a set of numbers is the smallest of the common multiples
Definitions - the Highest Common Factor (HCF) of a set of numbers is the largest of their common factors
There are a couple of ways to do these, we can write out the common factors and analyse the results but an easier way is to use prime factors and then insert these into a Venn diagram. This doesn't sound easy I agree, but it will show its simplicity once you have done a few.
Let's take a look at one example which will involve both a Highest Common Factor and a Lowest Common Multiple so it will be (no pun intended) common to both of these topics.
Q. Find the Highest Common Factor and Lowest Common Multiple of 60 and 72.
A. For this example only I will show the "prime factor trees" and the Venn diagram.
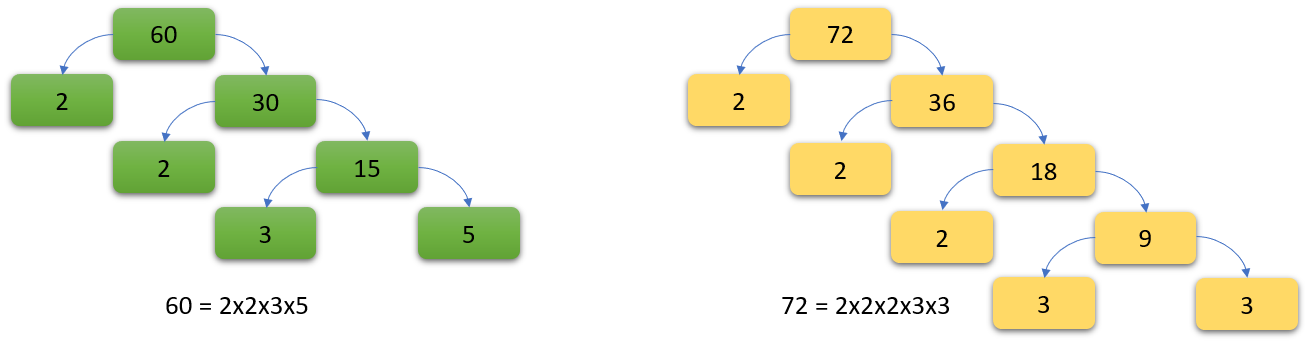
Looking at the number 60, our left-hand set of boxes shaded green shows us that the prime factors of 60 are 2, 2, 3 and 5. If we multiply 2, 2, 3 and 5 we get 60. Similarly if we take a look at 72, our number on the right in the orange shaded boxes, we can see that the prime factors here are 2, 2, 2, 3 and 3. Once again if we multiply 2, 2, 2, 3 and 3 we arrive back at 72.
Now we have our prime factors, we can construct our Venn diagram and in it we can place the values according to whether they are in common or otherwise (that is whether they lie in the intersection of the circles or not).
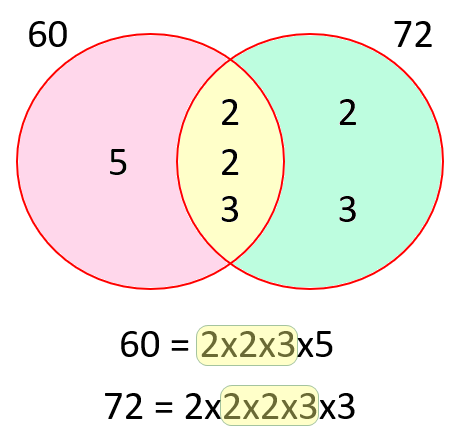
The factors common to both numbers are 2, 2 and 3 and so these numbers are entered into the overlap area shown in yellow. 5 is a factor of 60 only so it lies in the pink zone, and 2 and 3 are the remaining factors of 72 so these go into the green zone.
The highest common factor (HCF) is the product of all the numbers in the common zone (yellow), so that is, factor between 60 and 72 is 12 (2×2×3).
The lowest common multiple (LCM) is the product of all of the prime factors of 60 and 72, which is the product of all of the numbers shown in all 3 coloured sections of the Venn diagram, in other words 2×2×2×3×3×5= 360.
Let us take a look at another example, this time I won't show the prime factor trees, I will simply give you the prime factors (if you want to check them later you can) and put them into a Venn diagram as in the first example.
Q. Find the HCF and LCM of the numbers 10 and 14.
A. 10 = 2 x 5, 14 = 2 x 7

This is a very simple example, probably simpler than you would expect in an exam. We can see very quickly that the prime factors of 10 of 2 and 5 and that the prime factors of 14 or 2 and 7. The prime factor in common is to which will then be placed in the intersection of the Venn circles, and the remaining prime factors common to their respective numbers are placed as shown.
We can see straight away therefore that the highest common factor of 10 and 14 is 2, and that the lowest common multiple is 5×2×7 = 70.
In this final example we will introduce a third circle in the Venn diagram as we are going to look at the prime factors of 3 numbers. This works no differently to the previous example, but takes a little bit more care in the placing of the appropriate factors in the intersections.
Q. Find the HCF and LCM of the numbers 9, 12 and 15.
A. Once again I will give you the prime factors which you can check at your convenience, and I will now show you these prime factors entered into the appropriate places in the Venn diagram.
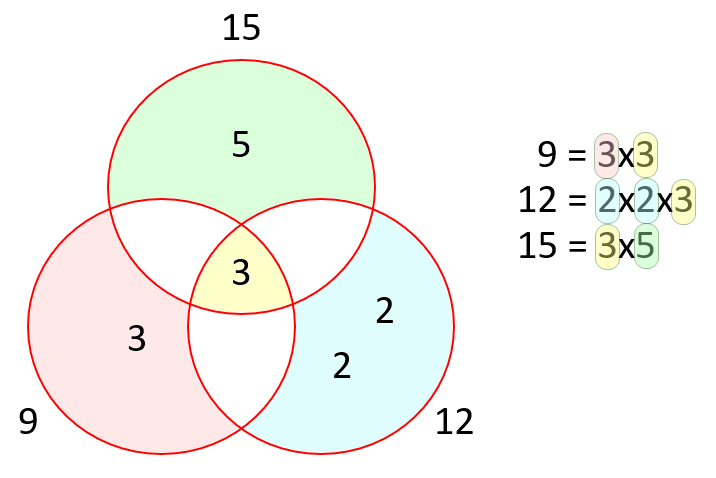
You can see from the Venn diagram that the highest common factor of the 3 numbers 9, 12 and 15 lies at the intersection of all 3 circles, shaded yellow. The HCF is 3.
The lowest common multiple of the numbers 9, 12 and 15 is the product of all of the numbers shown inside the circles, that is 2×2×3×3×5= 180.
>> Questions <<