Expressions in Science
We saw previously the below expression:
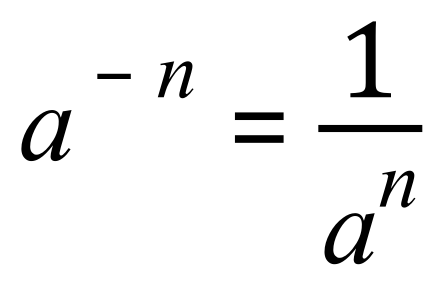
Which, if you study it, will tell you that a number raised to a negative index is the same as "one over" the same number raised to the equivalent positive index. If we take a look at this using numbers instead of algebraic expressions, it may become a little bit clearer.
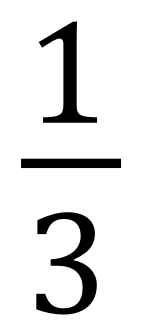
Nothing complicated about this, this simple fraction "one third" which is "1" divided by "3". If you cast your mind back to index powers, you will probably straightaway be familiar with "squared" and "cubed" because these seem to be the ones that stick most readily. But what about the number raised to the power of one? What exactly is a number raised to the power of one?
The simple answer is that any number raised to the power of 1 is the number itself, so "2 to the power of one" is 2, "58 to the power of one is 58" and "26,000,003 raised to the power of one is 26,000,003"
If we raise a number to the power of 0, the result in all cases is simply 1. Try some numbers into your calculator to see that this is in fact the case.
So, returning to our trusty old fraction "one third" it is in fact "1 raised to the power of one divided by 3 raised to the power of one!", and if we take it a little bit further and refer back to our original diagram we would be safe to say that this in turn would be "3 raised to the power of -1". Again, put some of these expressions into your calculator and you will indeed see that "3 raised the power of -1" comes out at 1/3.
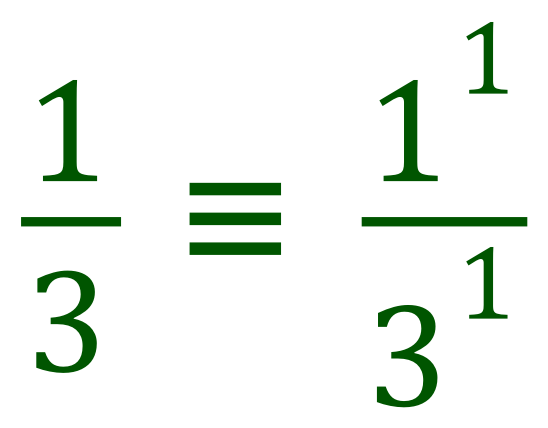
Now let us turn our attention to some of the more familiar units that we might encounter in science. Let's look at the standard unit for velocity, which is "metres per second":
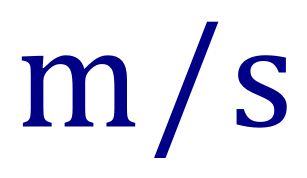
The "/" is an abbreviation for "per" so if we were to have a velocity of X metres per second, we would write it this way:
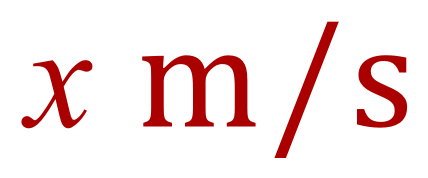
We would have course interpret this as an object moving at "x metres" in "1 second". To calculate velocity we divide distance by time, so an object which moves, for example 5 m in 5 seconds will be travelling at 1 m/s.
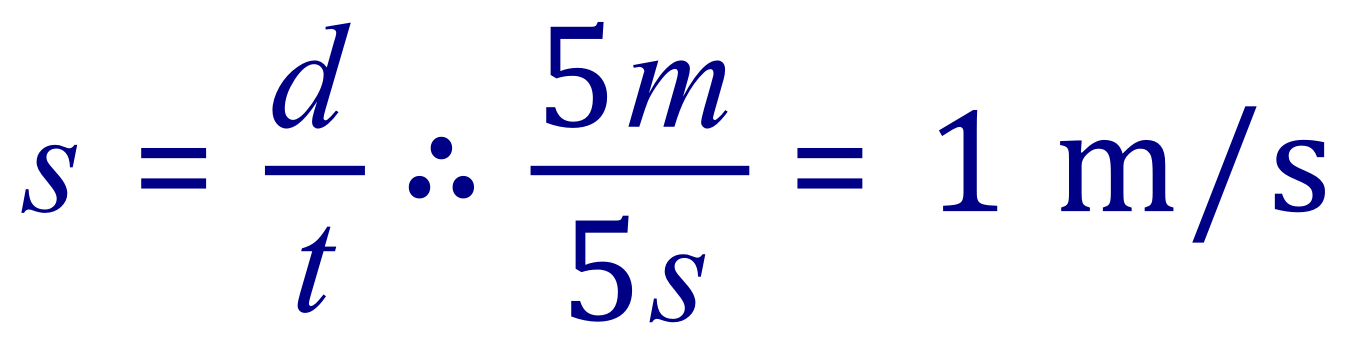
In the equation, and that part of the expression immediately before the second equality, we see our information be represented in what appears to be a fraction type format, however, our answer appears to have been quoted in the familiar "metres per second" format where "per" once again is the "/".
We can of course write it as a fraction if we wish, and could express a units as "m over s":
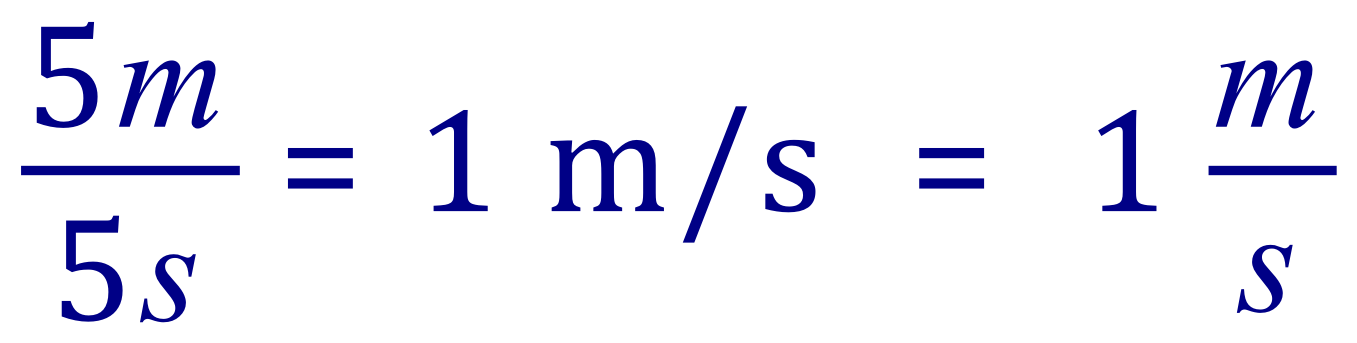
You've probably got so used to seeing this in the first format (using "per") that the second format looks a little bit alien, however it does lead me nicely into the purpose of this particular section.
One number divided by another number can equally be displayed as the product of the first number and the reciprocal of the second. To try to demystify this let's take a look at an example.
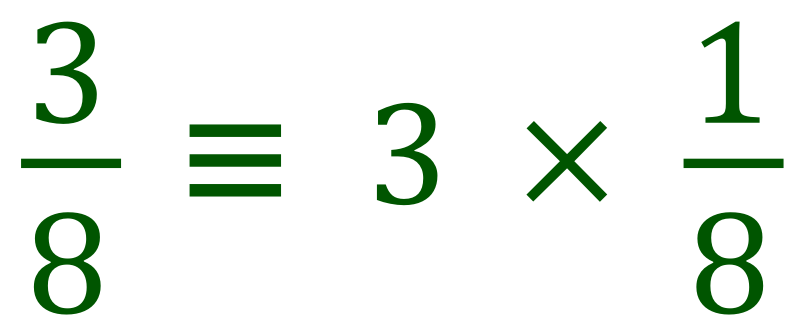
Now we already know, that our fraction "1/8" can be written as "1 over 8 to the power of 1" which is the same as "8 to the power of -1", so our expression above could be extended:
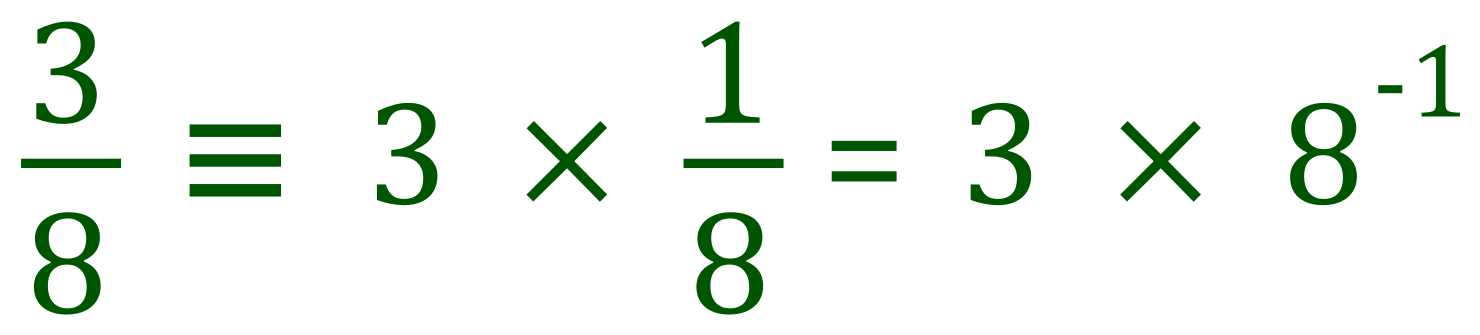
Now let us go back to our units, and in particular the example of velocity that we were looking at before:
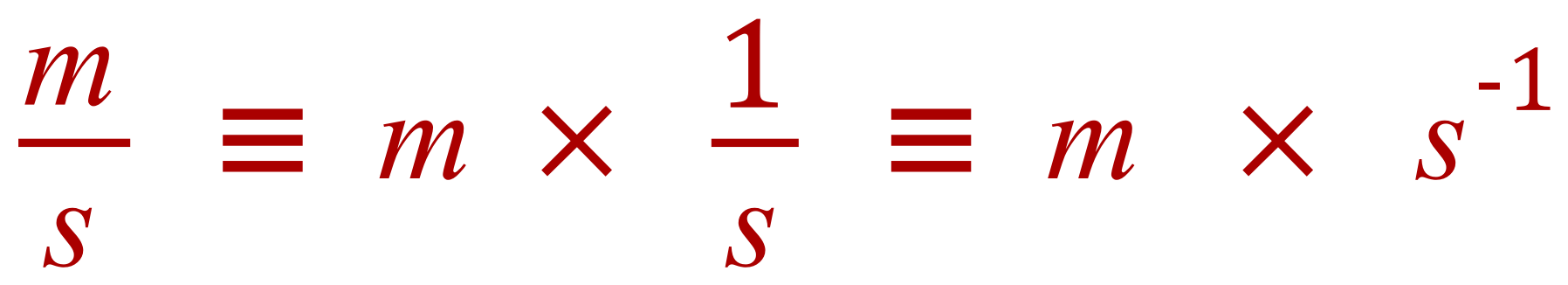
This is how you will sometimes see units represented in science, the usage of "raised to a negative power" seems to come in quite a lot at advanced level and beyond, for example if we consider the concentration of a substance in "moles per litre" you shouldn't be surprised if you see it written this way:

Although at GCSE level the "per" method seems to be favoured.