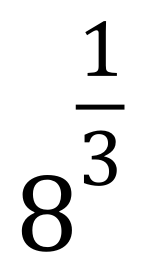Powers Indices and Standard Form
When we look at a number, we are actually looking at more than just a number, it is an entity representing a value which occupies a place on the number line.
The picture above, depicts a small section of the natural number line. The origin is set at zero with all natural positive numbers to the right and all natural negative numbers to the left.
To the right of number one we have number two and to the right of number two we have number three and so on, similarly to the left of -1 we have -2 and to the left of -2 we have -3 and so on.
From the point of origin, set at zero, the number line extends to the right and to the left infinitely and between each number we have an infinite number of fractional/decimal values so that for example exactly midway between zero and one we have the fraction ½ or the decimal value 0.5
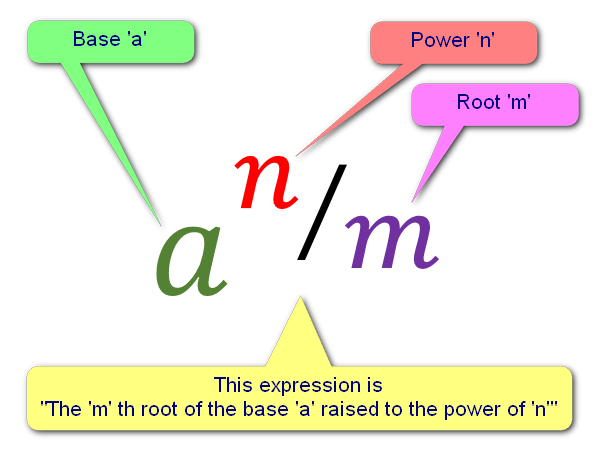
So, what do we mean by Powers? - It would probably be useful at this point to bring in the correct terminology, “Exponentiation” which is defined as being a mathematical operation involving two components:

What we have here, is a number ‘a’ “raised to the power of ‘n’”
Let us take a look at an example:
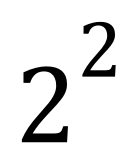
In this particular case our base and the exponent have the same value, that is the value 2 but the subtle difference is that the larger 2 is the base which is being raised to the power of the exponent so effectively they have different jobs.
In this particular instance 2 raised to the power of 2 is 2×2 which is of course 4.
What about this……
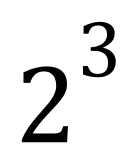
Well, if I was to say that this is 2 x 2 x 2 = 8 can you see a pattern forming already?
OK……formally we can say that:
“A number raised to a positive power (exponent) is that number multiplied by itself as many times (less 1) as the exponent value”
So 23 is in fact 2 multiplied by itself a further 3 - 1 = 2 times.

Right, you have to be aware that if you are told that 23 is 2 multiplied by itself 3 times this isn’t correct, because that would be 2 x 2 x 2 x 2 = 16.
Accepted practice is to exclude the first instance of the base and to say that:

The general rule for positive powers:
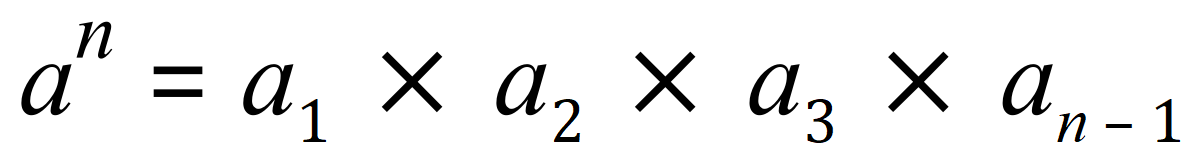
There are a few special cases to remember:
a2 is also referred to as ‘Ay Squared’, similarly a3 is referred to as ‘Ay Cubed’ but from then on we usually say that an is “Ay to the Enth” or just “Ay to the Enn”
What happens if the exponent is 1 or 0? – Perhaps we should talk about these cases before we go further back in the number line (into the negative numbers).
OK…….think about the general rule, an = ‘a’ times ‘a’ up to n-1 times, well in this case we have n=1 so n-1 is zero, in other words we don’t multiply ‘a’ by itself at all (well, we do….but its zero times) so effectively ‘a’ stay as it is:
General rule:
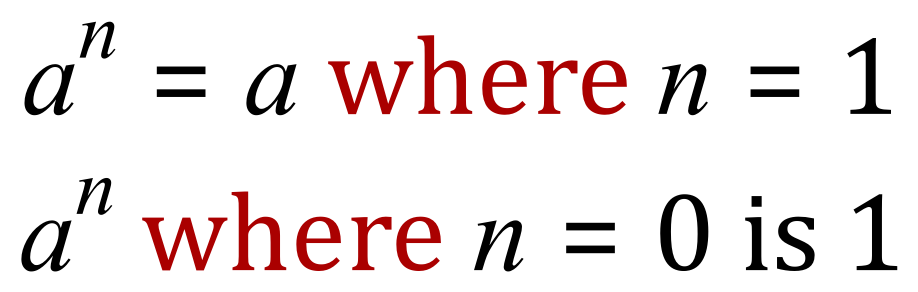
ANY number raised to the zero power is 1.
So now that we have established this, what happens when the number ‘n’ is negative? For example what if n was ‘minus one’?

Well, the rule here is that any number ‘a’ raised to a negative power ‘-n’ is the same as the reciprocal of ‘a’ raised to the positive equivalent of ‘n’:
So:
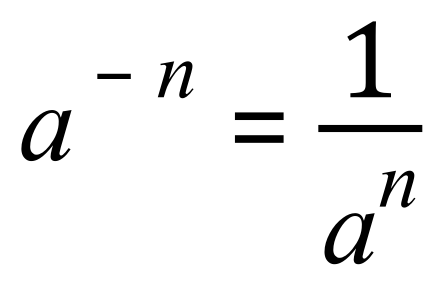
This is quite straightforward, we have looked at positive integer powers and negative integer powers:

But what about if the value for ‘n’ is not a whole number, for example what would you make of this:
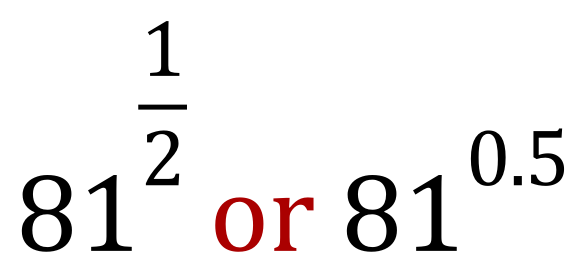
This needs some explanation, in both cases the answer is 9 but how do we get that? Powers and indices involving fractional or decimal values are taking us into the realm of ‘roots’, that is…..square roots, cube roots etc. You are no doubt familiar with this expression:

Both of which are the same, and the answer of course is 5.
In the second example the power is given, usually if we are talking about the ‘square root’ of a number then the small index is omitted as it is implied to be a square root, but any other root must have its power / index shown.
So…what is the answer here?
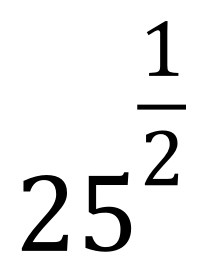
The answer is again 5, because raising a number to the power of a half is the same as taking the square root. So now if we go back to the top of the page we can see that the value of 81 raised to a half (or 0.5) is indeed 9…the square root of 81.
Before we come to a generalised rule, let’s look at a few more:
|
|
This is the cube root of 8, or 2 |
|
|
This is the sixth root of 64, or 2 |
|
|
Tricky one, first of all convert the decimal number to its fraction which is one quarter. Then you will see that the question is asking for the fourth root of 256 which is 4 |
Ouch……this is getting tricky, eh? What happens if my fraction doesn’t have a numerator of 1? for example what is the result here?

OK we can turn the decimal component into a fraction:
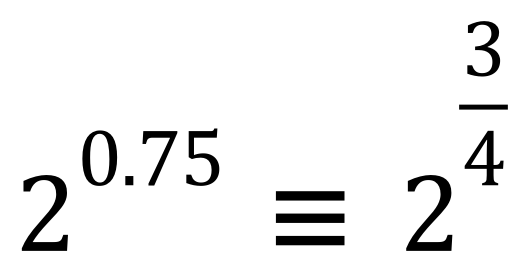
This looks a bit familiar, it’s a ‘fourth power’ because there’s a ‘4’ in the bottom, but it can’t be the fourth root of 2 because that would be 2 raised to 1/4. Well….what we have here is a ‘fourth root of a number raised to the third power’, so to work this out we first need to ‘cube’ 2 and then take the fourth root of the result:
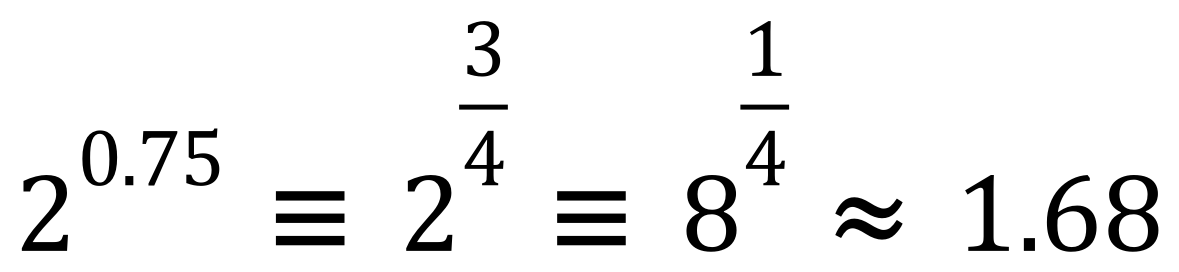
In the same way, we can see that:
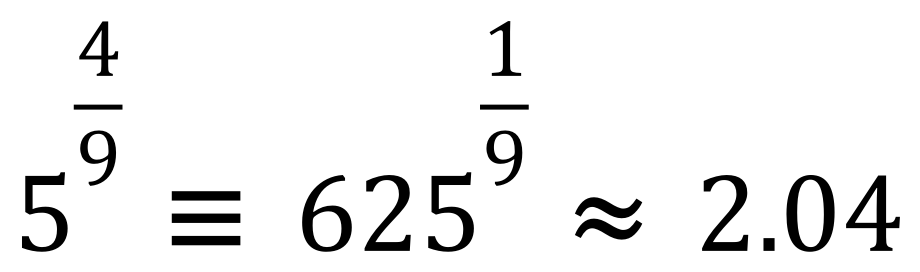
OK let’s return to our “starter for ten” ……
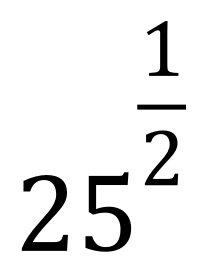
We know that it’s the square root of 25 which is 5, but now that we have explored powers and indices a bit more we can restate this by saying that:
25 raised to the power of a half is the same as the square root of 25 raised to the power of one
(because any number raised to the power of 1 remains unaltered)
One more……
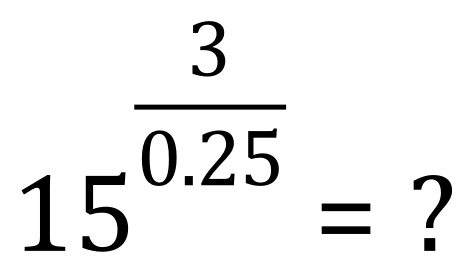
(The answer is 129,746,337,890,625 but can you see how I got there?)
General Rule: