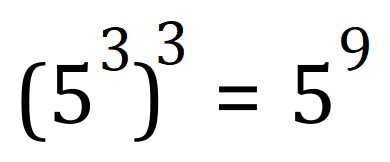Worked Examples in Science and Mathematics

What about multiplication and division of numbers in ‘index’ form? Take a look at this expression:

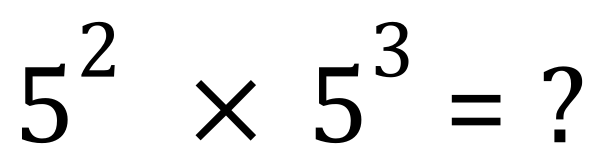
We can of course ‘do the maths’ and work this out as 25 times 125 = 3125, but also take a look at this expression:

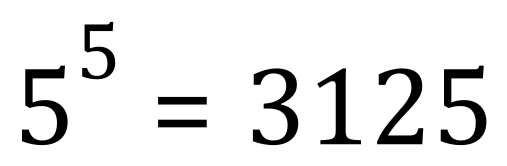
Study them both for a moment, can you see any similarity, or anything that makes it a bit more obvious that the expressions are the same? If I combine the expressions it might be a bit clearer:

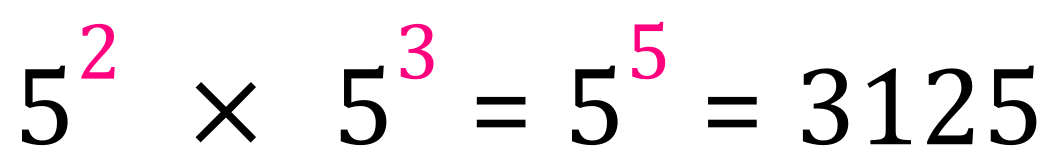
Got it?..............OK, to multiply powers of numbers, we ADD the index values together. 

Take a look at these examples:

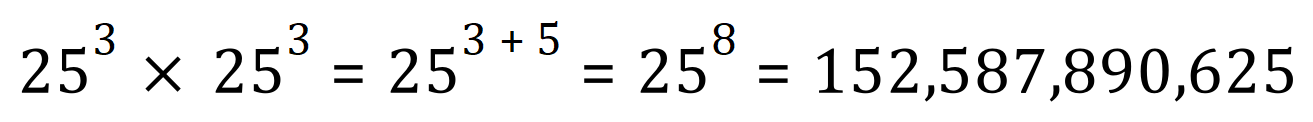
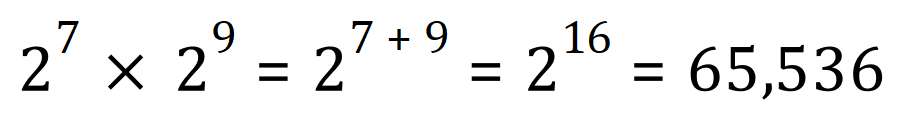
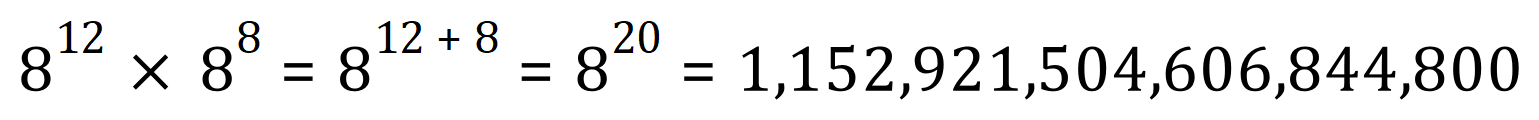
In each of the three cases the ‘base’ has been the same, and the calculation has just been a matter of adding up the index values.

Don’t worry if you end up with a negative index, look back in this document to see how to deal with those:

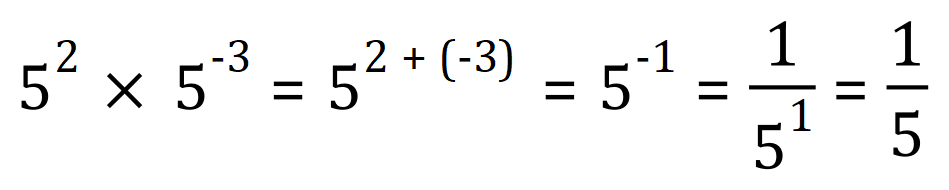
Because 2 + (-3) = -1

Similarly:

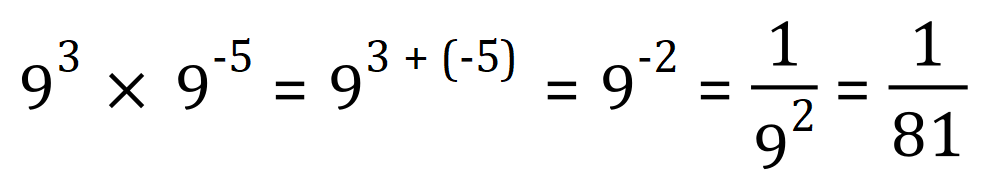
Because 3 + (-5) = -2

OK, have a think about this….

Q. If multiplication of numbers in index notation involves ADDING the index values, what do we do with division of numbers in index notation?

A. SUBTRACTION!

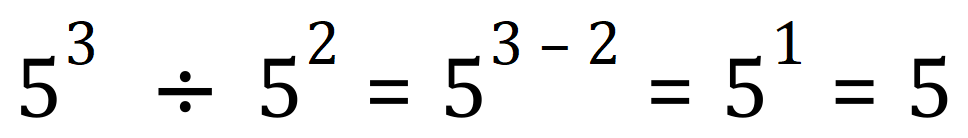
General Rules:

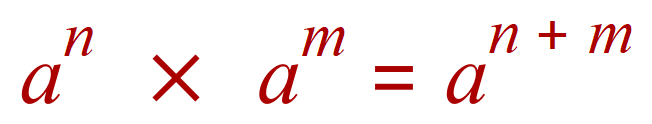
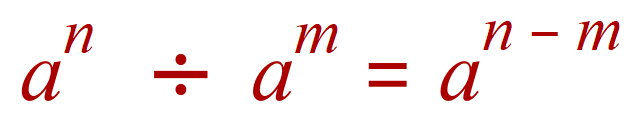
So far, we have talked about powers and indices, but we have only considered multiplication and division…..what about ‘powers of powers?’

Look at this:

This can’t be just a case of adding the index values, substitute a value for ‘a’ and see for yourself:

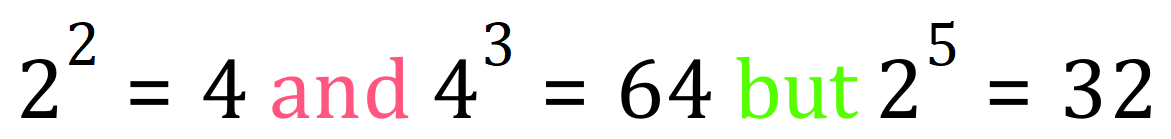
Note though, that if 2^5=32 then it follows that 2^6=64 so what is the link between the index values of 2, 3 and 6?

You might have spotted that 6 is the product of 2 and 3, so when we ‘raise a power to a power’ we actually multiply the powers together:

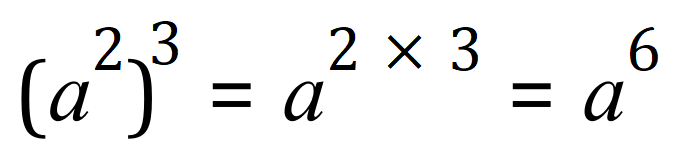
General Rule:

Try these on your calculator to prove it: