Simplifying Expressions 1
In the next section "Simplifying Expressions 2" we will meet expressions such as this one:
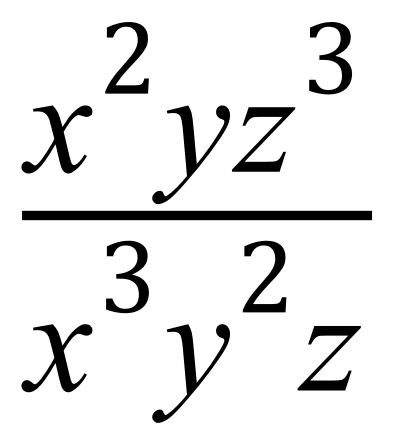
Quite a nasty looking beast but really easy to work with when you know the rules. This section will look at how we arrive at expressions like the two above which are (in this case) put together as a fraction.
Let's start at the beginning, consider the simple algebraic expression:
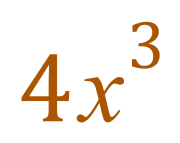
As you probably know, if we expand this, we can show where it came from in terms of numbers and variables:
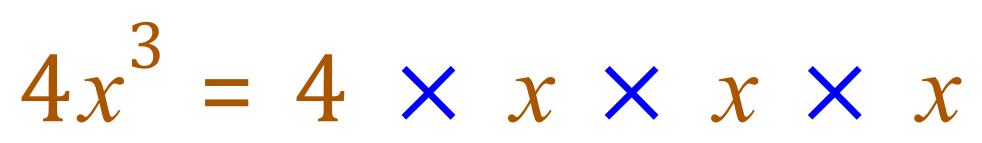
Or in words ..... "four times "x" times "x" times "x" = four "x" cubed". Remember, "x" is a VARIABLE and can have ANY value, for example if we were to let "x = 3" then our expression would become:

Just a simple reminder for powers:
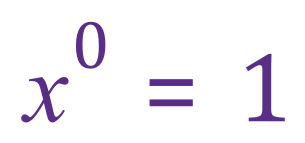
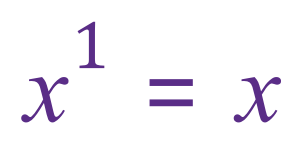

Remember : ANY number raised to the power of 0 is ALWAYS 1
OK, now its time to look at some examples and set a few rules to follow. If you work on the rules in the order given, and think carefully, you will have an easy time with these expressions:
Example: Simplify this expression:

Remember from your knowledge of index powers that when we MULTIPLY two "like" variables we ADD the powers, so:
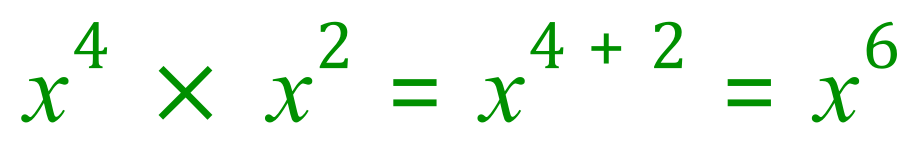
Prove this to yourself by giving "x" a fixed value, say "x = 2", we will then have:

Example: Simplify the expression:
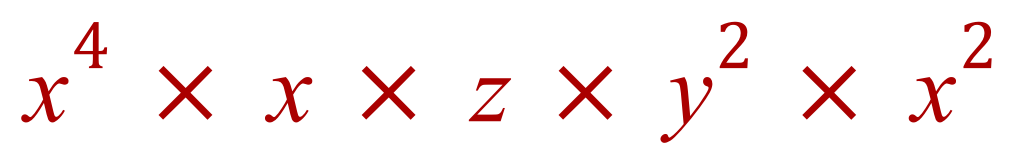
There are some steps to take here, DON'T be tempted to start adding powers up, it doesn't quite work that way.
Step 1 - collect "like" terms (as we have done before) and rewrite the problem. It will help if you do this in ALPHABETICAL ORDER:
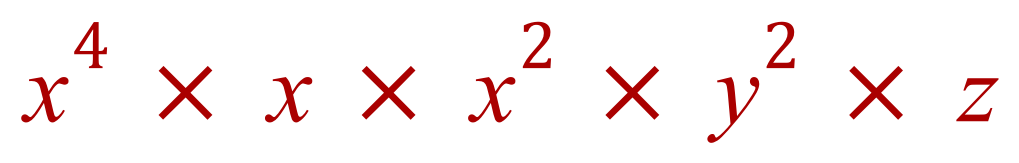
Step 2 - merge together your "like" terms using your knowledge of index powers, in this case we only have to do this for "x"

Step 3 - put together the remaining variables, leave out the "multiplication symbol" because as you know we don't usually show this:

This is the final answer. If you want to put some numbers in to prove the result, you can.
Let us call x=1, y=2 and z=3:
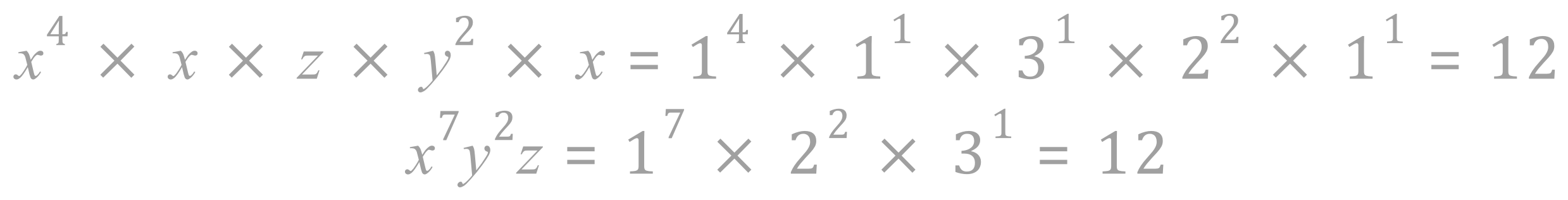
INTEGERS
Sometimes there might be an "integer coefficient of a variable" which is just a maths teacher's way of saying that there might be a number in front of one or more of the variables. So, what do we do with these?:
Well, integers are not variables, they have fixed values and so we can multiply them together to come up with a fixed result:
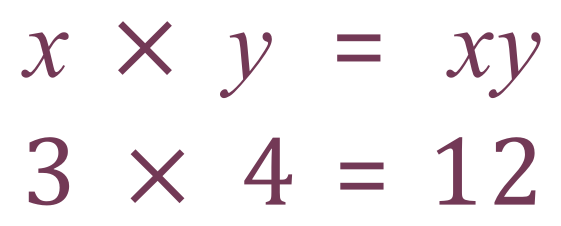
In cases where we have integers, we will still work on our "like" terms as we did before but we will multiply out the integers along the way:
Let's have a look at one:
Example: Simplify the expression:

Step 1 - Collect "like" terms and rewrite (restate) the problem:

Step 2 - Use index rules and multiplication of coefficients to "group" expressions:
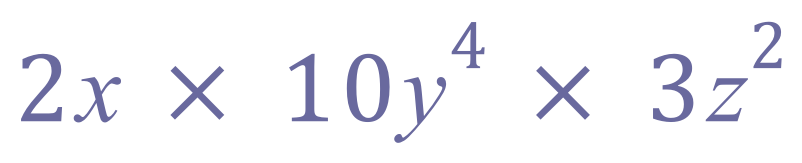
Step 3 - Assemble the result, remove operators (multiplication signs), don't forget to multiply the integers:
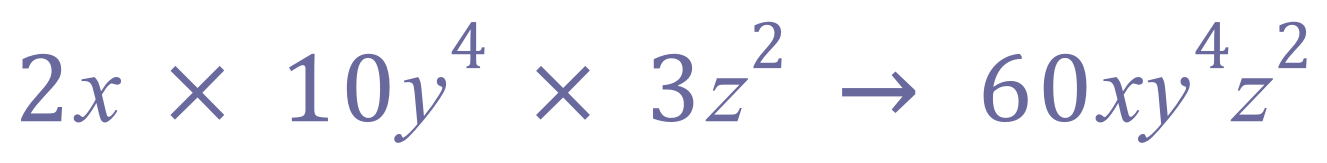
Step 4 - (if you wish, this is optional) - prove with some numbers:
Let x = 2, y = 3 and z = 4
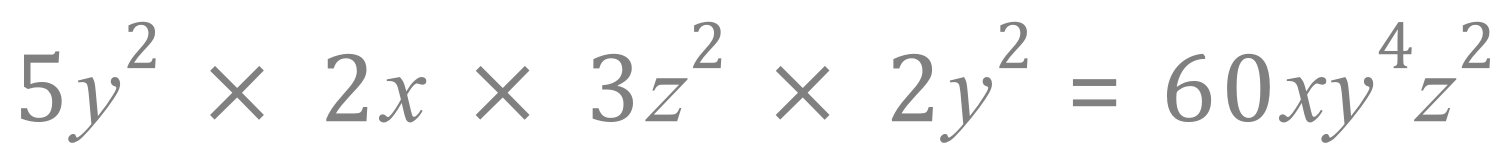

So the steps are:
Step 1 - Collect "like" terms and rewrite the problem alphabetically.
Step 2 - Use index power notation to "merge" them, multiplying out any integers in the
resulting expressions.
(repeat steps 1,2 for each variable as necessary)
Step 3 - Assemble the resulting expressions and remove multiplication signs
remember to use further integer multiplication if necessary.
Example: Simplify the expression:

Step 1:

Step 2:
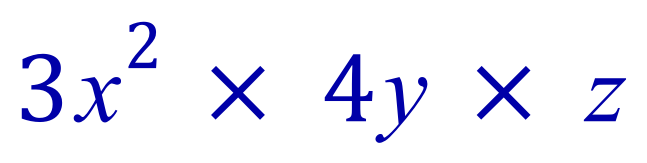
Step 3:
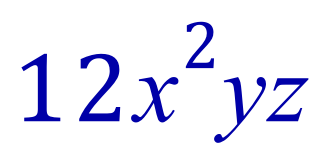
>> Questions <<