Simplifying Expressions 2
Sometimes we will do a calculation, or be given a problem where the answer can be made even simpler, so that when we state our answer (usually the last thing we write at the end of a problem) it is in its simplest form.
For example, you wouldn’t leave an answer to a question on fractions as:
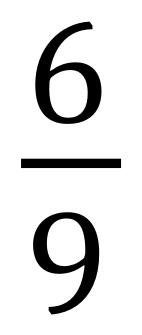
You can see that there are numbers which will divide into both number 6 and number 9, apart from number 1 we can divide number 6 and number 9 by number 3. This will “reduce” or “simplify” the fraction to this:
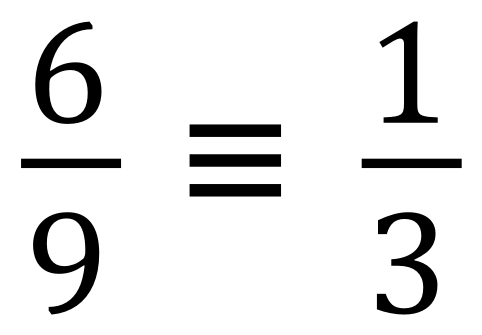
The strange looking “=” with 3 bars means “the same as” or “equivalent to”. Of course the fraction can’t be made any simpler, it is be “reduced” as much as it can.
It gets a little bit harder when we start looking at algebra, because we also have to have some knowledge of index powers:
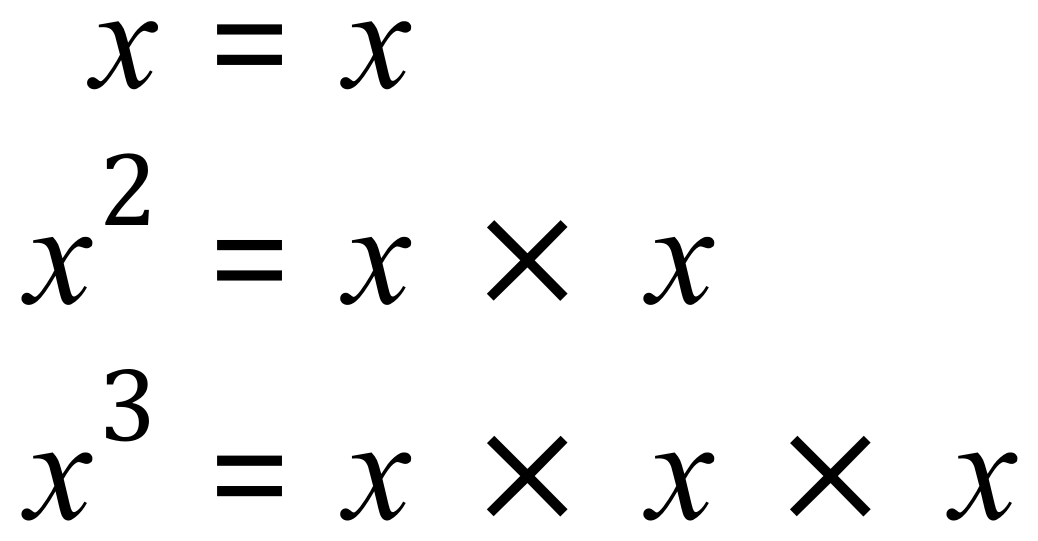
You have met these before, the index power (that’s the number) tells you how many times “x” has been multiplied by itself, less one. The very first “x” is in fact “x” to the power of one, but we don’t show the one.
The index number is quite useful, especially in algebra, and a good understanding of index notation will help you quite a lot when you start trying to simplify expressions. Before we talk about index powers, we will take a look at an expression which needs to be simplified:
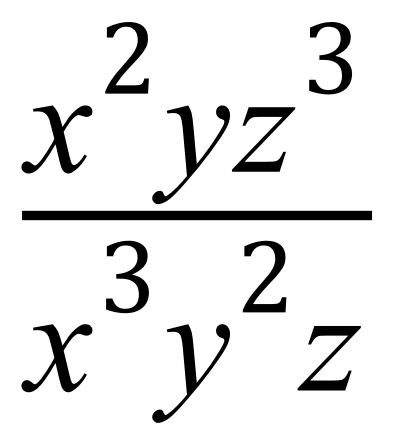
this could be the result of a problem in algebra, but because we have “x” “y” and “z” terms above and below the bar, we know that we can make this look simpler. 1st of all what exactly does the expression tell us?
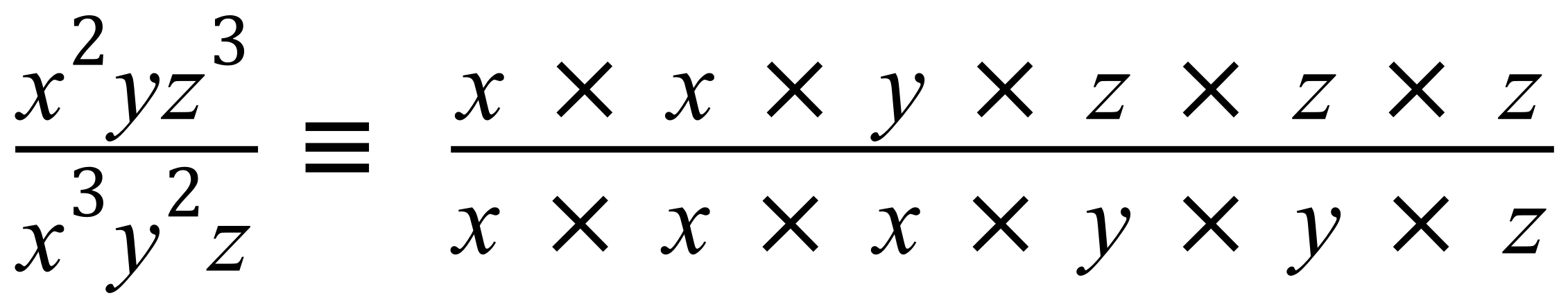
Expanding expression like this shows us that we have got 2 “x” at the top, and 3 at the bottom, 1 “y” at the top and 2 at the bottom, and finally 3 “z” at the top with only one at the bottom. Now if we divide a number by itself, whatever that number is, we end up with 1 as the result, so:
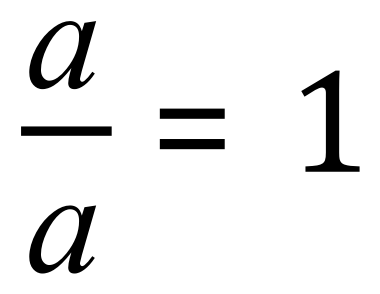
Now if we divide:
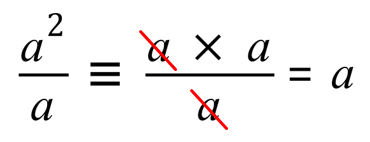
The “extra” “a” on the top cancels out with the one on the bottom, leaving us with “a” as the answer. We are going to use this idea to take a look at our first problem, to see if there is any way that we can make it simpler.

What you are doing, is taking each letter in turn and seeing if you can match the same letter top and bottom, if you can you can usually put a line through it:
- If you end up with a letter on the top without a matching letter on the bottom, you stop there.
- If you end up with a letter on the bottom without a matching letter on the top, you put a 1 the top (I’ll give you an example of this because it looks a bit confusing)
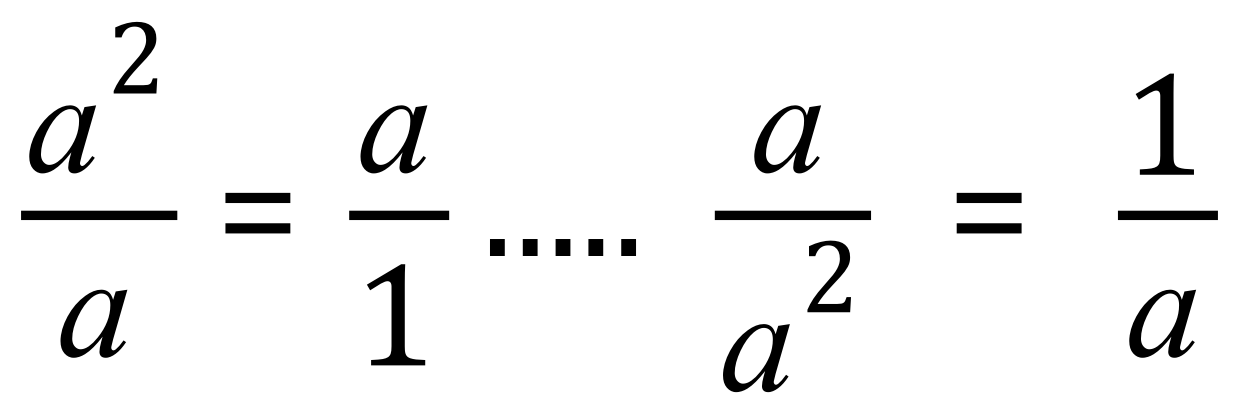
(we don’t normally show “a” over “1”, we just call it “a”)
Hopefully by now you understand a little bit more about simplifying expressions with index powers, but I’m sure you’ll agree that if we have to write out all of the expressions every time and draw a line through each matching letter is going to become very boring and tedious. Is there an easier way?, Well fortunately there is…. We work on the index number by adding and subtracting where we need to.
Let’s go back to our original expression, but this time we will just work on the numbers and you will find that it is a lot quicker.

Normally if the power is one we don’t show it, but I’ve deliberately put them in this time to make it clear what I’m going to do. First of all…..”x”
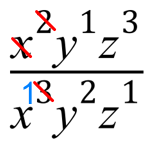
We have got 2 x’s at the top but we’ve got 3 on the bottom, so the 2 at the top will cancel with 2 of the ones on the bottom, leaving just the one on the bottom (shown in blue).
Now let us take a look at ….. “y”
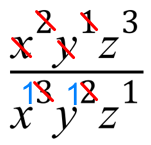
We have got 1 “y” at the top, but on the bottom, we have 2. We cancel out the one on the top with one of those on the bottom, leaving just the one on the bottom which is again shown in blue.
Finally, we take a look at ….. “z”

we started off with 3 “z” on the top and only 1 “z” on the bottom. We cancel the one on the bottom with one of the 3 on top, leaving us 2 on top which we have shown in blue.
Our final expression then becomes (once we’ve tidied up of course, and taking away any powers that are shown as 1, because if it’s a 1, as you know we don’t show it):
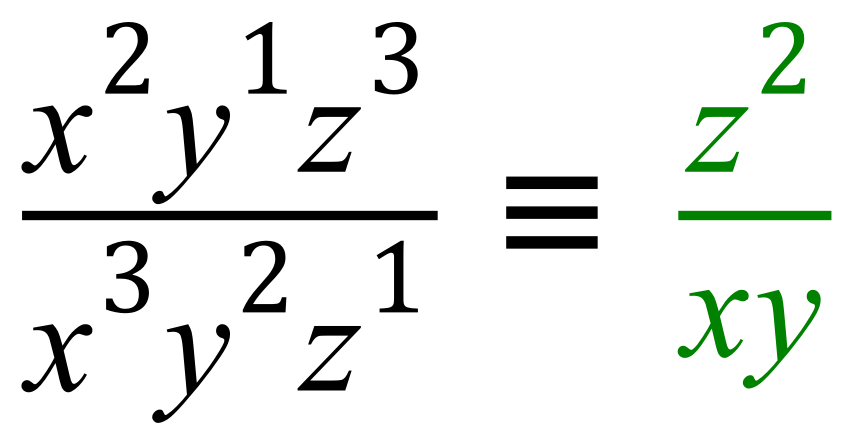
working with the index numbers is a lot simpler than having to write the whole thing out longhand, but you need to keep your wits about you especially when you have 1 as the power, remembering that it is there, but also remembering that it doesn’t need to be shown.
>> Questions <<