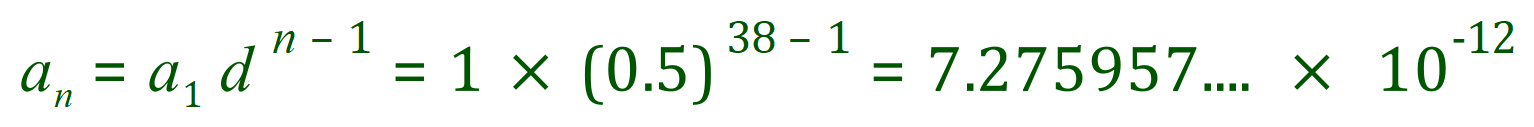Geometric Progression
We will now start to talk about another type of progression, where this time instead of adding positive or adding negative quantities we multiply or divide by the common difference ‘d’. (Note that I’ve said divide, and when we were dealing with the arithmetic progressions I referred to negatives as the ‘addition of negative’ as opposed to a straightforward simple subtraction, however when we start talking about geometric progression it may be simpler to refer to division as opposed to multiplication by a fraction, this will of course depend on the context of the question so please bear with me).
Let’s take a look at a very simple series:
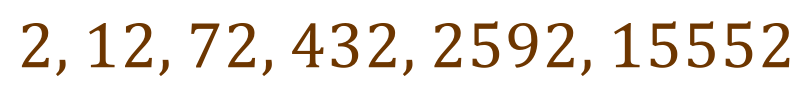
Okay, I suppose it doesn’t look that simple after all, but it is in fact a simple geometric progression where each term is obtained from the previous one by multiplication by six. Straight away you can see that we have only shown the first six terms but we are already into 5 digit numbers, so this is going to become quite big!.
If I was to say to you give me the ninety-seventh term of the series you could do it on your calculator by repetitive multiplication by six, but it’s far simpler to work out the “closed form” and plug the appropriate values into a formula.
Let’s start taking a look at how to establish such a closed form. We know that our first term is 2:
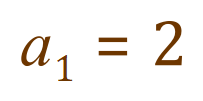
Similarly our second, third, fourth, fifth and sixth terms are as shown.
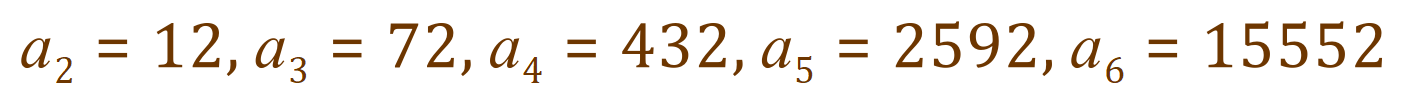
Are you with me so far?....We have been given the value for ‘d’ = 6 but it would be usual to establish this for yourself.
Now study the next term:
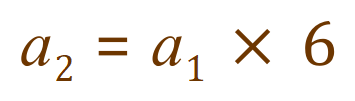
And now this one:
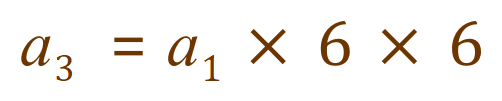
And now this one:
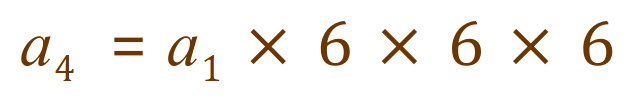
We can see that to move from one term to the immediate next we must multiply by ‘6’, or multiply the second previous by ‘6’ twice, or multiply the third previous by ‘6’ three times. Effectively we are building up our progression by saying that to get to any particular term we either multiply the immediately previous term by the common difference, or multiply the first term in the sequence by the common difference (n -1) times.
Of course, if we’re going to keep writing out “6×6×6……” It’s going to get quite laborious, so it would be simpler just to use the power notation of 6 to the power of ‘n’. Looking at the equation at the top of this page, where we are dealing with the fourth term in sequence a4 this would become:
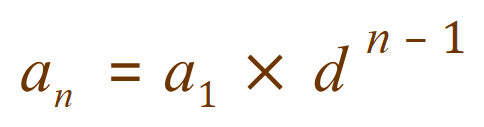
And this would be our closed form for this particular sequence. Check it out, our fourth power is 432, which is “2 multiplied by 6 to the power of 3”
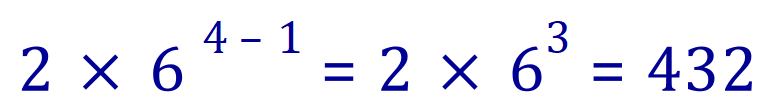
Going back to the beginning of the sequence when I mentioned finding the ninety-seventh term, we can now do this:
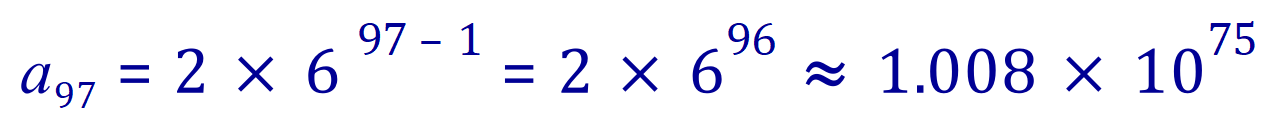
This is in fact a representation of the generic formula for a Geometric Progression:
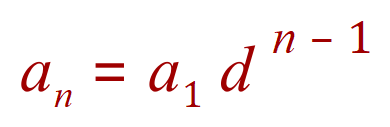
In words this means that the nth term of any geometric progression is a product of the first term multiplied by the common difference raised to the n-1 power.
Example:
Just to reinforce this a little bit more let’s take a look at another example of a geometric progression. We are given the first four terms:
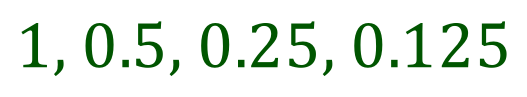
Let us take a look at the second term:
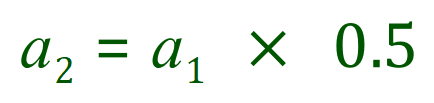
And now let us take a look at the third term:

Finally let’s take a look at the fourth term:
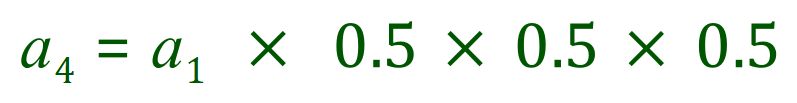
You should be able to see that to move from one term to the next we multiply the first term by the common difference (0.5) the appropriate number of times (n-1), that is:
So for example to get to our fourth term we multiply the first term by the common difference three times, to get to our fifth term we would multiply the first term by the common difference four times and so on.
Restating our equation above:
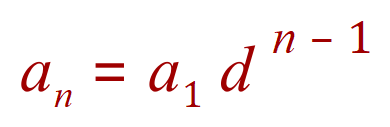
So, if by some bad luck you were faced with this question and asked to evaluate the thirty-eighth term you could do it this way: