Arithmetic Progression
Very often, in mathematics we use lists of numbers. Perhaps the most obvious list of numbers that you might come across is the ordinary integers, such as one, two, three, four… and so on. Some sequences might be obvious visually (like the red balls below) but the arithmetic nature of the "progression" might not be so clear.
Whether or not any particular list forms a sequence (either obviously, or after a little bit of investigation) remains to be seen arithmetically. Any list of numbers that relates to a situation you might find in reality will usually be finite, such as the numbers involved in the repayment of a bank loan which will probably extend for twelve, twenty-four, thirty-six or more monthly payments i.e. the list does not continue (you’re not paying the loan forever… hopefully anyway).
The first example we gave though, represents an infinite series, the positive integers starting from one and increasing by one along the number line to the right represents an infinite number of values, in “sequence” parlance each member is called a “term”.
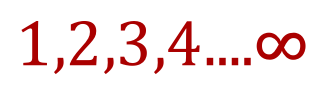
This would represent the infinite sequence of positive integers starting from one.
Most sequences have a recognisable pattern, for example if we were to consider the following sequence:
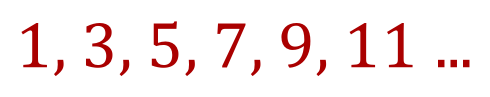
We would probably very quickly conclude that it is the sequence of odd positive integers starting from one, and that each “term” is the next positive odd integer up from the previous one, another way of looking at this is that each term is exactly “2” larger than the previous one. This is indeed a valid sequence and would go on to infinity.
In this particular document we will just look at simple sequences, which are sequences where the relationship between the terms can be identified either by inspection or by simple arithmetic. Here is a bad example:

It is in fact a series, although there is no structure to it, it is in fact the number of letters in the names of the first six months of the year but as far as sequences go it is a pretty poor example. To know what the next (and remaining) six terms of this sequence would be you have to know what it was all about, we are not always afforded that luxury which further confirms it as a very poor choice.
When we are talking about series, we represent them using algebraic letters, ‘x’, ‘y’, ‘z’ would be okay but very often and in many texts we will see the use of other letters such as ‘a’ and very often using subscripts to represent the particular index number of the term in question, for example ‘a1’ might represent the first term in the series denoted by the lowercase letter 'a'.
Let us take a look at another series, and this time we will describe it in a little bit more detail.
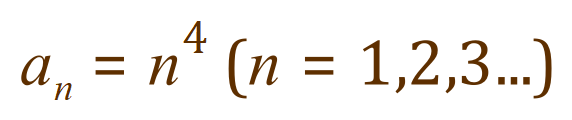
At first glance you might not really understand this, but if I show you the first five terms of the series you will quickly realise that it is in fact the sequence of the fourth powers of the positive integers from 1 to infinity, that is:

So the formula given on the previous page would be the representation of this particular sequence. The first term of the series would be a1.
Where there is a relationship between adjacent terms we refer to this as a “Recurrence Relation” so going back to a simpler series:

We can see that each term in the series is made by adding 2 to the previous term (or if you working the other way, removing 2 from it). If I were to say to you “tell me what the tenth term is?” You could probably work it out quite rapidly (the answer is in fact 19) because we are dealing with odd numbers all we have to do is double the number of the term being asked for and remove one from the result e.g. the 24th term in this particular sequence would be the number 47, but it isn’t always going to be that straightforward.
What we need is a way to work out a “formula” or “rule” (to use an older mathematical expression for formula) which will enable us to calculate any term in the sequence without having to step through each term sequentially, or resort to quite complicated memory tricks.
Such a formula, in “sequences” is called a “closed form”, or in some cases a “closed form formula” to make it a little bit more obvious that it is indeed a formula. We will soon move on to identify methods used to establish the “closed form” for the sequence and therefore be able to evaluate any term in it.
Generally an “Arithmetic Progression” or “Arithmetic Sequence” involves a series, or sequence of numbers, to which a fixed number is added (you might think to yourself “what about if we are taking away a number”, well if you think of subtraction as the addition of a negative number you are adequately covered).
Example:
So how do we actually evaluate the “closed form”? Well, let us take a look at a simple series involving the first four terms of a fairly obvious sequence:
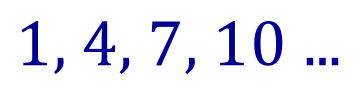
We can see that each term is made up by adding 3 to the previous term, so in our “sequence” notation we would write this as:
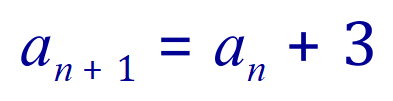
Examining the make-up of the individual terms:
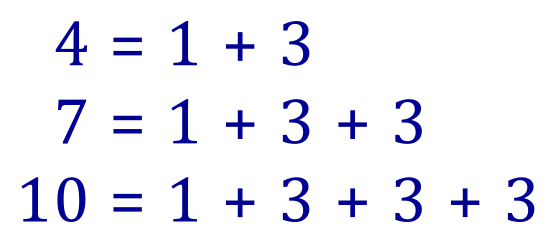
Stop and study these three expressions for a while.
To move from “1” to”4” we add three just the once.
To move from “4” to “7” we add “3” twice to “1”.
Finally to reach “10” we add “3” three times to "1".
If you study this you will see that to get to the next term in the sequence we add three just the once but if we start from the beginning of the sequence (that is with the number one) you will quickly see that we have to add three as many times as the index number in the series (that is number four lies at index 1) less one, in other words:
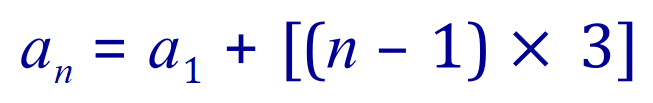
I would in fact stop at this point and study this expression quite hard. It is actually saying that the “nth” term of the progression is the sum of the first term plus the common difference (in this case three) added n-1 times.
We have to do a little bit of arithmetic/algebraic manipulation now to find our “closed form”:
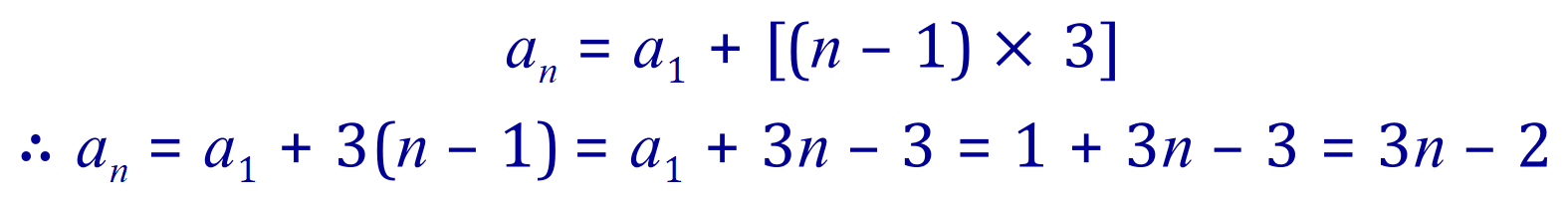
So, our “closed form” is this:
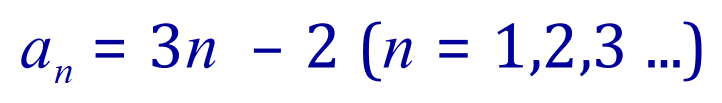
From this we can work out the value of any term in the series, for example if you wish to work out what the value of the term following 10 would be (of course we know it’s 13) but because we also know it is the 5th term therefore, n=5 we can simply substitute into the equation and indeed see that 3×5-2 is 13.
This is a very straightforward example of a closed form and will allow you to evaluate quite quickly any term in this particular progression.
Example:
Let us take a look at another example, following the same lines but a little bit more complicated because this time we have some decimal numbers. If you examine the given terms you will see that the common difference is 1.1:

I won’t write out the “gobbledygook” this time, what I will do is show you how each term is established, and hopefully you will be able to follow it:
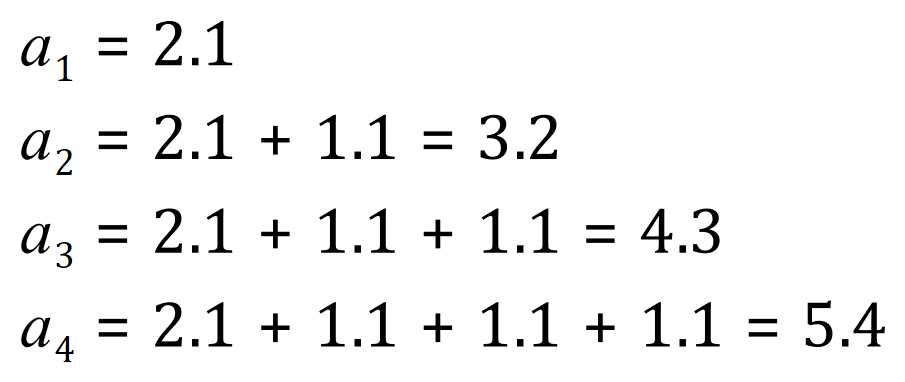
You should be able to see a pattern forming, in that the ‘nth’ term in the series is made up of the sum of the first term plus the common difference added ‘n-1’ times. If you can’t see it, study the last expression which deals with the term of the sequence where n = 4, being made up of the value of the first term (that is 2.1) plus the common difference (that is 1.1) being added n -1 (three) times:
Our closed form (first generation anyway) is therefore this:
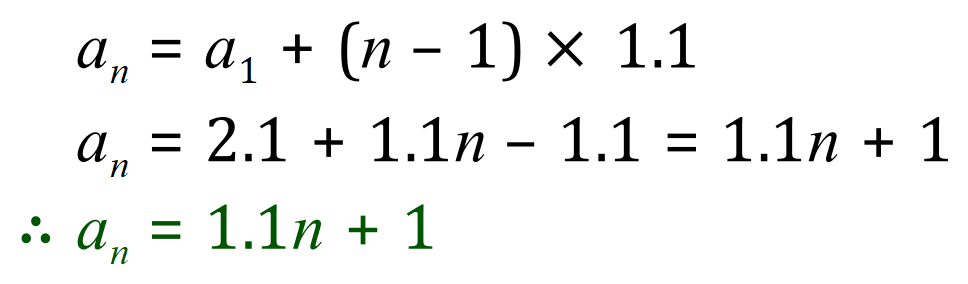
The last line is our final representation of the closed form....
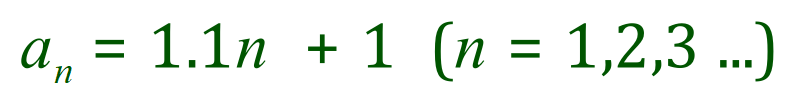
Try this out for yourself with a known value, such as n=4, we can see that 1.1n is in fact 4.4 and then when we add one to it we arrive at 5.4 which is the value of the fourth term. If we now wanted to establish, say, the hundredth term, a100, then using the closed form we could quickly establish that the value was indeed a 111.
Example:
Let’s take a look at one more example, but this time the common difference will be negative (that is it will be a subtraction although, as I said previously, we do regard this as the “addition of a negative quantity”).
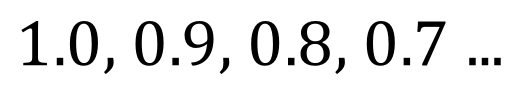
It should be quite easy to see that this is a decreasing sequence, the addition of -0.1 to each term in the sequence to produce the next one. Our first term (a1) is 1.0 and our successive terms 2,3, and 4 are as shown.
Let’s start looking at the deduction of the closed form:
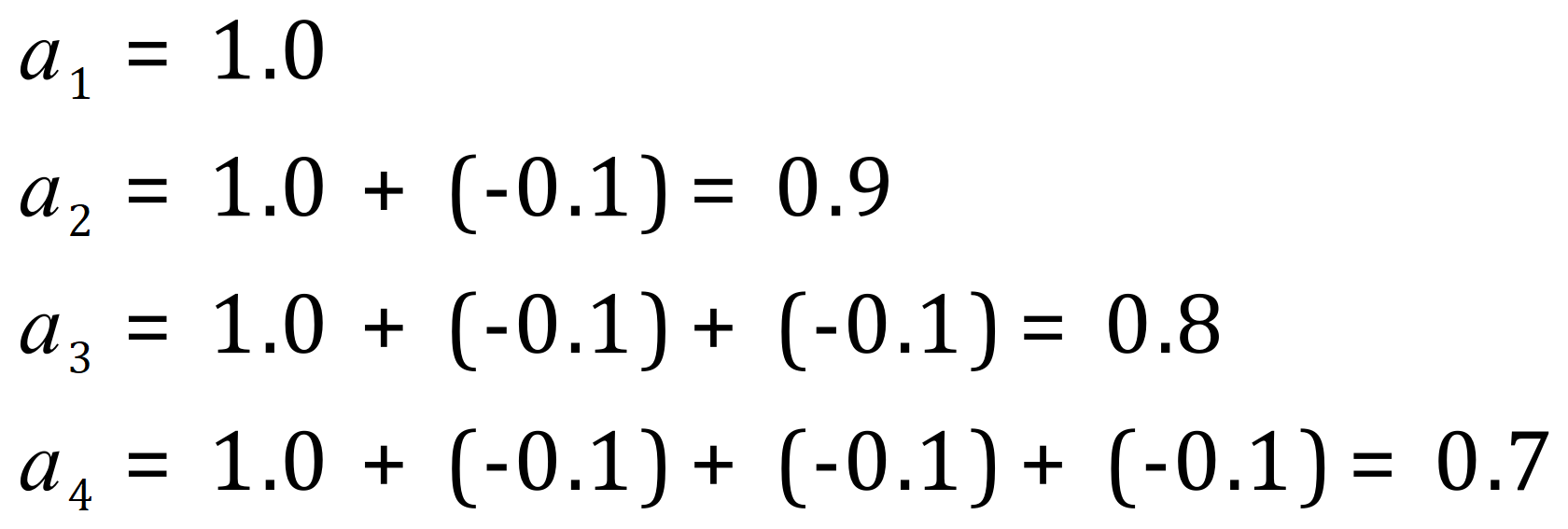
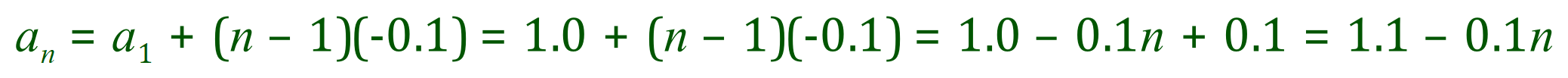
Therefore our closed form for this particular sequence is:
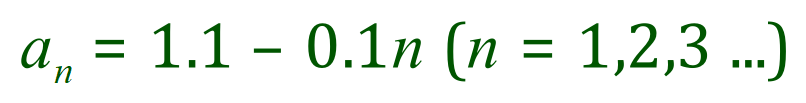
A general formula for an arithmetic progression is therefore:
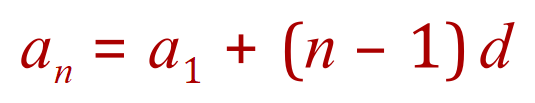
Note that when we talk about “arithmetic progression” we emphasise the ‘MET’ when pronouncing the word “arithmetic” ( arith-MET-ic).