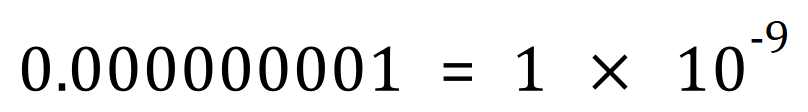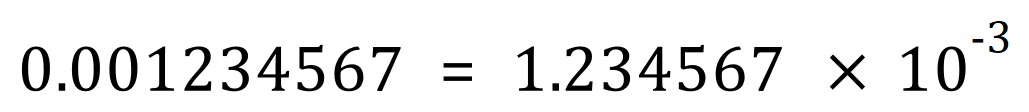Very Small Numbers in Standard Form
We have seen the use of Standard Form to represent very large numbers, where writing them out ‘long hand’ would lead to likely errors, e.g.: The Andromeda Galaxy is said to be two and a half million light years away (approximately):

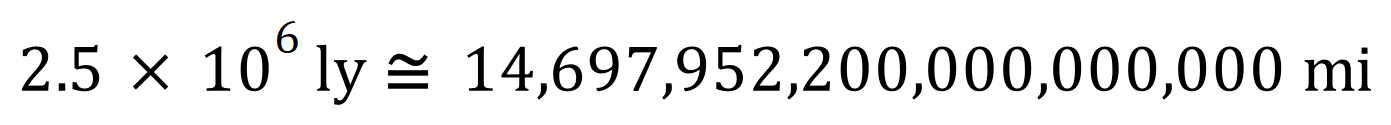
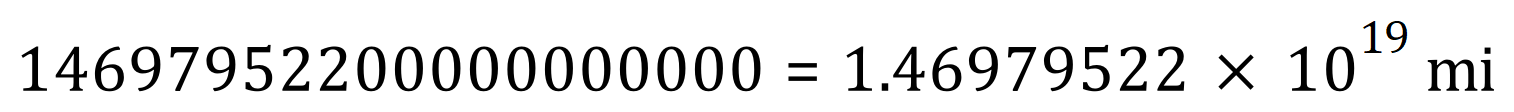
But what about sub atomic distances, or simply just very small numbers?

For example, the distance between the Sodium ions and Chlorine ions in the Sodium Chloride lattice is measured at approximately 0.28 nm (nanometres) which, in standard form, is:
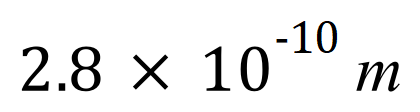
Although many scientific texts would write this as 0.28 x 10-9 metres, both of which would be correct, but the second seems to be favoured as it emphasises the ‘nanometre’ scale (10-10 relates to an older unit of measurement called the Angstrom).
So how do we work these out?
Well, let’s return to a slightly modified version of a previous diagram:
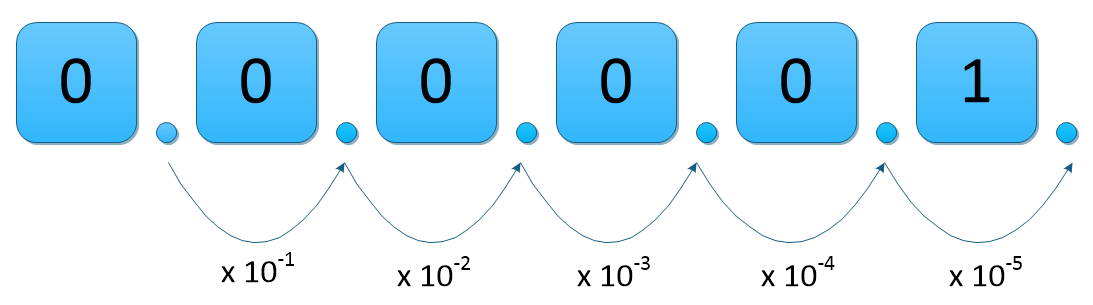
What this tells us is that the ‘ordinary number’ 0.00001 is in fact 0.00001 x 100 if you move again one point to the left (although this contravenes the rules of ‘standard form’) BUT as we move the decimal point to the right we pass through several more ‘misinterpretations ‘of standard form until we find the right one:
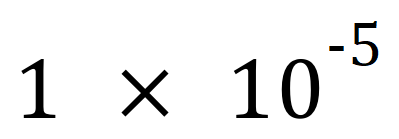
In essence, count the number of ‘zeroes’ / digits that appear to the left of the first non-zero number, insert the decimal point here then raise the ‘new’ number to a negative power of 10 which is one more than this: