Generally a large number is ‘broken down’ into two parts:

  • A decimal number  1<= and <10, 
  • Then multiplied by the number 10 raised to an appropriate power.



Let us look at an example…..

This number represents the speed of light in metres per second, and I have written it in the ‘usual way’ for numbers so that it can be read as “two hundred and ninety nine million, seven hundred and ninety two thousand, four hundred and fifty eight”, but for our trip down ‘standard form lane’ I need to rewrite it without the commas:

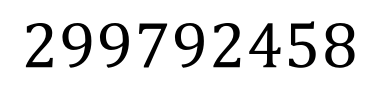
There is a decimal point to the right of the number 8, but it isn’t usually shown, to quote the speed of light to a decimal place would be meaningless because the precision of measurement would not justify it.

OK…..the rules say that the ‘decimal number part’ (or mantissa) should lie between 1 and 10, so we need to ‘shift the decimal point’ a certain number of places to the left so that we have a decimal number fitting the requirements of the rules.

The starting point for the decimal point is to the right of the number 8, but we have to move it a specific number of times to the left so that the resulting decimal is between 1 and 10. The diagram shows that we need to move the decimal point here EIGHT times to end up with:

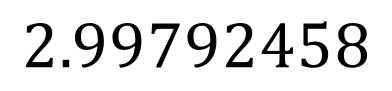
But this is a hundred million times smaller than what we started off with, so we multiply by 10 to the power of the number of ‘left shifts’ to get our standard form number:

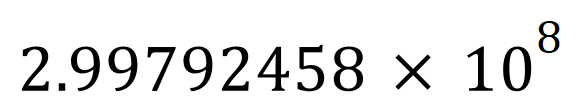
And this is how we represent standard form, on a calculator it is often the case that the 10x power notation will be shown as e+x (where ‘e’ means ‘exponent’ and the ‘x’ refers to the power of 10 being used).


Here are some more examples:


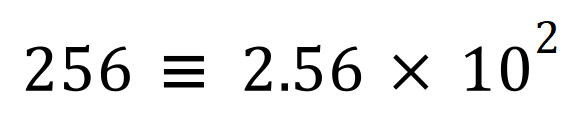
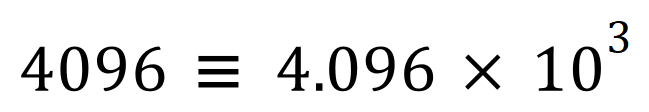
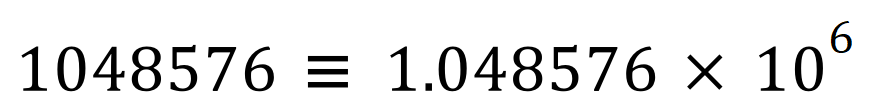
>> Questions <<