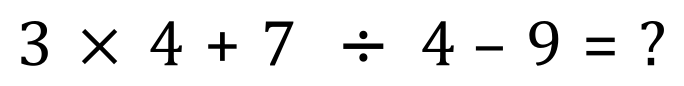BODMAS / BIDMAS / PEMDAS
There is a hierarchy, or an order in which the operations must be performed to arrive at the correct answer. This is known as "BODMAS" which you may see written as "BIDMAS" or even "PEMDAS" depending on the books you read. The latter one is American and stands for "parentheses, exponents, multiplication, division, addition, subtraction" and the second one stands for "brackets, indices, division, multiplication, addition, subtraction" but the version that seems to be favoured, at least here in England is the very first "BODMAS" which stands for "brackets, orders, division, multiplication, addition, subtraction".
This is the order in which the arithmetic operations are carried out to arrive at the correct answer, however life would be considerably less fun if there weren't complications and so "BODMAS" throws in a little quirk where some of the operations are of equal importance (the way it is written suggests that brackets outrank orders, which outranks division, which outranks multiplication which then outranks addition and finally that outranks subtraction, but all is not as it seems!
|
|
looking at the diagram you can see that brackets outrank everything. Any expression contained in brackets must always be calculated before anything else, and then the result of that particular expression used in the remainder of the calculation. Let us dissect the 2nd expression:
1. First of all, do we have any bracketed expressions? We can see that we don't have anything in brackets, so we move onto the next part of the hierarchy which is "orders". 2. Orders are when we raise numbers to powers so for example 3 raised to the power of 2 (3 squared) would be 9. In our particular example here we have no orders either, so we move onto the next step. 3. Looking at the diagram, division and multiplication appear to equal each other in hierarchy or importance, when we have a division on its own, we work it out next. When we have a multiplication its own, we work that out next. when we have examples of both present we work from left to right. In this case 3×4 = 12 and 7÷4 = 1 .75. 4. Look at the diagram again, apply the same rules to addition and subtraction as we did for multiplication and division, that is if they appear singularly, they are executed after any divisions or multiplications, if they appear together they are executed left to right. In the case above we have 12+1.75-9= 4.75 This is a simple example of the BODMAS rule, and it can become very complicated indeed. |
Let's take a look at quite a tricky example, one that you might even have to study for a while before you even start on it:
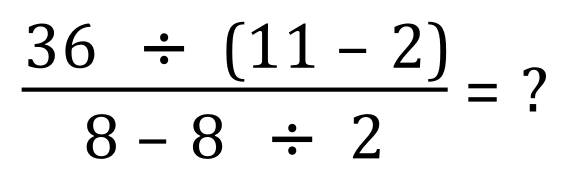
Don't be put off by this, follow the rules according to the diagram above and you will not go wrong.
Step 1 - brackets? Do we have any brackets? Yes we do, so we evaluate them first. If it helps rewrite the expression at each stage showing the "stage or step evaluations" at each point, so for example because we have executed the brackets the expression would now look like this:

Step 2 - orders? Do we have any orders/powers?, Well no we don't so we move on to step 3
Step 3 - divisions? Do we have any divisions? Yes we do, we have 36÷9 and we have 8 divided by 2. this makes our expression look like:
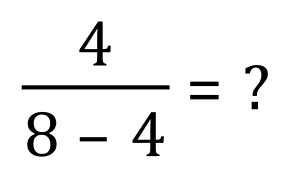
Step 4 - multiplications? Do we have any multiplications? No we don't.
Step 5 - additions? Do we have any additions? No we don't so we move on to step 6
Step 6 - we have one subtraction, 8-4 which is of course 4.
The final step (which I don't think I need to write down) shows 4÷4 which equals 1. So the answer to our problem is this:
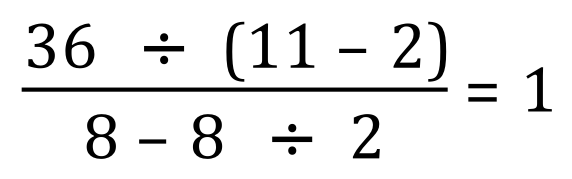
With BODMAS then, the order of precedence is this:
1. Brackets/parentheses are always executed first.
2. Orders/powers will be executed next.
3. Division and multiplication carry equal weight and will be executed from left to right if more than one of each example exists in the problem.
4. Addition and subtraction carry equal weight and will be executed again from left to right if more than one of each example exists in the problem.
>> Questions <<