Calculations and Hierarchy
Starting off this section quite simply, we will look at calculations. Many people make simple mistakes with regard to calculations and I believe that this has led to a dependence on calculators which could be avoided if some simple rules were applied. If you have an expression such as 3 x 4 you will almost certainly come to the conclusion that the answer is 12 and that would be correct, but what if we complicated matters slightly by adding in another operator such as "plus" and made our expression 3 x 4 + 7.
What would be the answer to this question?
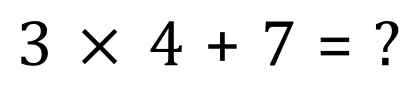
The correct answer is of course 19, but someone could just as easily work it out as 33 depending on the order that the multiplication and addition were carried out. If we do the multiplication first we end up with 12+7 which is of course 19, but if we do the addition first we end up with 3×11 which is 33, which one is correct? Put this calculation as you see it into your calculator and see which answer you arrive at. You should find that the calculator returns 19 which is correct, you should be able to see that the reason it returns 19 is that it performs the multiplication before the addition.
What would be the answer to this question?
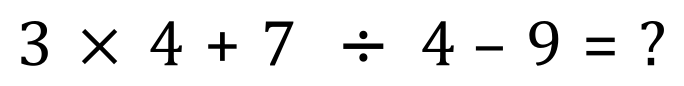
Put this into a calculator, see what you come up with.
You should return with an answer of 4.75 but again this depends on the order in which you perform the operations. If you perform the operations from left to right you might end up with -4.25, if you do the addition and subtraction before the multiplication and division you would end up with 3×11 divided by -5 which is -6.6.
As you can see this can get quite confusing, but the good old calculator will always return 4.75, why is this?, How does the calculator know what to do?