Compound Interest and Decay
We will remain with "The Multiplier" when we enter another useful feature of percentage calculations....interest and decay.
When we save money, or when we borrow money, there is usually "interest" to be taken into account. On savings this interest is what makes it worthwhile to save, your money grows and you see the benefit of the return. When we borrow money, for example a bank loan or a mortgage it is usually done on the understanding that the lender will charge "interest", in other words a fee for the privilege of borrowing from them. Interest rates are percentage values (which we can use as multipliers) and these determine the amount of extra money we pay back over and above the amount borrowed.
Example:
If I deposit £100 into a savings account which has an interest rate of 5% (usually quoted as per annum, which means each year) I would expect, after a year my money to have increased by 5%:

Don't worry at this stage about the £'s, I've left them out simply as a convenience.
The blue 100 is the initial amount that I deposited, the red 100×0.05 is the multiplier which determines the amount of interest, with 0.05 being 5% represented as a decimal number. The green 105 is the final amount that I'll have in my account after the first year.
Now, if I choose to leave my money in the bank for a second year, at the same interest rate I will receive more interest than I did the first time round. The reason for this is that I will now receive 5% of 105 in the second year, whereas in the first year I received 5% of 100. This means that my interest has "compounded":

In the first year I received £5 interest, in the second year I effectively received £5.25, this would increase even more in year three:
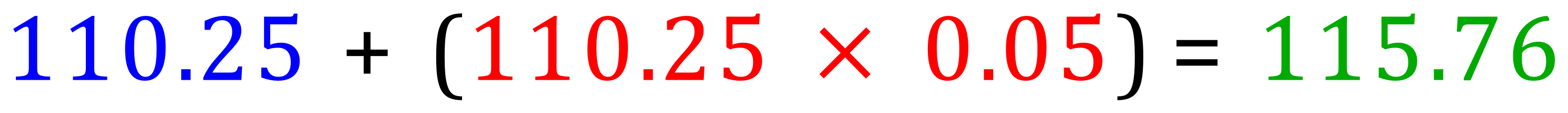
In year three my money increased by £5.51, in year two £5.25 year one £5 only. So, you can see that compound interest increases slightly every year over and above what it was the previous year. The arithmetic behind this is quite straightforward but it will become tedious if you wanted to know for example how much money you would have in the bank after 25 years. You would not want to multiply out from year 4 to year 25 inclusive, although you would probably come up with the right answer it would take you a very long time and is prone to computational errors.
Mathematicians try to get around these problems by producing "rules" or "formulae", and there is one for "compound interest" and of course "compound decay"which we will come to later.
The formula for compound interest is:
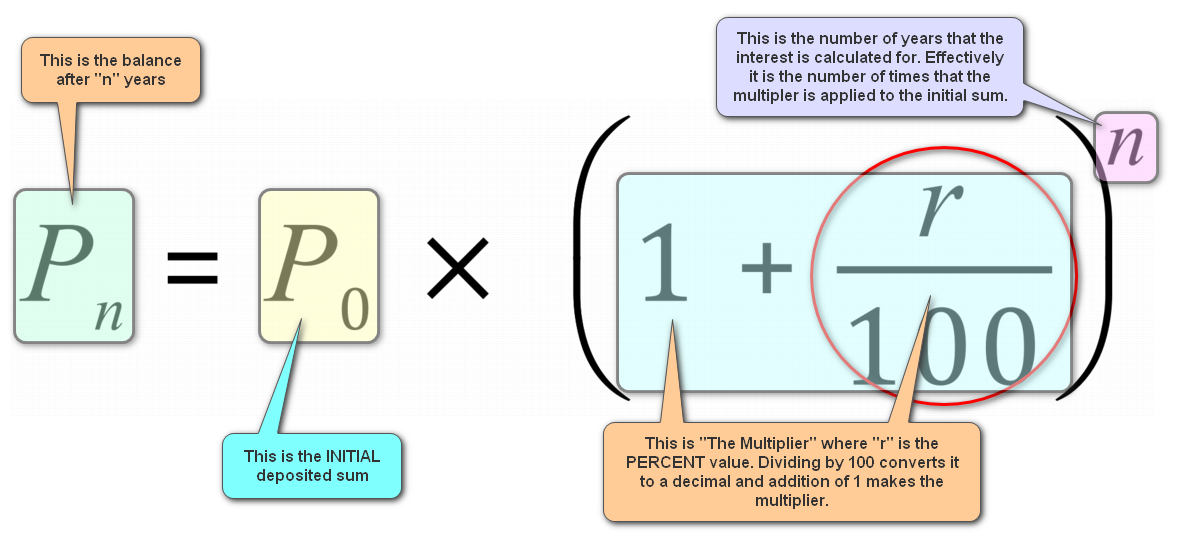
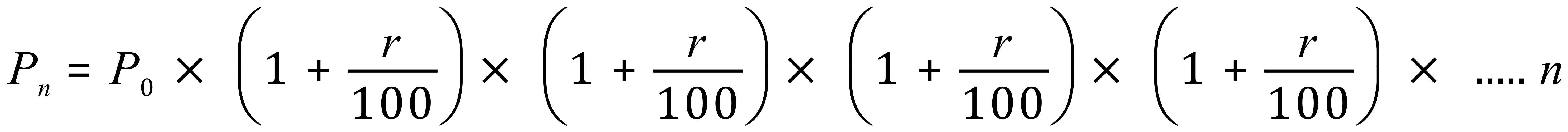
Exercise:
Q1. A bank pays 3% per annum compound interest, calculate how much interest will be earned in the following accounts:
- £250 deposited for one year
- £45 deposited for three years
- £100 deposited for two years
- £1500 deposited for four years
A1a.
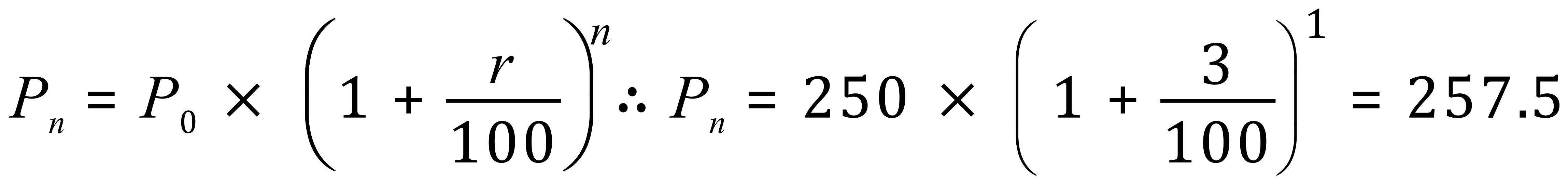
Therefore the interest would be £7.50 over 1 year.
A1b.

Therefore the interest would be £4.17 over 3 years
A1c.

Therefore the interest would be £6.09 over 2 years.
A1d.

Therefore the interest would be £188.26 over 4 years.
There are two important things to remember here:
- State the answer, appropriately rounded after all of the calculations have been done.
- State the answer you have been asked for, in these cases although we have calculated the final balance it is only the interest we have been asked for, therefore this is all you would quote in your answer.
>> Questions <<