Bases Other Than 10
When we talk about bases, we are talking about that numerical value upon which a “counting system” is built on.
For example for many years we have used base 10 as the essence of our counting system, we count from 1, 2, 3… and up to 9 and we reach 9 we call what we have already “10” and we move on to another “10”.

If you take a look at the picture above and imagine it as, say for example, an egg box you would be able to fit 10 eggs into it in the holes marked 1 to 10 inclusive, after which you would need to start on another egg box and when you’d filled that (having 20 eggs now) it start on the third box and so on.
Because we choose to use boxes that respectively hold 10 eggs we can say that 10 is the base of this particular numbering system.
When we fill our tenth box, we have 10 boxes of 10 eggs and we call this 100, when we have ten 100s we call this 1000, then 10,000, then 100,000 and so on.
You should be able to see that to move from 10 to 100 we multiply by 10, and to move from 100 to 1000 we again multiply by 10, in fact to move “up the base” we multiply by the base value, in this case, 10.

The diagram above shows the “movements up the base” or to put it more correctly the “orders of magnitude” of the base, we start off with units 0 to 9 and then when we reach 10 we move into the next column of tens, then hundreds, then thousands and so on. Although it isn’t particularly well drawn in the diagram the expression N^0 actually means the base raised to the appropriate power, so 10 raised to the power of 0 is of course one which is the column heading for “units”. 10 raised to the power of 1 is in fact 10 which becomes the column header for the tens column likewise 10 raised to the power of 2 is 100 which becomes the column header for the hundreds column and so on.
Simply put, to move up and down the “orders of magnitude” of the base, multiply or divide by the value of the base.
What I suggest you do now is to study the last page very carefully before you move on, just to make sure that you’ve really got the grasp of it because now we are going to take a look at a base that is used widely in mathematics and computing, that is the base called “binary” or base 2 and this is a little bit more complicated:

Just like in the previous picture the heading says HTU, but strictly speaking in any base other than 10 it’s not accurate so please just ignore that.
What should be significant is the expressions “N raised to the power of…” Because this is how we move, once again “up the base” in binary. Consider the values on the next line:
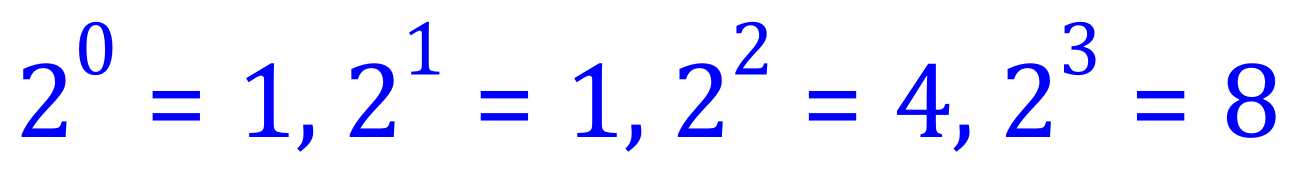
2 to the power of 0 is in fact one, 2 to the power of 1 is 2, 2 to the power of 2 is 4 and so on. You can see, just like in the case of the decimal system to move up the orders of magnitude we multiply by the base and conversely to move down the orders we divide by the base. Look at the numbers in the second row and you should be able to see that moving from right to left they double and moving back from left to right they halve.
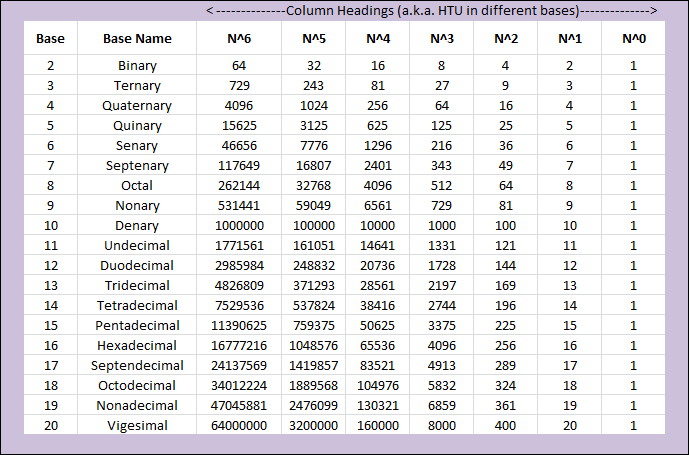
The diagram below is a complete table of all bases up to “base 20”, there are many more but I don’t intend to discuss them here.
Okay, so how do we move from one base to another? Well before we go into that let’s take a look at the way that we signify what base a particular number represents.

Consider the number I have typed above, what would you say it was?
Of course, I do hear you say “well it’s 25!” And in at least one case you would be correct. The number is indeed 25 if you considered it to be a base 10 number. For reasons that I will explain shortly it cannot belong to any base lower than 6, so in fact our number which correctly ought to be pronounced “two five” could be a base 10 number, a base 9 number, a base 8 number or a base 7 or 6 number. Not only that it could be any base higher than 10 and the way that we differentiate between bases is that we apply the base as a suffix/subscript like this:
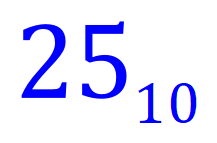
When you see a number written like this you know that it is in fact 25 represented in base 10 or denary. (The subscript won’t necessarily be quite so big, but to avoid confusion it should be there in some shape or other). Now that I’ve shown you what a number would look like in its respective base, have a look at this number and see if you can work out what it is:
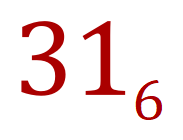
Yes, you’re right it’s the number “31” (three one) represented as a base 6 number, the temptation now is for you to say to yourself “okay, what is it in base 10?”, well it is in fact 19 as a decimal number:

In the next few pages I am going to go through how we convert base X to base 10 and vice versa.