We will leave this particular section with a brief discussion of powers.

If we return briefly to our expression:

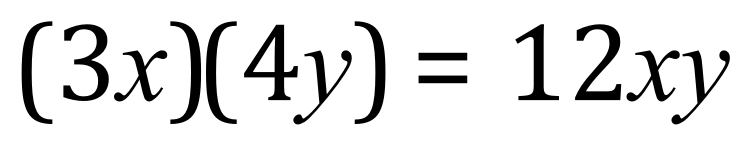
But this time we have only X values:

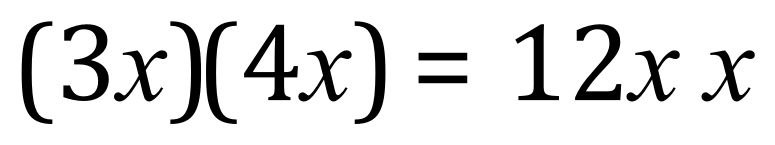
This is correct but wouldn’t be left that way, instead when we multiply a variable by itself we denote this as a representation of a ‘power of that variable’

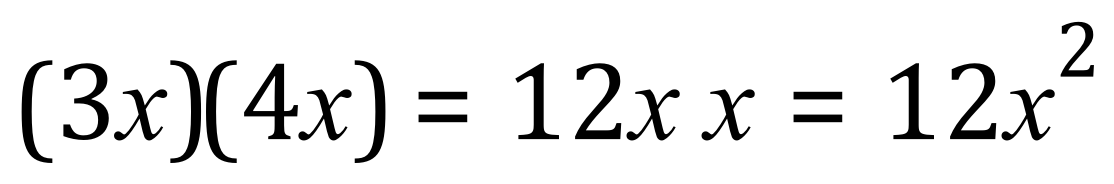
Where the ‘superscript two’ denotes “squared”, we have been able to tidy up a little bit by showing the resultant value of X in its “power” format. Phonetically the above equation would be read out like this:

“Three ecks times four ecks equals twelve ecks squared”

Let us move on:

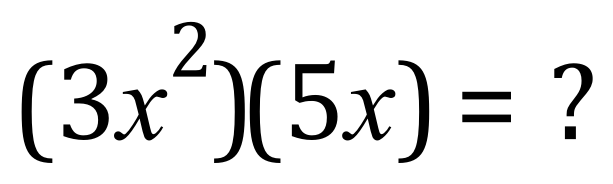
Okay, this one is a little bit more complicated because it involves a squared power before we have even worked everything out. 3×5 as you have probably gathered is quite easy to work out as 15:

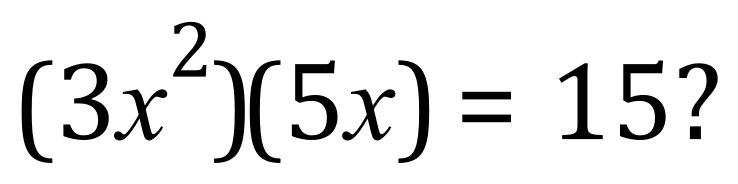
But what do we do with the X values? Well, one way to look at it is if we expand the left-hand side of the equation:

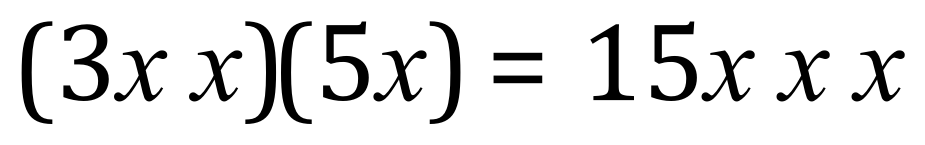
By counting the number of X’s that we end up with we do in fact come to the right answer, but of course we would not write it this way, instead we would choose another power of X known as “cubed”:


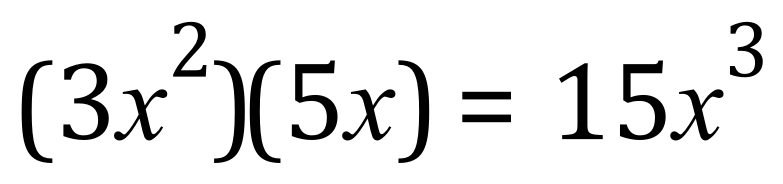
“Three ecks squared times five ecks equals fifteen ecks cubed”

Before I let you into a little secret, let us just take a look at one more example:

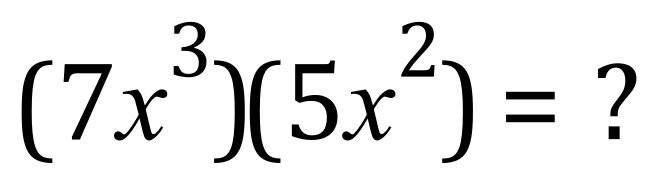
Just as we did previously, we can work this out by expansion:

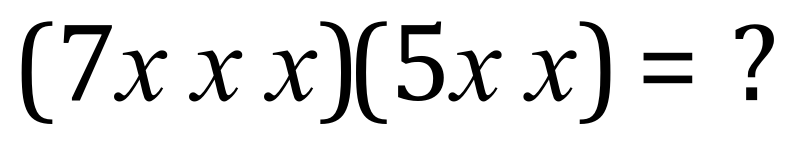
Again the constant ‘coefficients’ come to 35 but what about the X values? Well add them up:

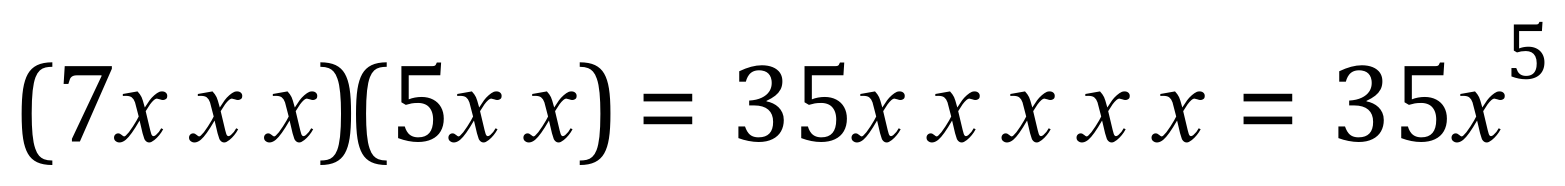
“Seven ecks cubed times five ecks squared equals thirty five ecks to the fifth”

The secret? - What we are doing is adding up the powers or the index of each value of X, in multiplication of variables raised to powers we add the powers, so the equation above could just as easily have been written like this:

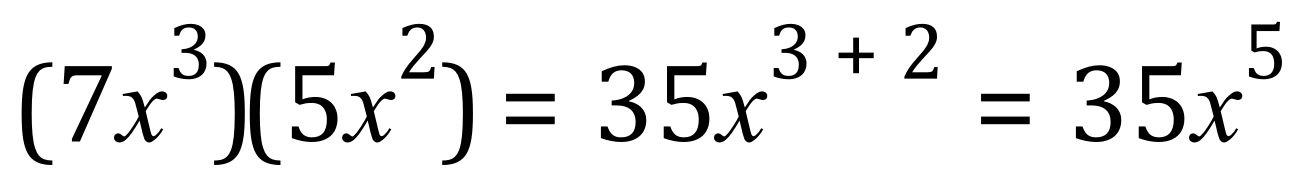
You can see, I’m sure, the advantage of being able to simply add up the powers rather than having to keep expanding each indexed power of X, for example imagine having to work this expression out by expansion:

Division

The rules for division are quite similar to those for multiplication, but in this case we do not add the index powers, we take one away from the other, that is, we subtract.

We will stick with our first equation but this time instead of a multiplier it will become a divisor:

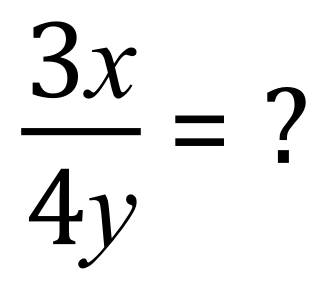
Well, in this case because we are dealing with dissimilar variables we cannot go any further, but take a look at this example:

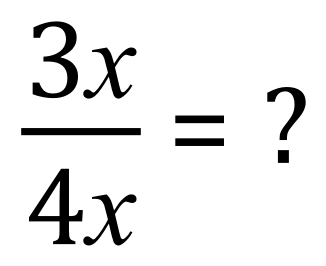
Remembering from our discussion on index / powers or indices these expressions are the same although the index of one is not normally shown:


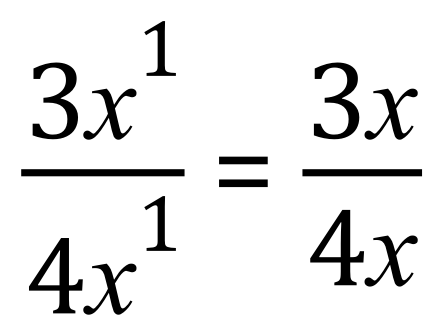
So, in this case if we take the lower index power (that is the one on the denominator) away from the index power of the numerator we end up with zero, in other words X vanishes:

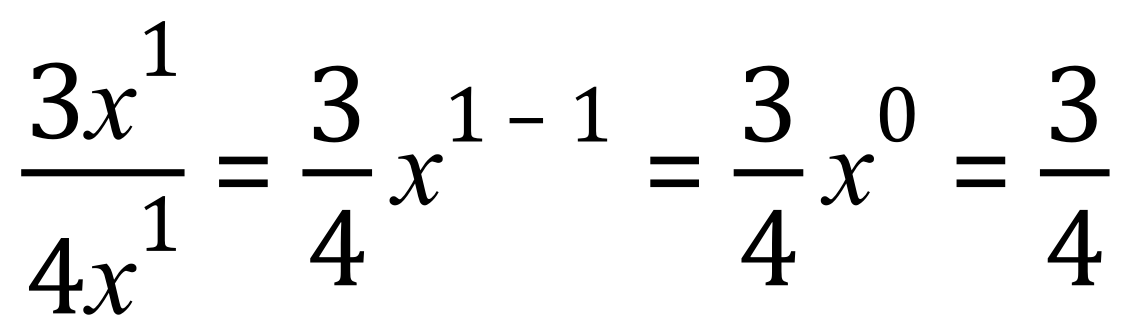
Once again, we could expand our powers of X and simply ‘cancel down’ to see what we have left at the end of that procedure, for example have a look at this one:

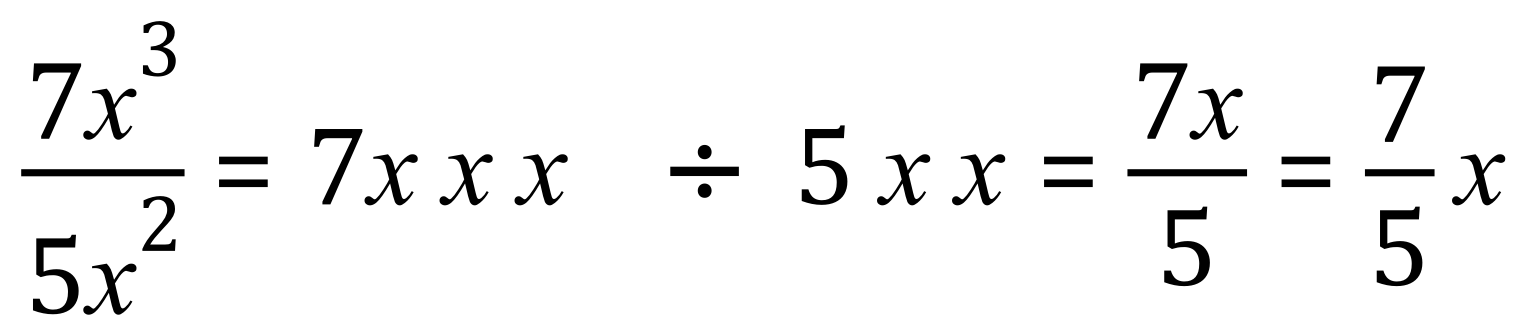
Note that it is also OK to call this but generally with fractions it is accepted to leave them as they are, even if they are ‘top heavy’ or ‘improper’.

Note: The subtraction MUST always be from the ‘top to bottom’, i.e.: the power of X on the denominator is taken from the power of X on the numerator, or ‘top power minus bottom power’:

With multiplication of index powers, involving addition it doesn’t matter:

But division of powers, involving subtraction, does matter:

In mathematics, multiplication and addition are "commutative" which means that they can be performed in any order, for example 3x4 will give you the same result as 4×3 and 3+4 will give you the same result as 4+3.


Subtraction and division are not commutative as 3-4 is not the same as 4-3, and 3÷4 is not the same as 4÷3.