Algebraic Division
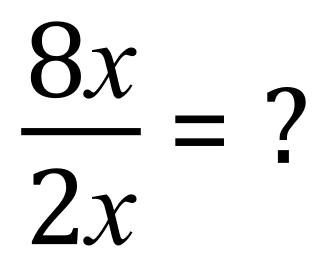
In this simple fraction, 8X is referred to as the numerator and 2X is the denominator. If you recall above 8X means “eight times X” and of course 2X means “two times X”. Because we have X above and below the ‘fraction line’ or ‘Vinculum’ they cancel each other out, leaving just the numerical values, the result of the expression then becomes four:
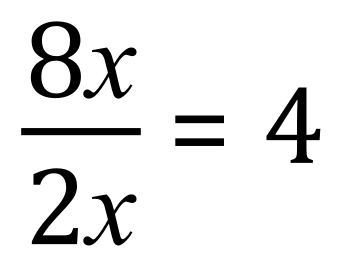
Of course the situation is not the same here:

We can’t have a ‘hard and fast’ answer such as 4, because we still have a variable amount ‘X’ that has not been ‘cancelled out’ this time. Now then, on the subject of 'cancelling out' it is good practice to try to simplify the expression as much as possible.
Consider this example:
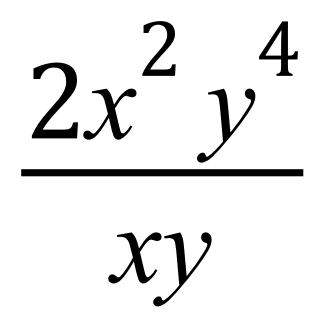
How can we simplify this? Take a look at the 2x^2 and consider the fact that there is an 'x' in the denominator. If you multiply something by a number, then divide the answer by that same number, you will return to where you started:
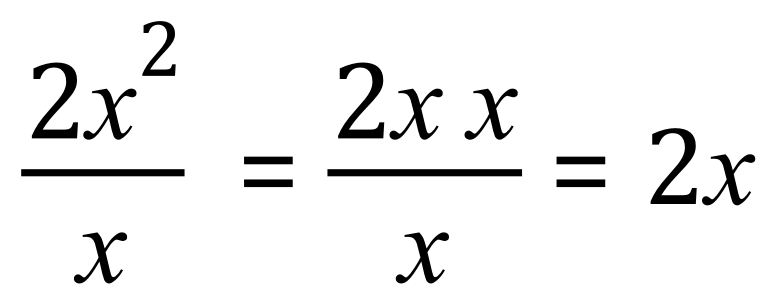
Note that one of the 'x' at the top will 'cancel out' the one on the bottom, to leave a simple answer of 2x. Use numbers to prove this to yourself, let x = 3 for example and you would have this:

Study this example and see if you can follow it.
Now...back to the original question:
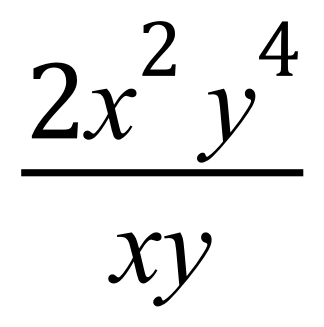
Although it would be unweildly to do so in most cases, expand the terms and see if there are any that can be cancelled out:
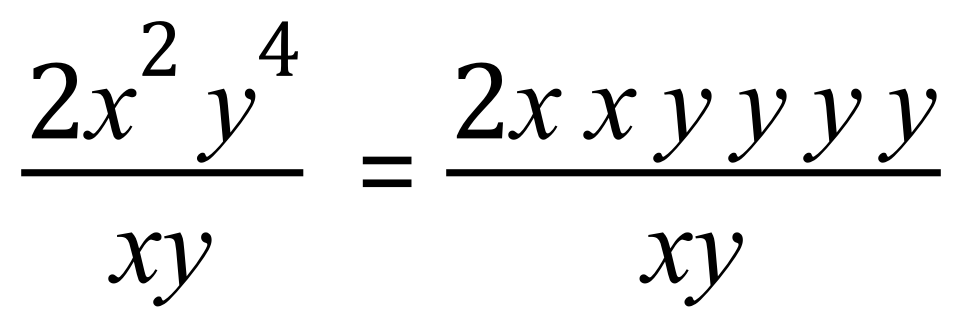
We can cancel out at least one of the 'x' and one of the 'y' to leave an expression which is no longer a fraction, this is always a nice place to be:
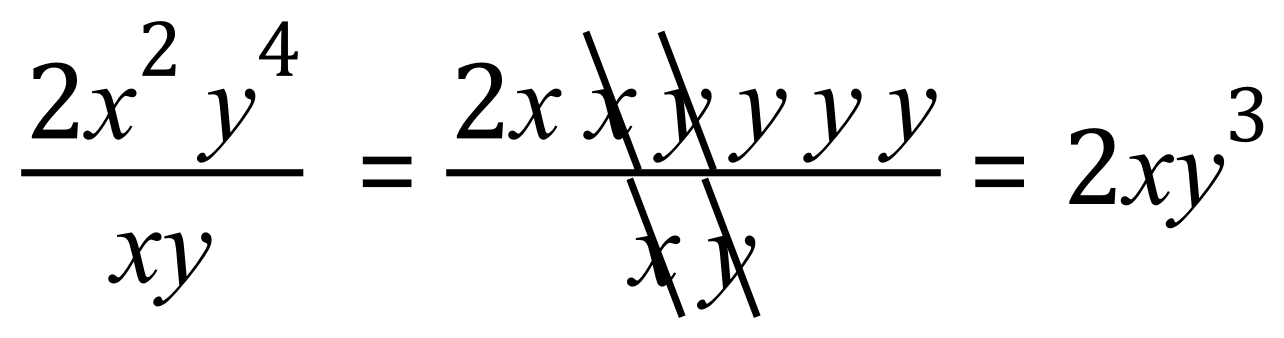
Algebraic division can be complicated, especially when quadratic expressions are involved. In these cases, we have to check to see if any factorisation can be done. If it can, perform the factorisation and then look for common factors on the numerator and the denominator which can be cancelled out then further simplify the expression if possible to arrive at the simplest possible result.
Let's take a look at an example:
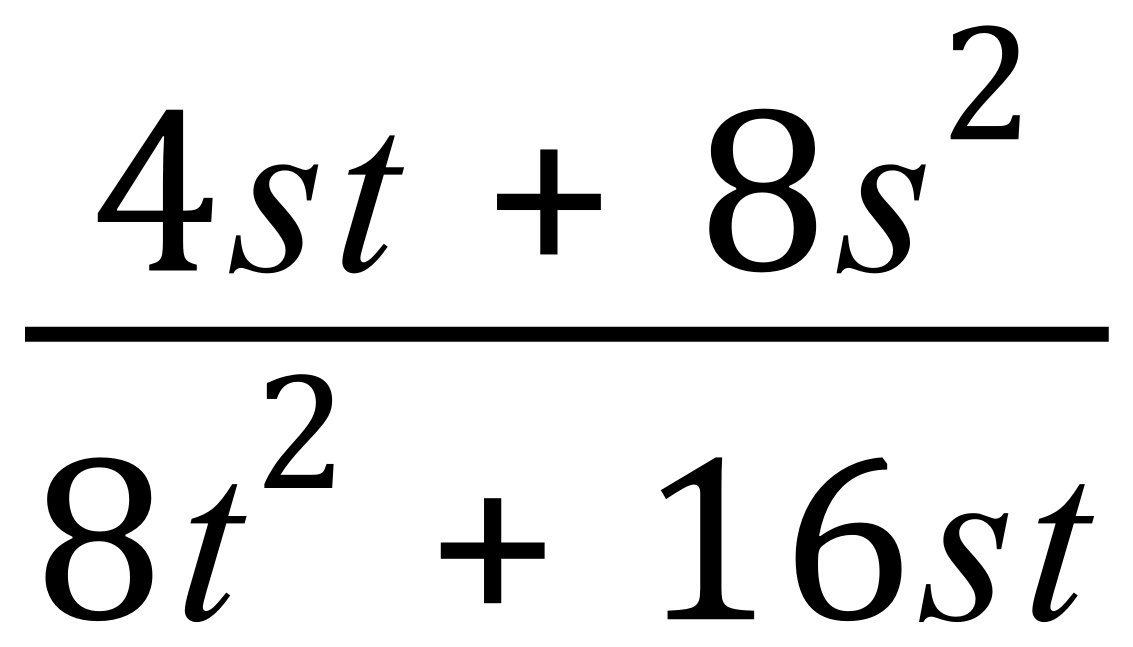
This looks like a fairly beastly example, but if you're already pretty switched on with algebra, you will be able to see that factorisation can take place in the numerator and the denominator, let's see how this will be done:
There is a common factor in the numerator of 4s, and in the denominator we can see that there is a common factor of 8t:
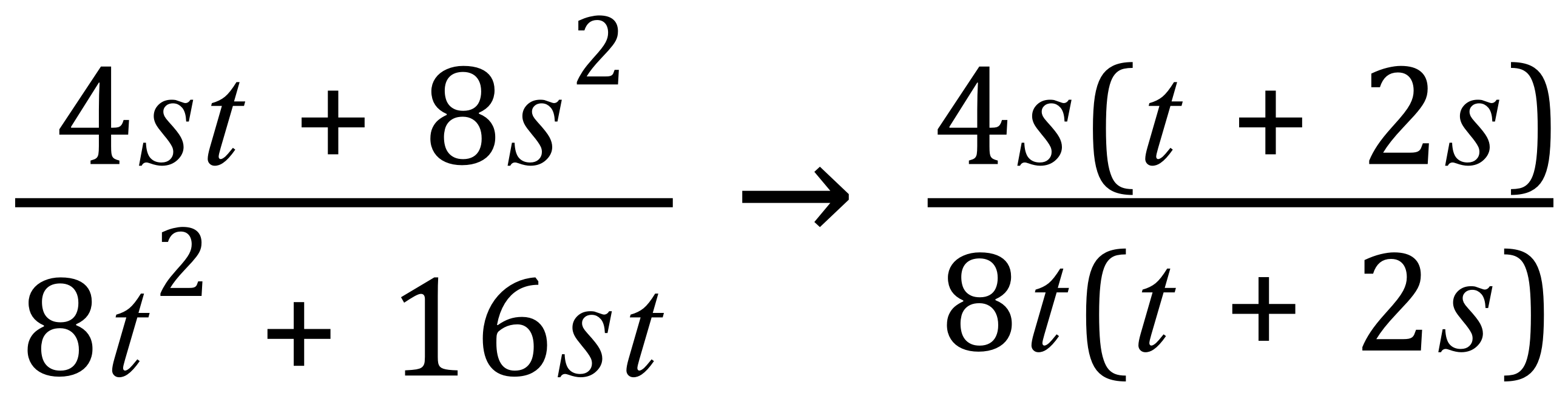
If we cancel out the common factor (t+ 2s) we can then simplify what is left, we will end up with this expression which is as far as we can go:
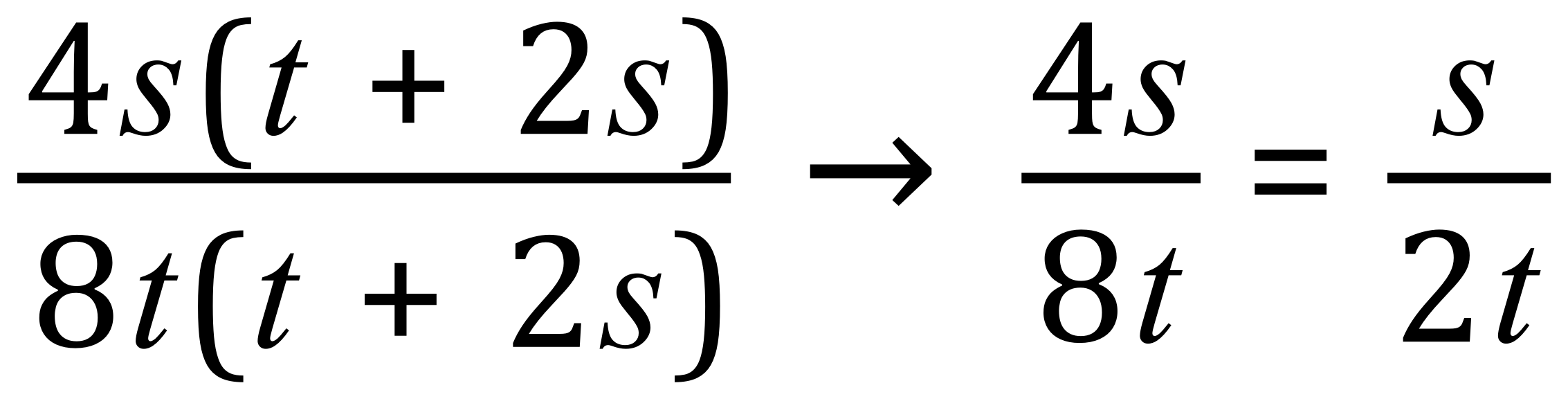
>> Questions <<