Binary Fission
The process of binary fission is used by prokaryotic cells such as bacteria to replicate, a simple type of cell division which results in the cell making copies of its genetic material before it splits into two daughter cells. The steps of binary fission, you should be familiar with but will be repeated here for ease of reference:
1. The circular DNA and plasmids replicate, remembering that these type of cells do not have a true nucleus, but a single circular strand of DNA floating around in the cytoplasm.
2. After the replication above, the cell gets bigger and bigger and the circular DNA strands move to opposite ends of the cell.
3. The cytoplasm begins to divide and a new cell wall begins to form.
4. The cytoplasm completely divides and two daughter cells are produced, each daughter cell has one copy of the circular DNA but may have a variable number of copies of the plasmids.
Bacteria can divide very quickly if the conditions are right, for example given the right conditions the bacteria E.Coli can replicate itself in as little as 20 minutes.However if the condition start to become unfavourable the cells will stop dividing and start to die off. The bacteria replicates at a rate depending on the environment and the type of bacteria, a measurement known as the "mean division time" is used to estimate the number of bacteria in a population after a given time. For this to be calculated we need to know the average time it takes for a bacterial cell to divide, in other words its "mean division time".
Exactly how the mean division time is calculated in the first place is beyond the intentions of this particular chapter, the idea of the questions in this chapter is to enable you to become familiar with the mathematics involved in calculating the size of bacterial populations after a given time. The calculations essentially involve binary arithmetic as the expression binary fission would hopefully have suggested to you.
Let's take a look at the calculation involving these new concepts:
Q. A certain observed bacteria was found to have a mean division time of 40 minutes. How many cells would the bacteria produce after a period of 12 hours?
A. The first thing we should do is make sure that we have our times in the same units either hours or minutes, because the given mean division time is less than one hour it is probably better that we work entirely in minutes for this calculation. So in this case we have a mean division time of 40 minutes in the period of 720 minutes.
If we divide our total time of 720 minutes by a mean division time of 40 we find that in the time given we would have 18 replications. After the first replication we would have 2 bacterial cells, then after the next replication we would have 4 then 8 then 16 and so on. Using Powers notation which you will have learnt about in a different part of this book, we calculate the final number of bacteria produced by raising 2 to the power of the number of divisions, in other words in this particular case 2^18 = 262,144. We can see then that in even such a short period of 12 hours we have amassed over a quarter of a million bacteria!
Q. After experimentation, a scientist has calculated that a particular bacteria has a mean division time of 30 minutes.
(a) how long will it take for one of these bacteria to produce a population of 128, State you answer in hours or minutes.
A.
(a ) We know that binary fission means that the cell halves / that is it splits in two / that means it doubles and we are given an expected end population of 128 cells. We are told that the mean division time is 30 minutes and so what we are looking for is the number of divisions, each of 30 minutes, that will result in the end with the required number of cells.
Starting with 1 cell, after 30 minutes we have 2 cells, after 60 minutes we have 4 cells, after 90 minutes we have 8 cells, after 120 minutes we have 16 cells, after 150 minutes we have 32 cells, after 180 minutes we have 64 cells and finally after 210 minutes we have our required 128 cells. 210 minutes is 3 1/2 hours. It was fairly straightforward to step through this one, but it can become quite laborious if you're talking about short division times and very large populations. In this case we should consider perhaps deferring to a more mathematical approach using the binary system and logarithms. Let's take a look at another question where our main division time is a lot shorter and we're looking at a much greater population.
Q. Our somewhat keen and eager scientist has also calculated that a separate bacteria, somewhat more virulent has a mean division time of only 10 minutes. The scientist is eager to calculate how long it would take for this bacteria to multiply into its trillions, in particular 140 737 488 355 328 as a population size which would clearly be problematic.
A. We need to establish how many divisions and then multiply this by 10 to give us the time factor. If we call our division 'n' we can see that after one division (n = 1) we have two cells, and in our particular example here that would have taken 10 minutes. At the second division (n = 2) we would have 4 cells in the total time of only 20 minutes and at a third division (n = 3) we would have 8 eight cells, having taken only 30 minutes to get here. Can you see a pattern forming in these numbers?
Let's just step back one-minute. We start with 1 cell, and after the first division we have 2 cells, and we know from our mathematics that 2 raised the power of 1 is 2:
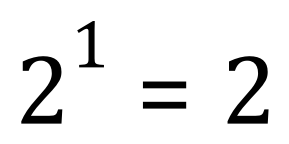
What happens with our next division, when the second division takes place? Well we end up with 4 cells which we can represent in a similar sort of way as above:
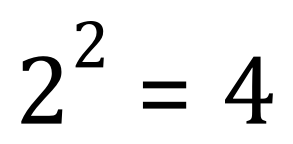
At the end of our third binary fission/division we end up with 8 cells, can you now see the pattern forming? Take a few minutes and look at it.
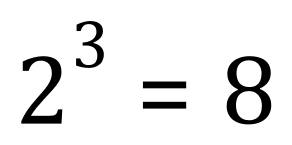
The correlation between the three equations that you can see is that if you raise the number 2 to a power equal to the number of the division, for example in the last case 3 you end up with a result which is the number of cells which exist after that division, in this case 8.
Let the number of the division equal 'n', and the number of cells after that particular division equal 'N', you should be able to see where the following expression comes from:
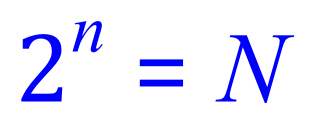
According to this equation, if we are given the number of divisions we should be able to calculate the number of cells that will be produced at the end of the last division, similarly if we are given the number of cells that are produced we should be able to calculate how many divisions and therefore the time if we are given a mean division time as well. The first part of the problem is quite straightforward for example if we are given n = 6 we can quickly establish that the number of cells after the 6th division would be 64.
Let's go back to the question above which at this point remains unanswered, our somewhat eager and keen scientist is looking at a population of almost 141,000,000,000,000 cells (the exact number is of course stated in the question) and we need to calculate how long it would take for this population to arrive given our mean division time of ten minutes in the case of this particularly nasty bacteria. Well, what we are given is the mean division time, what we are not given is the number of divisions required because to establish the answer to the question, how long it would take for this population to be produced we need to know how many divisions we have multiplied by the mean division time (10 minutes).
Establishing this mathematically we would arrive at an expression like this:

To establish the value for n we will use a feature on your calculator which you may or may not be familiar with, "ln" which is logarithm to the base to, or naperian logarithms. In logarithmic form the above equation becomes:
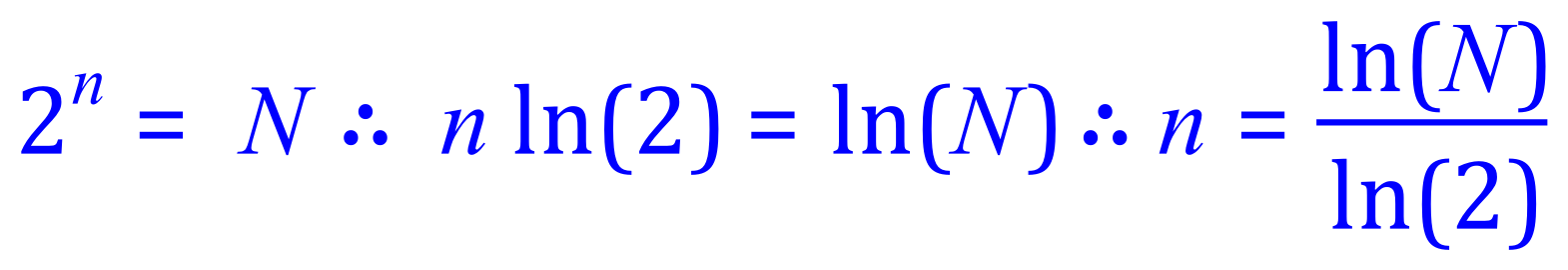
This somewhat confusing looking equation is really quite simple, what it is saying is that if we take the logarithm of the number of cells and divide it by the logarithm of two we will end up with a number which represents the number of divisions that took place to get there. Let's use one of our simpler equations first of all where we know the answer for example after 3 divisions we would have 8 cells. As is the case in many questions, let's just "plug and go":
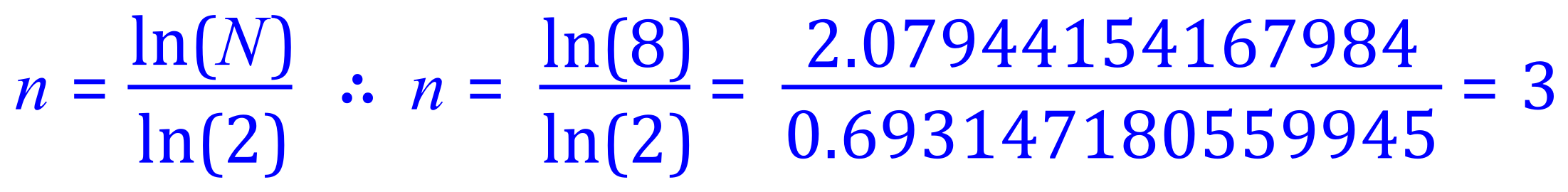
And we know that this is the case because for the cell to produce a population of 8 it must divide 3 times!
Now will finally return to our question where the number of cells is in the trillions, but we act no differently and simply substitute the numbers we are given into the equation. If you are familiar with the workings of your calculator there is no reason why this type of question should ever be of concern to you.

From this calculation we can see that to reach population of 140+ trillion as the question states, we would require 47 binary divisions. We are told that the mean division time is 10 minutes in the question and so it's a straightforward calculation of 47×10 = 470 minutes (or approximately 7.83 hours).