Inhibition Zones
When we are investigating the effect of antibiotics on the growth of bacteria, a practical test would be to place paper discs soaked in different types of antibiotic, and of course at different strengths on a preprepared agar plate which is covered evenly with bacteria. If the antibiotic is working at all, you will start to notice a clear area around the paper where no bacteria can grow or have died as a result of the antibiotic present. These clear areas are known as "inhibition zones".
During these sorts of experiments it is usual to leave the antibiotic for up to 48 hours at a reasonable temperature (not too high, remember that high temperatures could possibly lead to the development of quite dangerous pathogens) and at the conclusion of the investigation, the size of the inhibition zones is measured in an attempt to gauge the effectiveness of the antibiotic. Often, large differences in the inhibition zones of different paper discs can easily be spotted, but the best method is by calculating the area of the inhibition zone. These are pretty basic calculations in geometry using familiar mathematical techniques so this section will not dwell on the point.
On the assumption that the inhibition zone is circular (and it probably will be), we use familiar formula for the area of a circle:
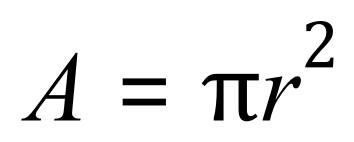
Where of course A is the area, the Greek letter 'pi' is the irrational number which represents the ratio of the circumference of a circle to its diameter, often quoted as 3.142 and 'r' is the radius of the circular inhibition zone.
Q. A student conducts an experiment and after 48 hours identifies two inhibition zones on his agar plate. The diameter of the first inhibition zone is 24 mm and that of the second inhibition zone is 32 mm. Calculate the areas of the respective inhibition zones.
A. Let us call the first inhibition zone (the 24 mm one) zone X and the second inhibition zone (the 32 mm one) zone Y. We must first take notice of the fact that we have been given diameters not radii so we need to halve each measurement to obtain the radius before we "plug in" the values into the equation above.

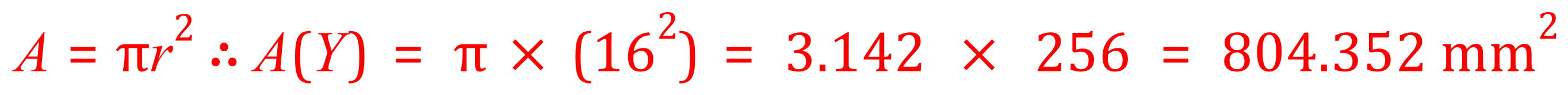
An interesting point to note is that although the inhibition zones aren't that different in diameter, there is a considerable difference in the area. Although we didn't do it in this particular case, always be wary of units requested and units given in the question which may or may not be the same thing and so may require some form of conversion!