Boyle's Law
As we know, the particles in a gas are constantly moving, in random directions and are constantly bouncing off each other and the walls of any container that they might be in. The energy of a gas particle, that is, the kinetic energy is given by the familiar formula for kinetic energy:
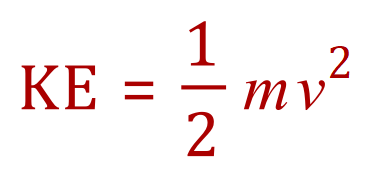
So we can tell from this equation that if the kinetic energy increases, then either the mass of the particle has increased or its velocity has increased. As the masses of gas particles don't seem to randomly increase or decrease we would attribute any increase in kinetic energy to an increase in velocity. So how can we increase the velocity of the particles?
If we increase the temperature of the gas, we transfer energy to the kinetic energy stores of the particles making up the gas, therefore by the argument previously as the mass of the particles remain unchanged, the velocity must increase as the energy does. You would be right in assuming that if we decrease the temperature the reverse applies.
We said that as the particles move around they collide and rebound off each other, and also collide with the walls of the container (cylinder, gas syringe or whatever you have the gas stored in) and these collisions apply a pressure to whatever they collide with (think about it, if you bump into a friend, the friend is likely to move in response to your accidental collision, if your friend doesn't move you are going to bounce off them).

The diagram above (which may, or may not be animated depending on which version of this book you are reading) shows gas particles moving freely in a fixed container, colliding with each other and the sides of the container, exerting pressure on the latter at each collision. This particular animation is also good at showing how diffusion works in gases (watch how the burgundy and grey particles get mixed together during collisions).
The relationship between volume and pressure in gases is quite straightforward, each is inversely proportional to the other, such that the product of the two remains constant:
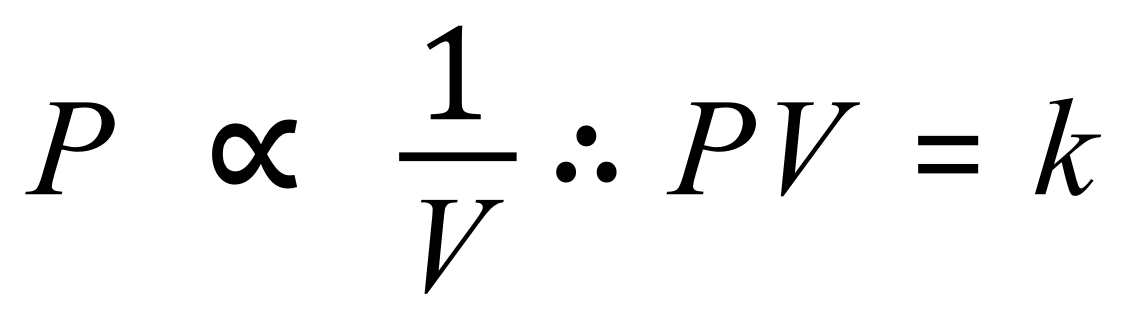
The above expression, which is the foundation of one of the gas laws "Boyle's Law" is valid for a fixed mass of gas at a fixed temperature, as a variance in temperature will also affect pressure.
Given the fact that the product of the pressure and the volume is constant, we can calculate the effect of varying one or the other parameter, let's take a look at an example to make this look a bit clearer:
Q. A fixed amount of gas is held in a sealed container which has a volume of 5 m³. The gas exerts pressure on the container of 200 Pa. Using some sort of compression system, the volume of gas is reduced to 2 m³, from this information calculate the new pressure of the gas on the walls of the container, in Pa.
A. First of all we need to make sure we keep our units consistent, the question gives us units which are already correct (cubic metres and Pascal) so we don't need to make any changes. From the equation pV = constant we can state that any increase or decrease in pressure or volume will make a commensurate increase or decrease in the other property such that the constant remains the same, or in other words:
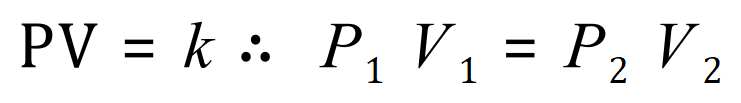
The question has asked us to find a value for the subsequent pressure (in this case P2) so we need to rearrange the expression in terms of P2:
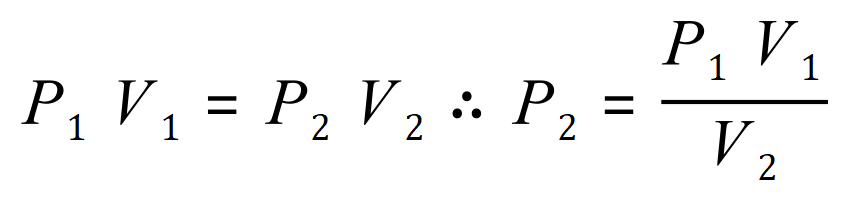
If we now substitute our unknown values for pressure and volume we can establish the new value for the pressure after the reduction in volume has been applied:
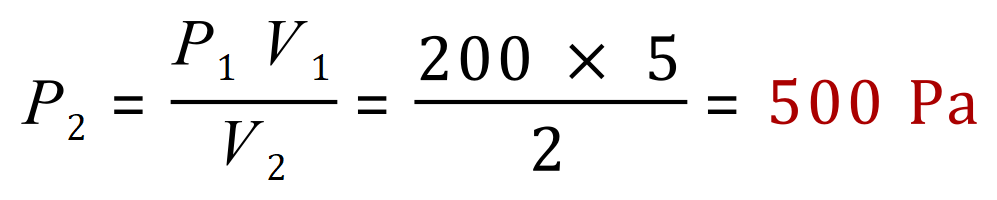
Boyle's law, also known as Marriotte's law, relates the pressure of a gas to its volume at a fixed temperature and mass. In a system with a fixed mass of gas at a constant temperature, Boyle's law states that the pressure of the gas is inversely proportional to its volume.
Keeping mass and temperature fixed, as the pressure of the gas is increased (say for example using a plunger) the volume will decrease and vice versa, in other words the product of pressure and the volume will remain constant.
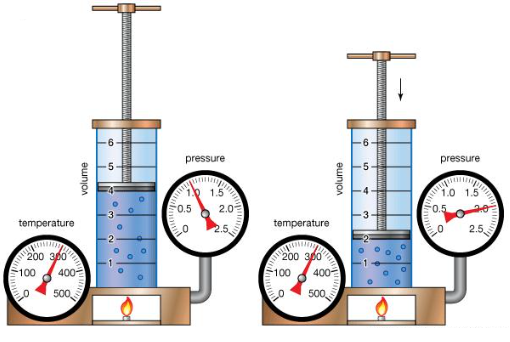
The diagram shows a fixed mass of gas (4 units) at a constant temperature of 300 units, the volume of the gas is reduced to 2 units with a commensurate increase in pressure from 1 unit to 2 unit with temperature remaining constant.
The equality here is obvious because 4×1 = 2×2, that is...pV = k