Chinese Stick Multiplication
Before we leave this section, we should perhaps give a little bit of thought to just how old some of these techniques really are. We learn addition, subtraction, multiplication and division from as early as the primary school years and we are just simply “handed down” these skills from our teachers almost exclusively without giving any thought to how we got there in the first place.
Just to finish of this section I’m going to go over an old method invented by the Chinese many many years ago which allows us to multiply numbers together using nothing more complicated than straight sticks, lines in the sand, scratches on the wall with a piece of chalk or anything when we can draw or otherwise create lines which cross over each other, that is lines which “intersect”.
Let’s take a very simple example to start with, say 2×5 which we know is 10 (if by this point in the book you don’t know that it’s 10 I think you might be in trouble :-)).
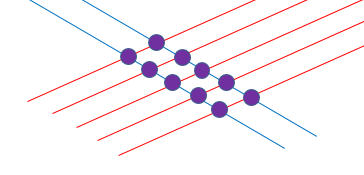
In the diagram above the 2 blue lines come down from top left to bottom right and the 5 red lines go from bottom left top right. The blue lines represent our 2 and the red lines represent our 5. The most important part is the intersections of these lines, each one being marked by a purple circle. If you count the purple circle you will see that there are 10 of them, from which we can conclude that 2×5 does indeed equal 10. The Chinese worked out very quickly this was an ideal method to perform multiplication and quickly expanded the method to include other larger numbers.
Let us take a look at another example, a little bit more complicated than the first one.
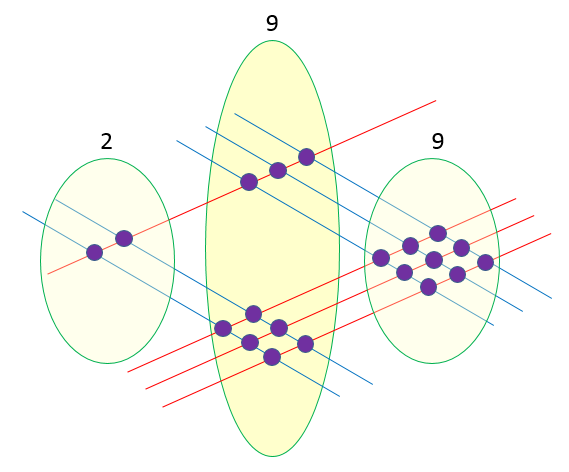
This diagram is a little bit more complete than the other one, and represents multiplication of 23 x 13.
It doesn’t matter which number you start with, but you need to lie the sticks down starting from the left, so in this case the leftmost red line represents the 1 and of the rightmost 3 red lines represent the 3 in 13. Likewise the 2 blue lines represent the 2 in 23 and further to the right (and indeed slightly above) these 3 blue lines represents the 3 in 23.
Starting from the left we can see that there are 2 intersections, in the middle we have a total of 9 intersections and to the right we have another 9. Our result is therefore 299.
We can also move on to larger numbers, each number including 3 or more digits. This does make the “laying out of the sticks” a little bit more cumbersome but the result is worked out in exactly the same way.