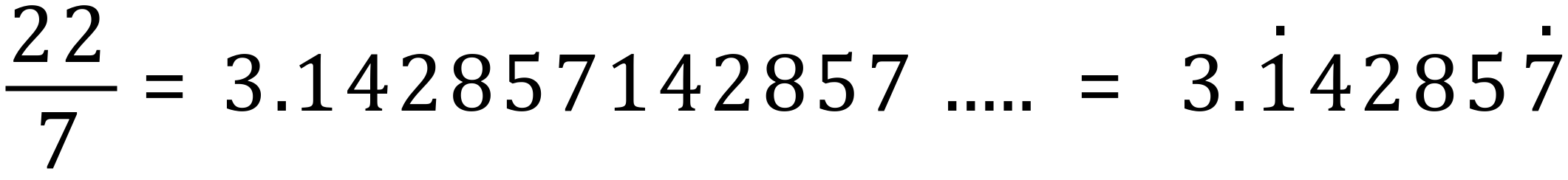Displaying Repeating Decimals
As the image below might suggest, repeating decimals will extend to the right of the decimal point infinitely. There are a couple of ways to display this so as to avoid having to write out a laborious, infinitely long sequence of repeating numbers, which would be totally pointless at least, and almost certainly prone to transcription errors, so why bother?

One such method, as the cartoon suggests is to put a small horizontal bar above the number which is to repeat. In the case of the cartoon the decimal would be 0.8333333...... with the number three repeating indefinitely to the right .
You are more likely to see the "dot" method and its applications in British mathematics books. We will now take a look at a couple of numbers which are repeating, and show how the repeated sections can be demonstrated.
Example 1: The irrational number "Pi" (two representations, only one can utilise the "dot" method).
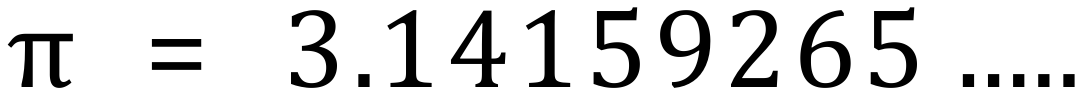
This particular version of pi is a truly irrational number, the decimal part extends infinitely to the right but there is no pattern in the numbers. This is a case where a repeating (infinite) decimal cannot be shortened using the dot method, it can only be shortened by rounding to a certain number of decimal places.
Another version of pi, was quite popular in the 1960s and 1970s secondary school mathematics, given as an improper fraction of 22÷7. If you put this into a calculator you will produce the following number:
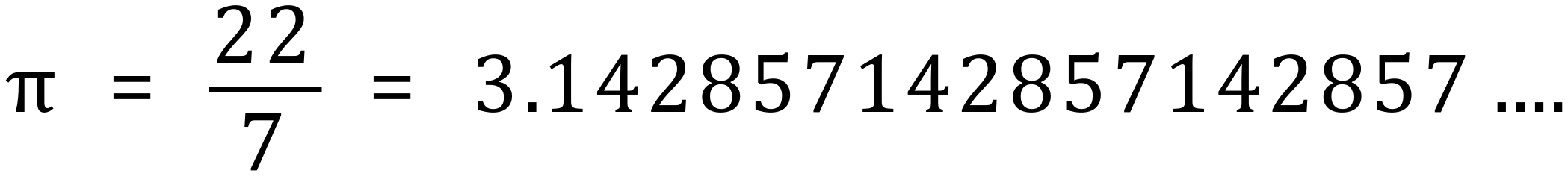
If you study this number you should be up to see that there are six decimal numbers in a constantly repeating block. "142857" repeats infinitely to the right.
If you have a single repeating infinite number, this is very easily shown in the dot notation, for example the fraction two thirds is shown like this:
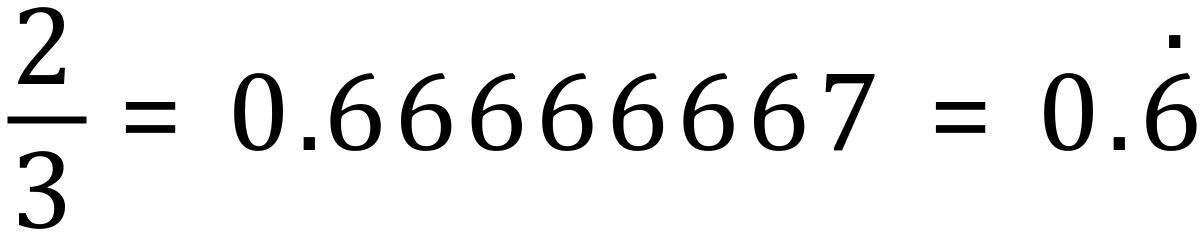
If you have a number with 2 repeating decimals, such as for example the fraction 45÷99, you would show it like this:
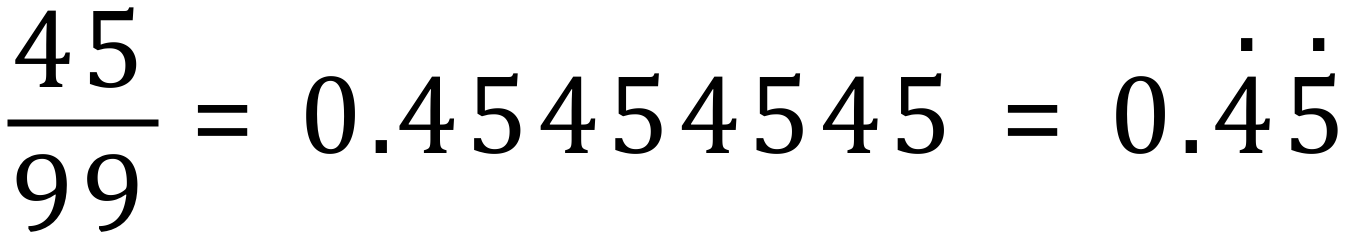
Finally, a number such as our 1960s/1970s improper fraction version of pi would be written like this, with just the boundary values of the repeating block highlighted using dots: