Irrational Numbers
Perhaps rather obviously, any number declared not to be rational is irrational. Just as we stated that rational numbers can be shown as, say, fractions eg: 1/2 the irrational numbers cannot be represented this way.
An irrational number usually has an infinitely long, non repeating decimal part. For example the solution to the Pythagoras Theorem problem posed by the right angled triangle with side length =1 producing a hypotenuse of "root 2":
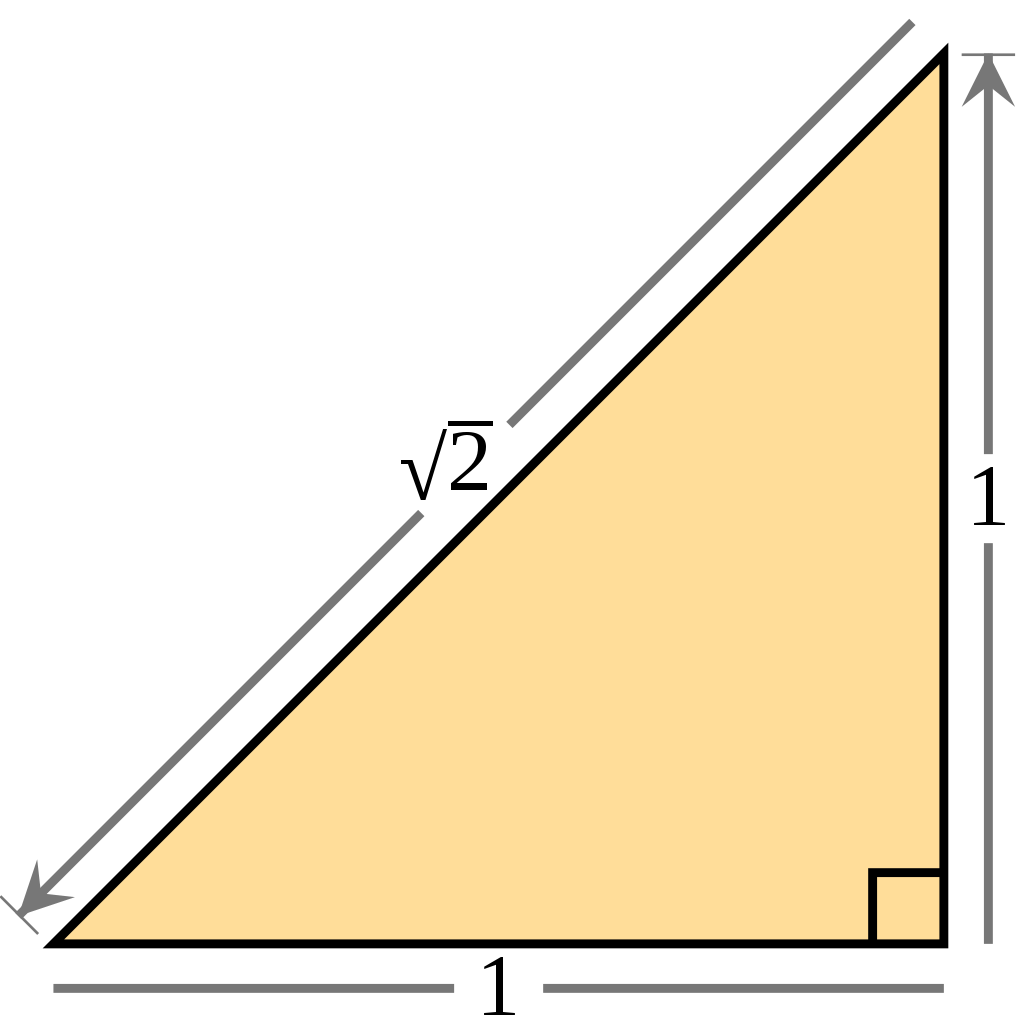
The exact length of the hypotenuse IS the square root of 2, ie: the value left as a "surd", not 1.414....... as the decimal part is infinite and non repetitive. This is an interesting concept as we have another irrational number that we meet frequently in mathematics, our old friend "pi" which represents the ratio of the circumference of a circle to its diameter (or radius):
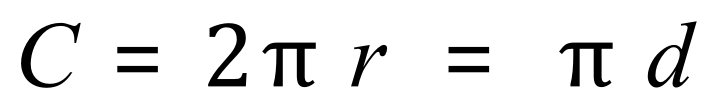
When you first start to study circles, you will be asked to calculate the circumference of a circle and you will be given a value for (usually) the radius, from this you will enter the radius into the first part of the equation shown, multiply by pi then multiply by two to arrive at your answer. Of course you need to be given a value for pi and you will usually find this contained at the end of the question:
"Calculate the circumference of a circle with a radius equal 3 cm (take pi to be 3.142)".
I don't want you to really do this calculation (unless you want to, after all who am I to to stifle your mathematical enthusiasm :-)) but rather to show the difference between the irrational version of pi and the rational version of pi. In this particular question you are given the first three decimal places of the irrational version of pi, this particular version does extend infinitely and is an ideal second example of an irrational number (in fact it has been calculated to over 1 trillion decimal places).
There is another version of pi which was quite popular in secondary school mathematics in the 1960s and 1970s, represented as an improper fraction:

Calculator version = 3.1428571428571428571428571428571...
This version of pi does have the decimal part stretching to infinity, but it is repetitive. If you examine it you will see that six decimal places repeat infinitely so this makes this particular version of pi a rational number because it can be represented as a fraction:
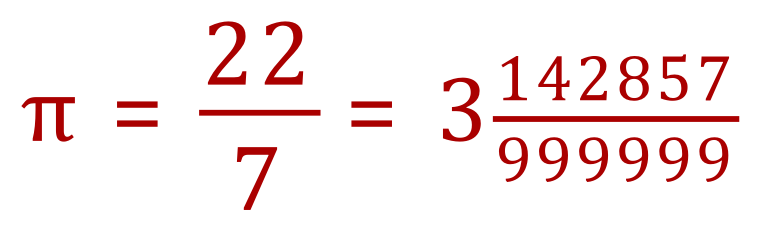
Not a particularly easy thing to say that this particular version of pi is "22/7" or "3 and 142,857 / 999,999 ths".