Elastic Potential Energy
Stretching an object, or squashing it can transfer energy to that objects "elastic" potential energy store. There are a number of factors to consider here, how strong the object, often a spring, is and how far it has been stretched or compressed. The formula to calculate the elastic potential energy is not unlike the formula used for kinetic energy, but of course contains different variables.
Formula to calculate the elastic potential energy (in Joules) of a spring is given by:
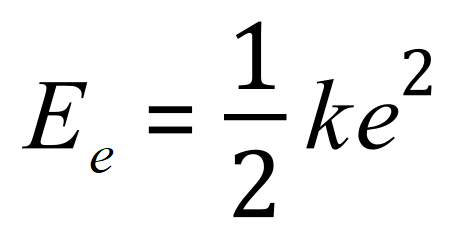
Where 'Ee' is the elastic potential energy, 'k' is the spring constant in newtons per metre and 'e' is the extension/compression applied in metres.
Q. A spring with a spring constant of 65 N per metre is stretched from its normal length of 10 cm to a length of 47 cm. Calculate the elastic potential energy in its elastic potential energy store.
A. Questions like this usually start off with straightforward "plug and go" but you may not be that lucky all the time, in this particular case you have all the information you need and can simply substitute it into the equation:
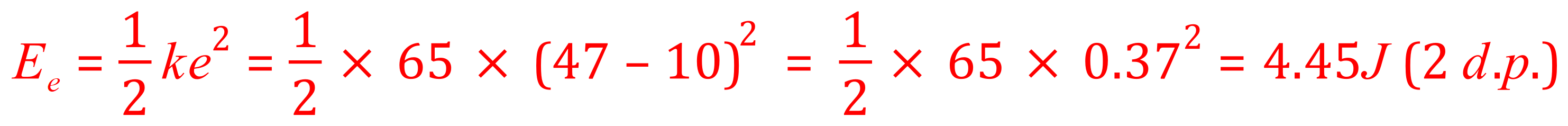
An important thing to note here is the fact that I have explained the extension fully by originally enclosing it in parentheses. The reason I have made it this obvious is that 'e' refers to an extension and is not a final length, also if you work the equation from left to right you will see that initially I quoted the final length and starting length in centimetres (47-10) but converted the answer immediately into metres by dividing by 100. This is why the value being squared is 0.37 and not simply 37.
I said previously that you will not necessarily just be given values to plug into an equation, you may be given a little bit of "preparatory" work such as converting units and/or rearranging equations before you can actually go ahead and answer the question. Let's take a look at another example where this is the case.
Q. A spring is stretched by 60 cm which transfers 36 J of energy into its elastic potential energy store. Calculate, from this data, the spring constant in newtons per metre.
A. There are two little "preparatory" problems to take care of, first of all you are given a measurement in centimetres which needs to be converted into metres and also the equation for the elastic potential energy has to be rearranged to make the spring constant 'k' the subject.
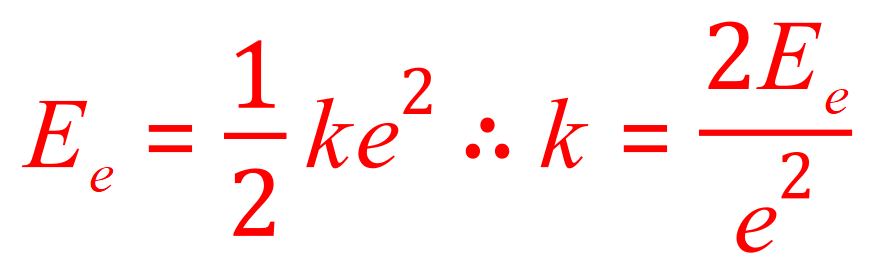
This is the rearrangement, before we start looking at putting in numbers take a look at the value you have been given for the extension. You've been given 60 cm which is 0.6 m but note that this is an extension not a final length, so you have nothing to subtract from this as this is the value that you would have obtained had you been given starting and finishing values anyway. So in this particular case we can use the value 60 cm which as I stated previously is 0.6 m.
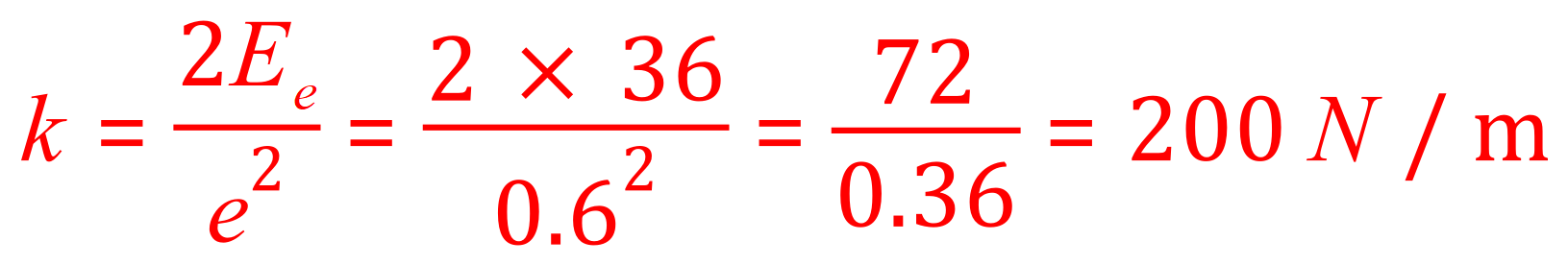
Q. A spring with a spring constant of 65 N per metre is stretched to length of 47 cm. At this point the elastic potential energy store contains 4.45 J of energy. How long is the spring when it is at rest?
A. This is simply a restatement of the first question, but phrased in such a way as to make you really think about your mathematical skills. The "at rest" length is simply the starting length before the extension is applied. We are told in the question that the spring is stretched to 47 cm but we are not told how long it was to start with, this is the whole idea of the question:
Represented mathematically this is what the question is asking you:
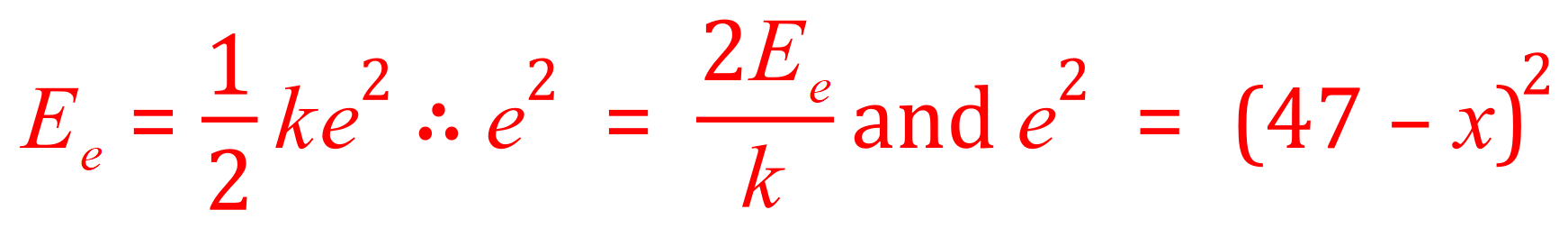
You are being asked to find the value of 'x'. Let's put some values into the equation now that we have rearranged it in terms of 'e' squared:

One more tap on the calculator will give us a value for 'e' but notice that I've deliberately used the full calculator value until I am ready to present a final answer. It is worthy of note at this point that the final answer which I'm expecting (10) will be slightly different because I am using a rounded value for the energy, 4.45 Joules.

We can now also state (remembering that 47cm must be converted to 0.47m):

Rearranging this:

Using the calculator value for E (4.44925) would have returned exactly 0.1m as the answer.