Forces and Elasticity (Hooke's Law)
In a previous section we looked at the storage of elastic potential energy in a compressed or expanded spring or otherwise elastic item. We used a fairly straightforward formula, which doesn't look unlike the formula for kinetic energy, to calculate the amount of energy in Joules held in the elastic potential energy store, what we didn't cover was the background physics behind this. We are now going to cover this by reference to forces and elasticity and introduce Hooke's Law.
>> Elastic Potential Energy <<
There are certain terms to learn in this section, for example if we stretch an item but upon releasing it, the item returns to its normal shape then it is said to have been "elastically deformed". If, however we stretch an item but it is unable to return to its normal form (it has been overstretched) we say that it as being "inelastically deformed".
To put it bluntly, if we inelastically deform a spring, it's ruined!. This is particularly relevant when we come to the practicals as the investigation requires us to add successive amounts of force to a spring, and it is easily overdone.
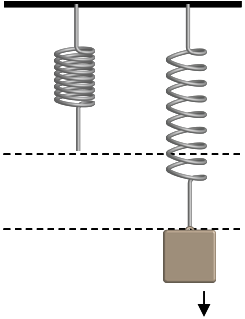
Look at the picture. The spring on the left is in its normal "at rest" state with no load applied to it, in other words there are no downward forces acting on the spring. The picture on the right shows the same spring with a force being applied to it, and the dotted lines represent the overall extension that the spring has experienced because of the force.
The extension of the spring is directly proportional to the force applied, so the more we increase the force the more the spring will extend (or compress if we are doing it that way). However, there is a limit that we must not exceed to avoid inelastic deformation of the spring. If we pass that point the spring will not return to its normal shape and will be ruined.
So, what we know so far is this:
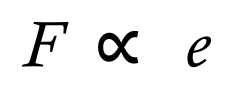
This is simply a scientific way of saying that the force is proportional to the extension, or rather the extension is proportional to the force applied. We introduce a concept known as the "spring constant" to remove the proportionality and make an equation out of this expression. The spring constant is defined as "k" and is measured in newtons per metre. The higher the spring constant, the stronger the spring and of course the converse applies.
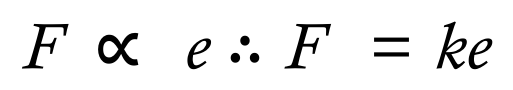
Where "F" denotes the force applied (in Newtons), "k" is the spring constant with units of Newtons per metre, and "e" extension (or compression) measured in metres. Usually in questions concerning springs, you will be given two out of three variables and asked to calculate the remaining one.
Example:
A spring at rest has a length of 23.2 cm. A steel ball bearing is suspended from the spring, which then extends to an overall length of 25.1 cm. Given that the spring constant "k" is 60 N per metre, calculate the weight (in Newtons) of the ball bearing.
This is a perfect example of what I mentioned previously, you are given values for "k" and "e" but you need to make sure that these are in the correct units. Straight away you should be able to see the extension has been given in centimetres, but the calculations require this to be converted to metres.
Extension is therefore (25.1 - 23.2) = 1.9cm = 0.019m. we can now "plug" these values into the equation to calculate the force being applied to the spring, in other words the weight (in Newtons) of the ball bearing.
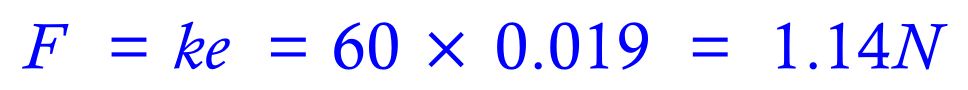
Remember the difference between "mass" and "weight", mass is the "amount of substance" and weight is a measure of the effect of the acceleration due to gravity on an object's mass. In other words mass never changes, but weight can depending on the acceleration due to gravity.
Example:
A 48 Newton Force is used to compress a spring with a spring constant of 192 N per metre. Calculate the compression of the spring given this information.
Once again this is the typical type of question, you are given two of the variables, and you're expected to calculate the value of the remaining one. This is simply a rearrangement of the above equation in terms of the unknown value, which in this case is "e":
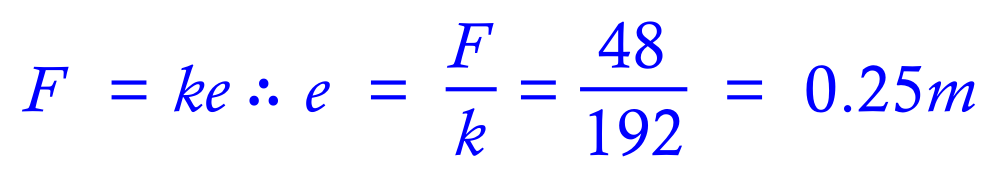
>> Questions <<
>> Limit of Proportionality <<