Looking at the Equilateral Triangle, is quite easy to see that the internal angle is 60°, similarly with the Square 90° and even with the Pentagon 108°.  These are quite easy to memorise but the same cannot easily said to be the case if you wish to work out for example the internal angle of a 14 sided shape, or a 27 sided shape.  Fortunately, the purity of mathematics often offers us a shortcut in the form of a rule, or formula for this.


Let us call the number of sides of the polygon “N”


We have already seen that the external angles, irrespective of how many of them there are, always seem to add up to 360° and we can use this fact to our advantage in deducing our formula.  We can arrive at the external angle quite simply by dividing three hundred and sixty by the number of sides:



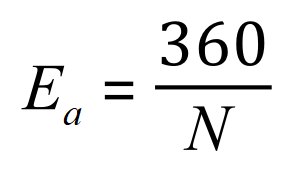
And since the internal and external angles are supplementary (that is both add up to180 °) we can see that the internal angle must be 180° minus the external angle:

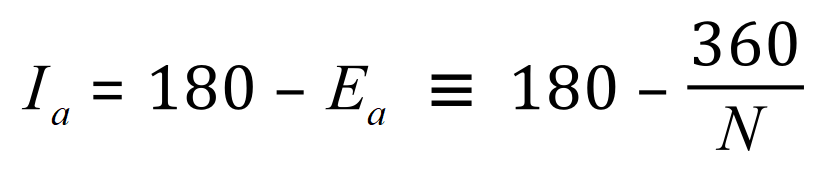
Let us take a look at a couple of obvious examples and then we will take a look at some that are not quite so straightforward:


1. The external angle of an Equilateral Triangle is 120°:




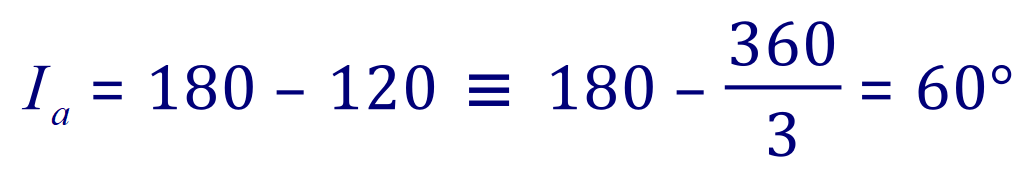
So the internal angle of an equilateral triangle is of course 60°


2.  The external angle of a Square is 90°:




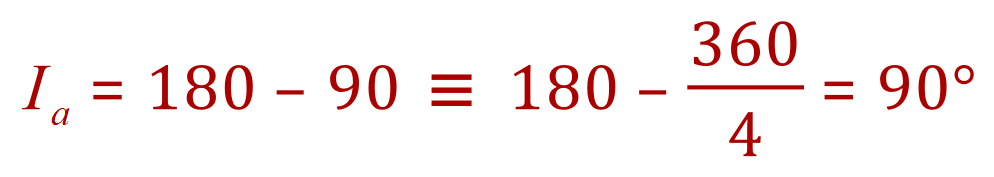
So the internal angle of the Square is also 90° (this is the only occasion where internal and external are the same).


3.  The external angle of an Octagon is 45°:




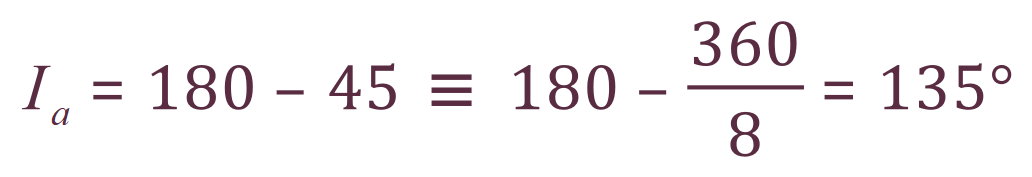
So the internal angle of the Octagon must be 135°


4.  What is the internal angle of a Nonagon (9 sided shape)?



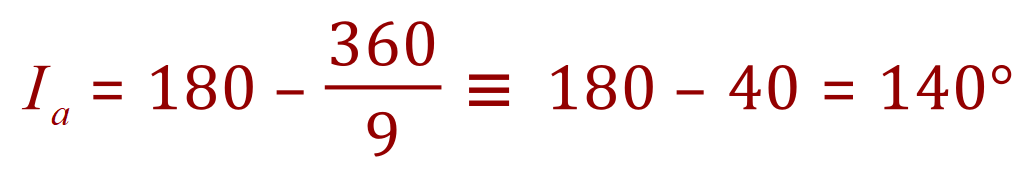
The internal angle of a Nonagon is therefore 140°


5.  What is the internal angle of a Heptacontakaidigon (72 sided shape)?



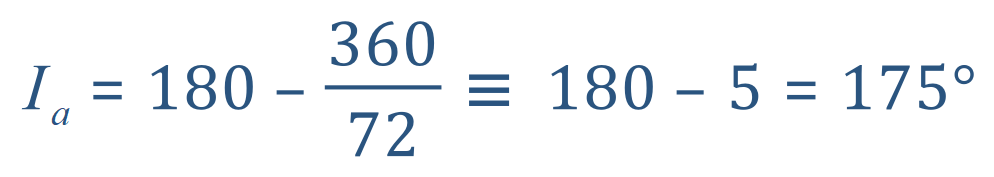
The internal angle of this shape is therefore 175° and given our previous argument about high values of N it would look very circular indeed!